吉林省长春市宽城区2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 实数a在数轴上的对应点的位置如图所示.若 , 则b的值可以是( )
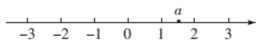 A、 B、0 C、1 D、22. 太阳的体积约为1400000000000000000立方千米,将1400000000000000000这个数用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个相同的小正方体组成的立体图形,这个立体图形的左视图是( )
A、 B、0 C、1 D、22. 太阳的体积约为1400000000000000000立方千米,将1400000000000000000这个数用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个相同的小正方体组成的立体图形,这个立体图形的左视图是( )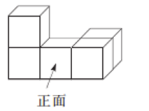 A、
A、 B、
B、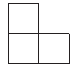 C、
C、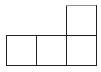 D、
D、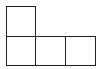 4. 不等式组的解集是( )A、 B、 C、 D、无解5. 将一副三角尺(厚度不计)如图摆放,使有刻度的两条边互相平行,则图中的大小为( )
4. 不等式组的解集是( )A、 B、 C、 D、无解5. 将一副三角尺(厚度不计)如图摆放,使有刻度的两条边互相平行,则图中的大小为( ) A、 B、 C、 D、6. 如图,某数学活动小组要测量校园内旗杆的高度,点B、C在同一条水平线上,测角仪在D处测得旗杆最高点A的仰角为 . 若测角仪 , , 则旗杆的高度为( )
A、 B、 C、 D、6. 如图,某数学活动小组要测量校园内旗杆的高度,点B、C在同一条水平线上,测角仪在D处测得旗杆最高点A的仰角为 . 若测角仪 , , 则旗杆的高度为( ) A、 B、 C、 D、7. 如图,是的直径,是弦,垂直于过点C的切线,垂足为点D.若 , 则的大小为( ).
A、 B、 C、 D、7. 如图,是的直径,是弦,垂直于过点C的切线,垂足为点D.若 , 则的大小为( ). A、 B、 C、63° D、8. 如图,在平面直角坐标系中,函数( , )的图象经过A、B两点.连结、 , 过点A作轴于点C,交于点D.若 , , 则k的值为( )
A、 B、 C、63° D、8. 如图,在平面直角坐标系中,函数( , )的图象经过A、B两点.连结、 , 过点A作轴于点C,交于点D.若 , , 则k的值为( ) A、2 B、 C、4 D、
A、2 B、 C、4 D、二、填空题
-
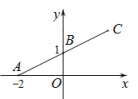
9. 分解因式: .10. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .11. 如图,在平面直角坐标系xOy中,点 , 点 . 将线段BA绕点B旋转180°得到线段BC,则点C的坐标为 .
 12. 如图,在中, . 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F.若 , 则的大小是度.
12. 如图,在中, . 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F.若 , 则的大小是度.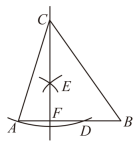 13. 如图,是等边的外接圆.若 , 则的长是(结果保留).
13. 如图,是等边的外接圆.若 , 则的长是(结果保留).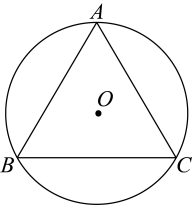 14. 在平面直角坐标系中,点、在抛物线上.当时,抛物线上A、B两点之间(含A、B两点)的图像的最高点的纵坐标为3,则m的值为 .
14. 在平面直角坐标系中,点、在抛物线上.当时,抛物线上A、B两点之间(含A、B两点)的图像的最高点的纵坐标为3,则m的值为 .三、解答题
-
15. 先化简,再求值: , 其中 .16. 某校学生会在同学中招募志愿者作为校庆活动讲解员,并设置了“A(即兴演讲)B(朗诵短文)、C(电影片段配音)”这三个测试项目,报名的同学通过抽签的方式从这三个项目中随机抽取一项进行测试.甲、乙两位同学报名参加了测试,请用画树状图(或列表)的方法,求这两位同学恰好都抽到A(即兴演讲)测试项目的概率.17. 某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木.该活动开始后,实际每天比原计划每天多植树50棵,实际植树600棵所需时间与原计划植树450棵所需时间相同,求实际每天植树的棵数.18. 图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B、C均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,不要求写出画法.
 (1)、在图①中作的角平分线 .(2)、在图②、图③中,过点C作一条直线 , 使点A、B到直线的距离相等,图②、图③所画直线不相同.19. 如图,在四边形中,对角线与相交于点O,垂直平分 , 点E是上一点,且 .
(1)、在图①中作的角平分线 .(2)、在图②、图③中,过点C作一条直线 , 使点A、B到直线的距离相等,图②、图③所画直线不相同.19. 如图,在四边形中,对角线与相交于点O,垂直平分 , 点E是上一点,且 .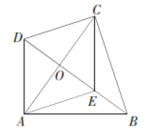 (1)、求证:四边形是菱形.(2)、若点E是的中点, , , 则的值为 .20. 为整体提升学生的综合素质,某中学利用课后服务时间,对七年级300名学生全员开设了A、B、C三类课程.经过一个学期的课程学习,学校想了解学生课程学习的效果,从中随机抽取20名学生进行了检测.这三类课程的成绩均为百分制,抽取的20名学生A、B、C三类课程的成绩情况统计图如下:
(1)、求证:四边形是菱形.(2)、若点E是的中点, , , 则的值为 .20. 为整体提升学生的综合素质,某中学利用课后服务时间,对七年级300名学生全员开设了A、B、C三类课程.经过一个学期的课程学习,学校想了解学生课程学习的效果,从中随机抽取20名学生进行了检测.这三类课程的成绩均为百分制,抽取的20名学生A、B、C三类课程的成绩情况统计图如下: (1)、例如:学生甲A类课程的成绩是60分,则该生B类课程的成绩是80分,C类课程的成绩是80分.
(1)、例如:学生甲A类课程的成绩是60分,则该生B类课程的成绩是80分,C类课程的成绩是80分.①学生乙A类课程的成绩是98分,则该生C类课程的成绩是分.
②学生丙C类课程的成绩是45分,则该生三类课程的平均成绩是分.
(2)、在图③中补全这20名学生B类课程成绩的频数分布直方图.(数据分成7组: , , , , , , )
(3)、学校规定成绩在85分及以上为优秀,估计该校七年级学生A类课程成绩优秀的人数.21. 装有一个进水管和一个出水管的容器,开始时,先打开进水管注水,6分钟时,再打开出水管排水,16分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示. (1)、进水管注水的速度为升/分钟.(2)、当时,求y与x之间的函数关系式.(3)、求a的值.22.
(1)、进水管注水的速度为升/分钟.(2)、当时,求y与x之间的函数关系式.(3)、求a的值.22. (1)、【问题原型】如图①,在 , , , 求点C到的距离.(2)、【问题延伸】如图②,在 , , . 若点M在边上,点P在线段上,连结 , 过点P作于Q,则的最小值为 .(3)、【问题拓展】如图(3),在矩形中, . 点E在边上,点M在边上,点F在线段上,连结 . 若 , 则的最小值为 .23. 如图,在中, , , 点D为边的中点.点P从点C出发以每秒1个单位的速度沿向终点B运动.以为边作正方形 , 点N在边上.设点P的运动时间为t秒().
(1)、【问题原型】如图①,在 , , , 求点C到的距离.(2)、【问题延伸】如图②,在 , , . 若点M在边上,点P在线段上,连结 , 过点P作于Q,则的最小值为 .(3)、【问题拓展】如图(3),在矩形中, . 点E在边上,点M在边上,点F在线段上,连结 . 若 , 则的最小值为 .23. 如图,在中, , , 点D为边的中点.点P从点C出发以每秒1个单位的速度沿向终点B运动.以为边作正方形 , 点N在边上.设点P的运动时间为t秒().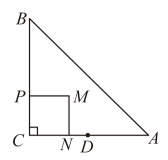 (1)、用含t的代数式表示线段的长.(2)、连接 , 则度;当点D与点M的距离最短时,线段的长为 .(3)、连接 , 当将正方形的面积分为3:5两部分时,求t的值.(4)、作点C关于直线的对称点 , 当点、点M到的某一条直角边所在直线距离相等时,直接写出t的值.24. 在平面直角坐标系中,抛物线经过点和点 . 点P在直线上运动(点P不与点A、B重合),过点P作y轴的平行线,交抛物线于点Q.设点P的横坐标为m.(1)、求这条抛物线所对应的函数表达式.(2)、求线段的长.(用含m的代数式表示)(3)、以为边作矩形 , 使轴,且点N的横坐标为 .
(1)、用含t的代数式表示线段的长.(2)、连接 , 则度;当点D与点M的距离最短时,线段的长为 .(3)、连接 , 当将正方形的面积分为3:5两部分时,求t的值.(4)、作点C关于直线的对称点 , 当点、点M到的某一条直角边所在直线距离相等时,直接写出t的值.24. 在平面直角坐标系中,抛物线经过点和点 . 点P在直线上运动(点P不与点A、B重合),过点P作y轴的平行线,交抛物线于点Q.设点P的横坐标为m.(1)、求这条抛物线所对应的函数表达式.(2)、求线段的长.(用含m的代数式表示)(3)、以为边作矩形 , 使轴,且点N的横坐标为 .①当矩形的面积被坐标轴平分时,求m的值.
②当矩形的周长随m的增大而增大,且矩形的边与抛物线有两个交点时,直接写出m的取值范围.