吉林省松原市前郭尔罗斯蒙古族自治县2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 的倒数为( )A、 B、 C、4 D、2. 下列几何体的主视图既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 关于x的一元二次方程没有实数根,则k的取值范围是( )A、 B、 C、 D、4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
3. 关于x的一元二次方程没有实数根,则k的取值范围是( )A、 B、 C、 D、4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( ) A、10° B、15° C、20° D、30°5. 化简的结果是( )A、 B、 C、 D、6. 关于二次函数 的最大值或最小值,下列说法正确的是( )A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6
A、10° B、15° C、20° D、30°5. 化简的结果是( )A、 B、 C、 D、6. 关于二次函数 的最大值或最小值,下列说法正确的是( )A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6二、填空题
-
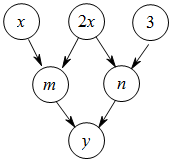
7. 分解因式:a2-9b2=;8. 关于x的方程的解是 .9. 不等式 的解集是 .10. 点在一次函数的图像上,当时, , 则a的取值范围是 .11. 在 中, , 为BC边上的高, ,则BC的长为 .12. 如图,约定:上方相邻两数之和等于这两个数下方剪头共同指向的数.示例:即4+3=7,则y= .
 13. 如图,在 △ABC中, ∠ACB=90° , D,E,F分别为AB,BC,CA的中点.若EF的长为10,则CD的长为 .
13. 如图,在 △ABC中, ∠ACB=90° , D,E,F分别为AB,BC,CA的中点.若EF的长为10,则CD的长为 .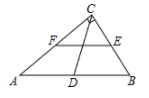 14. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.
14. 在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做将矩形窗框分为上下两部分,其中E为边的黄金分割点,即.已知为2米,则线段的长为米.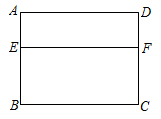 15. 计算: .
15. 计算: .三、解答题
-
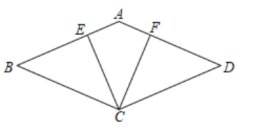
16. 如图,四边形是菱形,点E,F分别在上, . 求证 .
 17. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回搅匀,再从中随机摸出一个小球记下标号.规定当两次摸出的小球标号相同时中奖,求中奖的概率,请用画树状图或列表法的方法求中奖的概率.18. 如图,AB是⊙O的直径,PB是⊙O的切线,连接AP交⊙O于点C。点D在⊙O上,∠CDB=45°,求证:AB=BP。
17. 九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回搅匀,再从中随机摸出一个小球记下标号.规定当两次摸出的小球标号相同时中奖,求中奖的概率,请用画树状图或列表法的方法求中奖的概率.18. 如图,AB是⊙O的直径,PB是⊙O的切线,连接AP交⊙O于点C。点D在⊙O上,∠CDB=45°,求证:AB=BP。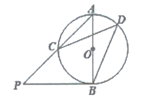 19. 如图,同学们利用所学知识去测量三江源某河段某处的宽度 小宇同学在A处观测对岸点C,测得 ,小英同学在距点A处60米远的B点测得 ,请根据这些数据算出河宽 精确到 米, , .
19. 如图,同学们利用所学知识去测量三江源某河段某处的宽度 小宇同学在A处观测对岸点C,测得 ,小英同学在距点A处60米远的B点测得 ,请根据这些数据算出河宽 精确到 米, , . 20. 某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.
20. 某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试,各项满分均为10分,成绩高者被录用.图1是甲、乙测试成绩的条形统计图.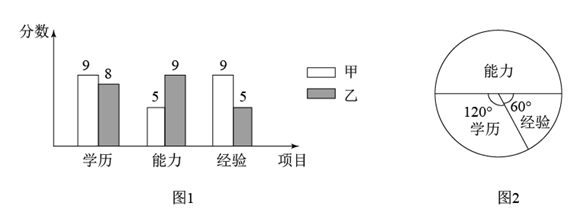 (1)、分别求出甲、乙三项成绩之和,并指出会录用谁;(2)、若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.21. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),
(1)、分别求出甲、乙三项成绩之和,并指出会录用谁;(2)、若将甲、乙的三项测试成绩,按照扇形统计图(图2)各项所占之比,分别计算两人各自的综合成绩,并判断是否会改变(1)的录用结果.21. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),①求函数y1 , y2的表达式:
②当2<x<3时,比较y1与y2的大小(直接写出结果).
(2)、若点C(2,n)在函数y1的图象上,点C先向下平移2个单位,再向左平移4个单位,得点D,点D恰好落在函数y1的图象上,求n的值,22. 如图,3×3正方形网格中,每个小正方形的顶点称为格点,点A,B都在格点上,以线段为边,按下列要求画四边形 , 使得点C,D都在格点上.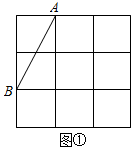
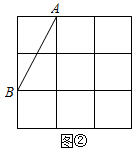
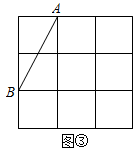 (1)、图①中的四边形是轴对称图形,但不是中心对称图形(2)、图②中的四边形是中心对称图形,但不是轴对称图形(3)、图③中的四边形既是中心对称图形,也是轴对称图形23. 如图,在中, , 为边上一动点, , 垂足为N.设A,M两点间的距离为xcm(),B,N两点间的距离为ycm(当M点和B点重合时,B,N两点间的距离为0).
(1)、图①中的四边形是轴对称图形,但不是中心对称图形(2)、图②中的四边形是中心对称图形,但不是轴对称图形(3)、图③中的四边形既是中心对称图形,也是轴对称图形23. 如图,在中, , 为边上一动点, , 垂足为N.设A,M两点间的距离为xcm(),B,N两点间的距离为ycm(当M点和B点重合时,B,N两点间的距离为0).
小明根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
(1)、列表:下表的已知数据是根据A,M两点间的距离x进行取点、画图、测量,分别得到的y与x的几组对应值:x/cm
0
0.5
1
1.5
1.8
2
2.5
3
3.5
4
4.5
5
y/cm
4
3.96
3.79
3.47
a
2.99
2.40
1.79
1.23
0.74
0.33
0
请你通过计算,补全表格:a=;
(2)、描点、连线:在平面直角坐标系中,描出表中各组数值所对应的点(x,y),并画出y关于x的函数图象;(3)、探究性质:随着自变量x的不断增大,函数y的变化趋势: .24. 已知等边三角形ABC,过A点作AC的垂线l,点P为l上一动点(不与点A重合),连接CP,把线段CP绕点C逆时针方向旋转60°得到CQ,连QB.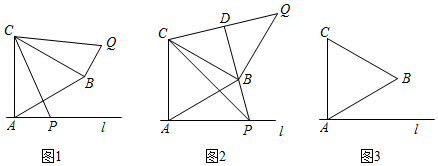 (1)、如图1,判断线段AP与BQ的数量关系,并说明理由;(2)、如图2,当点P、B在AC同侧且AP=AC时,求证:直线PB垂直平分线段CQ;(3)、如图3,若等边三角形ABC的边长为4,点P、B分别位于直线AC异侧,且△APQ的面积等于 , 请直接写出线段AP的长度.25. 如图,在正方形ABCD中,AB=2,连接AC。P,Q两点分别从A,D同时出发,点P以每秒1个单位长度的速度沿线段AB向终点B运动;点Q沿折线D→A→C向终点C运动,在DA上的速度为每秒2个单位长度,在AC上的速度为每秒2 个单位长度。在运动过程中,以AP,AQ为邻边作平行四边形APMQ。设运动时间为x秒,平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。
(1)、如图1,判断线段AP与BQ的数量关系,并说明理由;(2)、如图2,当点P、B在AC同侧且AP=AC时,求证:直线PB垂直平分线段CQ;(3)、如图3,若等边三角形ABC的边长为4,点P、B分别位于直线AC异侧,且△APQ的面积等于 , 请直接写出线段AP的长度.25. 如图,在正方形ABCD中,AB=2,连接AC。P,Q两点分别从A,D同时出发,点P以每秒1个单位长度的速度沿线段AB向终点B运动;点Q沿折线D→A→C向终点C运动,在DA上的速度为每秒2个单位长度,在AC上的速度为每秒2 个单位长度。在运动过程中,以AP,AQ为邻边作平行四边形APMQ。设运动时间为x秒,平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。
 (1)、当点M在BC上时,x=(2)、求y关于x的函数解析式,并写出x的取值范围;(3)、连接MB,当0°<∠MBP<90°时,直接写出tan∠MBP= 时x的值。26. 已知抛物线 .
(1)、当点M在BC上时,x=(2)、求y关于x的函数解析式,并写出x的取值范围;(3)、连接MB,当0°<∠MBP<90°时,直接写出tan∠MBP= 时x的值。26. 已知抛物线 . (1)、如图①,若抛物线图象与x轴交于点 , 与y轴交点 . 连接 .
(1)、如图①,若抛物线图象与x轴交于点 , 与y轴交点 . 连接 .①求该抛物线所表示的二次函数表达式;
②若点P是抛物线上一动点(与点A不重合),过点P作轴于点H,与线段交于点M.是否存在点P使得点M是线段的三等分点?若存在,请求出点P的坐标;若不存在,请说明理由.
(2)、如图②,直线与y轴交于点C,同时与抛物线交于点 , 以线段为边作菱形 , 使点F落在x轴的正半轴上,若该抛物线与线段没有交点,求b的取值范围.