吉林省吉林市2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 中国是世界上最早使用负数的国家,战国时期李悝所著的《法经》中已使用负数.如果公元前500年记作年,那么公元2023年应记作( )A、年. B、年. C、年. D、年.2. 如图是由4个相同小正方体组成的几何体,其三视图中面积最大的是( )
 A、主视图 B、左视图 C、俯视图 D、三视图的面积相等3. 下列运算正确的是( )A、 B、 C、 D、4. 斑马线的作用是为了引导行人安全地通过马路.某数学兴趣小组为了验证斑马线是由若干条平行线组成的,在保证安全的前提下,按照如图方式分别测出 , 这种验证方法的数学依据是( )
A、主视图 B、左视图 C、俯视图 D、三视图的面积相等3. 下列运算正确的是( )A、 B、 C、 D、4. 斑马线的作用是为了引导行人安全地通过马路.某数学兴趣小组为了验证斑马线是由若干条平行线组成的,在保证安全的前提下,按照如图方式分别测出 , 这种验证方法的数学依据是( ) A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、内错角相等,两直线平行 D、同旁内角互补,两直线平行5. 在学习有序数对时,老师和同学们用如图所示的密码表玩听声音猜动物的游戏.当听到“叮叮-叮,叮叮叮-叮叮,叮-叮”时,分别对应的字母是“C,A,T”,表示的动物是猫.当听到“叮叮-叮叮,叮-叮叮叮,叮叮叮-叮”时,表示的动物是( )
A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、内错角相等,两直线平行 D、同旁内角互补,两直线平行5. 在学习有序数对时,老师和同学们用如图所示的密码表玩听声音猜动物的游戏.当听到“叮叮-叮,叮叮叮-叮叮,叮-叮”时,分别对应的字母是“C,A,T”,表示的动物是猫.当听到“叮叮-叮叮,叮-叮叮叮,叮叮叮-叮”时,表示的动物是( )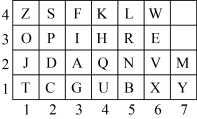 A、牛 B、鱼 C、狗 D、猪6. 图1是等边三角形铁丝框 , 按图2方式变形成以A为圆心,长为半径的扇形(图形周长保持不变),则所得扇形的圆心角的度数是( )
A、牛 B、鱼 C、狗 D、猪6. 图1是等边三角形铁丝框 , 按图2方式变形成以A为圆心,长为半径的扇形(图形周长保持不变),则所得扇形的圆心角的度数是( )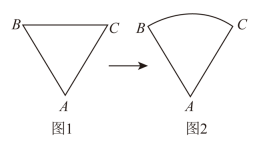 A、 . B、 . C、 . D、 .
A、 . B、 . C、 . D、 .二、填空题
-
7. 2023年全国两会在北京圆满落下帷幕.《两会微博热度报告》显示,两会相关话题信息阅读量达78200000000.数据78200000000用科学记数法表示为 .8. 因式分解: .9. 今年二月末吉林省政府免费发放第二轮冰雪消费券,王先生领了一张“逐冰戏雪券”,该券可以使票价打七折.若他凭此券在吉林市万科松花湖滑雪场购买了一张票价为a元的套票,则王先生实际花费元.10. 一元二次方程 的根的判别式的值是 .11. 五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐.如图, , , 为直线与五线谱的横线相交的三个点,则的值是.
 12. 如图,将等腰三角形纸片折叠,使底边落在腰上,展开后得到折痕 , 若 , 则 .
12. 如图,将等腰三角形纸片折叠,使底边落在腰上,展开后得到折痕 , 若 , 则 .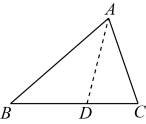 13. 如图, , 分别以A,B为圆心,长为半径画弧,两弧相交于M,N两点.连接 , 则四边形的面积为 .
13. 如图, , 分别以A,B为圆心,长为半径画弧,两弧相交于M,N两点.连接 , 则四边形的面积为 .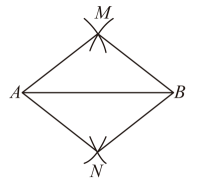 14. 如图,是等边三角形, , 若的半径为2,圆心O在线段上运动,则点A到上的点的距离最小值为 .
14. 如图,是等边三角形, , 若的半径为2,圆心O在线段上运动,则点A到上的点的距离最小值为 .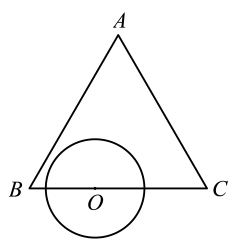
三、解答题
-
15. 先化简,再求值: , 其中 , .16. 图1是郝老师制作的风筝,图2是风筝骨架的示意图,其中 , , . 求的度数.
 17. 为了使学生树立正确的劳动观,吉林市某校在植树节当天开展劳动教育实践活动.在本次种树活动中,甲班平均每小时比乙班少种5棵树,甲班种100棵树与乙班种120棵树所用的时间相等.求乙班平均每小时种多少棵树?18. 李白是唐代伟大的浪漫主义诗人,被后人誉为“诗仙”.《春夜洛城闻笛》是他创作的一首名篇,这首古诗共有四句,如图,将这四句古诗分别制成编号为A,B,C,D的4张卡片,卡片除编号和内容外,其余完全相同.将这4张卡片背面朝上,洗匀放好.“诗圣”杜甫从4张卡片中随机抽取2张,请用列表或画树状图的方法,求出杜甫随机抽出2张卡片恰好为相邻两句古诗的概率.
17. 为了使学生树立正确的劳动观,吉林市某校在植树节当天开展劳动教育实践活动.在本次种树活动中,甲班平均每小时比乙班少种5棵树,甲班种100棵树与乙班种120棵树所用的时间相等.求乙班平均每小时种多少棵树?18. 李白是唐代伟大的浪漫主义诗人,被后人誉为“诗仙”.《春夜洛城闻笛》是他创作的一首名篇,这首古诗共有四句,如图,将这四句古诗分别制成编号为A,B,C,D的4张卡片,卡片除编号和内容外,其余完全相同.将这4张卡片背面朝上,洗匀放好.“诗圣”杜甫从4张卡片中随机抽取2张,请用列表或画树状图的方法,求出杜甫随机抽出2张卡片恰好为相邻两句古诗的概率. 19. 图1是一架三角钢琴,图2是该三角钢琴的示意图.韩老师和学生测得 , , . 求此三角钢琴最高点M到地面的距离(结果精确到).(参考数据 , , )
19. 图1是一架三角钢琴,图2是该三角钢琴的示意图.韩老师和学生测得 , , . 求此三角钢琴最高点M到地面的距离(结果精确到).(参考数据 , , ) 20. “逐梦寰宇问苍穹——中国载人航天工程三十年成就展”的成功举办,标志着我国载人航天工程正式进入空间站应用与发展阶段.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取m名学生进行测试,对成绩(百分制)进行整理、描述和分析,成绩划分为A(),B(),C(),D()四个等级,并制作出不完整的统计图如下.
20. “逐梦寰宇问苍穹——中国载人航天工程三十年成就展”的成功举办,标志着我国载人航天工程正式进入空间站应用与发展阶段.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取m名学生进行测试,对成绩(百分制)进行整理、描述和分析,成绩划分为A(),B(),C(),D()四个等级,并制作出不完整的统计图如下.
已知:B等级数据(单位:分):
80 80 81 82 85
86 86 88 89 89
根据以上信息,回答下列问题:
(1)、补全条形统计图,并填空:m= , n= .(2)、抽取的m名学生中,成绩的中位数是分,成绩不低于80分的人数占测试人数的百分比为 .(3)、这所学校共有2105名学生,若全部参加这次测试,请你估计成绩能达到A等级的学生人数.21. 一个用电器的电阻是可调节的,其范围为 . 已知电压为 , 这个用电器的电路图如图所示. (1)、功率P与电阻R有怎样的函数关系?(2)、这个用电器功率的范围是多少?22. 图1、图2、图3均是的正方形网格,每个小正方形的顶点为格点,点A,B,C均在格点上,⊙O是的外接圆,只用无刻度的直尺,按下列要求作图.
(1)、功率P与电阻R有怎样的函数关系?(2)、这个用电器功率的范围是多少?22. 图1、图2、图3均是的正方形网格,每个小正方形的顶点为格点,点A,B,C均在格点上,⊙O是的外接圆,只用无刻度的直尺,按下列要求作图. (1)、在图1中作∠BMC,使 , 且格点M在⊙O上.(2)、在图2中作∠BNC,使 , 且格点N在⊙O上.(3)、在图3中作∠PBC,使 , 且格点P在⊙O上.23. 受持续降雨影响,某水库的水位在最近内持续上涨.下表记录了这内6个时间点的水位高度,其中t表示时间,y表示水位高度.
(1)、在图1中作∠BMC,使 , 且格点M在⊙O上.(2)、在图2中作∠BNC,使 , 且格点N在⊙O上.(3)、在图3中作∠PBC,使 , 且格点P在⊙O上.23. 受持续降雨影响,某水库的水位在最近内持续上涨.下表记录了这内6个时间点的水位高度,其中t表示时间,y表示水位高度.t/h
0
1
2
3
4
5
. ..
y/m
3.00
3.05
3.10
3.15
3.20
3.25
. ..
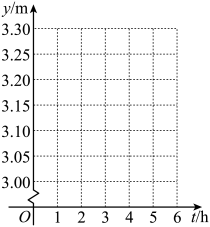 (1)、在平面直角坐标系中描出表中数据对应的点,并依次连接各点.(2)、依据水位高度y与时间t的变化规律,求符合表中数据的函数解析式.(3)、据估计这种上涨规律还会持续2h,请预测再过2h水位的高度.24. 下面是张老师数学课堂教学实践活动的一个片段:
(1)、在平面直角坐标系中描出表中数据对应的点,并依次连接各点.(2)、依据水位高度y与时间t的变化规律,求符合表中数据的函数解析式.(3)、据估计这种上涨规律还会持续2h,请预测再过2h水位的高度.24. 下面是张老师数学课堂教学实践活动的一个片段:【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作 , . 其中 , , , . 现固定三角板 , 将三角板绕点A逆时针旋转,旋转角记为 , 射线与射线交于点P,在射线上取一点Q,使 , 连接CQ.
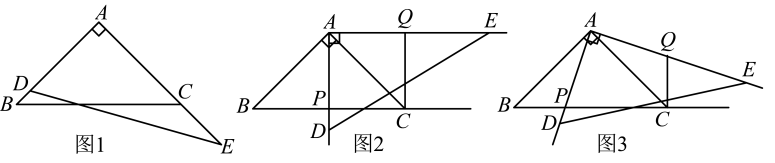 (1)、【特例探究】如图2,当时,直接写出和的数量关系和位置关系.(2)、【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.(3)、【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.(4)、【拓展应用】连接 . 若 , 的面积等于 , 请直接写出的长.25. 如图,在矩形中, , , 连接 . 点P从点A出发,沿折线A→B→C向终点C运动,在上的速度为每秒2个单位长度,在上的速度为每秒个单位长度;过点P作于点E,交线段或于点F,连接 , . 设点P运动的时间为x秒,与重合部分的图形面积为y.
(1)、【特例探究】如图2,当时,直接写出和的数量关系和位置关系.(2)、【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.(3)、【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.(4)、【拓展应用】连接 . 若 , 的面积等于 , 请直接写出的长.25. 如图,在矩形中, , , 连接 . 点P从点A出发,沿折线A→B→C向终点C运动,在上的速度为每秒2个单位长度,在上的速度为每秒个单位长度;过点P作于点E,交线段或于点F,连接 , . 设点P运动的时间为x秒,与重合部分的图形面积为y. (1)、当点P在上时,用含x的式子表示的长,并写出x的取值范围.(2)、求y关于x的函数解析式,并写出x的取值范围.(3)、当点E为的三等分点时,直接写出x的值.26. 如图,函数的图象经过点 , , .
(1)、当点P在上时,用含x的式子表示的长,并写出x的取值范围.(2)、求y关于x的函数解析式,并写出x的取值范围.(3)、当点E为的三等分点时,直接写出x的值.26. 如图,函数的图象经过点 , , . (1)、求y关于x的函数解析式.(2)、当时,求x的值.(3)、点P在函数y的图象上,其横坐标为m,将点P向右平移个单位得到点Q,连接 , 以为边向上作正方形 .
(1)、求y关于x的函数解析式.(2)、当时,求x的值.(3)、点P在函数y的图象上,其横坐标为m,将点P向右平移个单位得到点Q,连接 , 以为边向上作正方形 .①当点M在函数y的图象上时,直接写出m的取值范围.
②将函数y的图象在正方形内部(包括边界)的部分记为图象G,设图象G的最高点的纵坐标与最低点的纵坐标的和为L,直接写出时m的取值范围.