广东省雷州市2023年中考六校联考数学试卷

试卷更新日期：2023-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在实数4，0， $\frac{12}{7}$ ， $0.101$ ， $\sqrt{3}$ ， $\frac{π}{2}$ 中无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列式子正确的是（）

A、 $\sqrt[3]{- 6} = - \sqrt[3]{6}$ B、 $\pm \sqrt{16} = 4$ C、 $\sqrt{25} = \pm 5$ D、 $\sqrt{（ - 3 ）^{2}} = - 3$

查看试题解析
4. 如图， $A B$ 是 $⊙ O$ 直径， $∠ B O C = 40 °$ ，则∠D为（　　）

A、 $40 °$ B、 $30 °$ C、 $20 °$ D、 $70 °$

查看试题解析
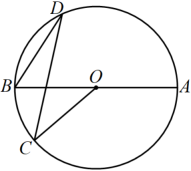5. 在《数据的分析》章节测试中，“勇往直前”学习小组6位同学的平均成绩是90，其个人成绩分别是85，95，72，100，93，a ，则这组数据的中位数和众数分别是（）

A、93，95 B、93，90 C、94，90 D、94，95

查看试题解析
6. 如图，数轴上的点A、B分别对应有理数a、b，下列结论中正确的是（）

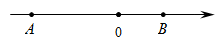A、a＞b B、|a|＞b C、－a＜b D、a＋b＞0

查看试题解析
7. 将一块三角板和一块直尺如图放置，若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数为（）

A、 $100 °$ B、 $120 °$ C、 $130 °$ D、 $140 °$

查看试题解析
8. 关于x的一元二次方程x²+4x+k=0有两个实数根，则k的取值范围是（）

A、k≤﹣4 B、k＜﹣4 C、k≤4 D、k＜4

查看试题解析
9. 某滑梯示意图及部分数据如图所示. 若 $A E = 1 m$ ，则 DF的长为（）

A、 $\frac{\tan α}{\tan β}$ B、 $\frac{\tan β}{\tan α}$ C、 $\frac{\sin β}{\sin α}$ D、 $\frac{\sin α}{\sin β}$

查看试题解析
10. 如图是二次函数y＝ax²+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y₁），（3，y₂）是抛物线上两点，则y₁＜y₂ ，其中说法正确的是（）

A、①② B、②③ C、①②④ D、②③④

查看试题解析

二、填空题

11. 计算：2sin60°-（ $\frac{1}{3}$ ）⁰＝．

查看试题解析
12. 分解因式： $4 a^{2} b - b =$ ．

查看试题解析
13. 一个正多边形的内角和等于1080°，则这个正多边形的边数等于．

查看试题解析
14. 已知张强家、体育场、文具店在同一直线上，如图的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔，然后散步走回家．图中x表示时间，y表示张强离家的距离，则下列结论不正确的是．
①张强从家到体育场用了15 $m i n$ ②体育场离文具店1.5 $k m$
③张强在文具店停留了20 $m i n$ ④张强从文具店回家用了35 $m i n$

查看试题解析
15. 如图，四位同学站成一排，按图中所示规律数数，数到2023对应的同学是．

查看试题解析

三、解答题

16. 解不等式组： ${\begin{array}{l} 2 x - 1 < 7 \\ \frac{3 x + 5}{2} - 1 \geq x \end{array}$ ，并将其解集在数轴上表示出来．

查看试题解析
17. 如图，在Rt△ABC中，∠B=90°，AB=3，BC=4．

(1)、利用尺规作线段AC的垂直平分线DE，垂足为点E，交BC于点D（保留作图痕迹，不写作法）

(2)、求△ABD的周长．

查看试题解析
18. 某校为了解九年级学生对新冠肺炎防控知识的掌握情况，从全校九年级学生中随机抽取部分学生做为样本进行调查.

根据图中提供的不完整信息，解答下列问题：

(1)、补全条形统计图，并求D类所对应扇形的圆心角的大小；

(2)、已知D类中有2名女生，从D类中随机抽取2名同学，求抽到“一男一女”的概率.

查看试题解析
19. 菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售，由于部分菜农盲目扩大种植，造成该蔬菜滞销．李伟为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的单价对外批发销售．

(1)、求平均每次下调的百分率；

(2)、小华准备到李伟处购买5吨该蔬菜，因数量多，李伟决定再给予两种优惠方案以供选择：
方案一：打九折销售；
方案二：不打折，每吨优惠现金200元．
试问小华选择哪种方案更优惠，请说明理由．

查看试题解析
20. 如图，E，F是正方形ABCD的对角线BD上的两点，且BE＝DF.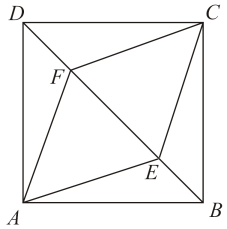

(1)、求证：△ABE≌△CDF；

(2)、若AB＝3 $\sqrt{2}$ ， BE＝2，求四边形AECF的面积.

查看试题解析
21. 如图，一次函数 $y = x + 4$ 的图像与反比例函数 $y = \frac{k}{x}$ （k为常数，且 $k \neq 0$ ）的图象交于 $A (- 1 ， a)$ ， $B (b ， 1)$ 两点．

(1)、求反比例函数的表达式；

(2)、在x轴上找一点P，使 $P A + P B$ 的值最小，求满足条件的点P的坐标；

查看试题解析
22. 如图，四边形ACBD内接于⊙O，AB是⊙O的直径，CD平分∠ACB交AB于点E，点P在AB延长线上， $∠ P C B = ∠ B D C$ ．

(1)、求证：PC是⊙O的切线；

(2)、求证： $P E^{2} = P B \cdot P A$ ；

(3)、若 $B C = 2 \sqrt{2}$ ， △ACD的面积为12，求PB的长．

查看试题解析
23. 如图一所示，在平面直角坐标中，抛物线y＝ax²+2x+c经过点A(﹣1，0）、B（3，0），与y轴交于点C，顶点为点D.在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PF $∥$ AB交BC于点F.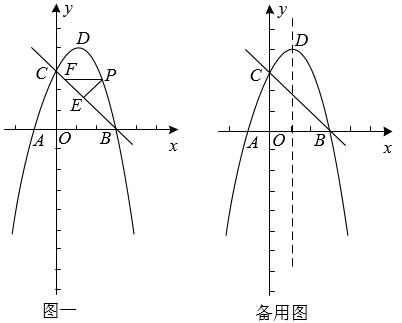

(1)、求抛物线和直线BC的函数表达式，

(2)、当△PEF的周长为最大值时，求点P的坐标和△PEF的周长.

(3)、若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由.

查看试题解析