广东省江门市新会区2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 下列各数中是无理数的是( )A、0 B、1 C、 D、2. 下列运算正确的是( )A、2a+3a=5a2 B、6m2﹣5m2=1 C、a6÷a3=a2 D、(﹣a2)3=﹣a63. 水是由氢原子和氧原子组成的,其中氧原子的直径是0.000000000074米,用科学记数法可表示为( )A、0.74×10-10米 B、74×10-12米 C、7.4×10-10米 D、7.4×10-11米4. 有5名同学,3男2女,现随机抽2人参加课外学习小组活动,其中一定抽到女同学的概率是( )A、 B、 C、 D、5. 不等式组 的解集在以下数轴表示中正确的是( )A、
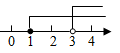 B、
B、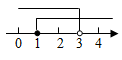 C、
C、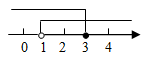 D、
D、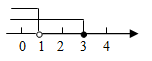 6. 如下图形是某几何体的三视图,则这个几何体是( )
6. 如下图形是某几何体的三视图,则这个几何体是( ) A、圆锥 B、圆柱 C、三棱锥 D、三棱柱7. 已知、是方程的两个实数根,则( )A、 B、 C、 D、8. 如图,在 中, 的平分线交 于点 , 的平分线交 于点 ,若 ,则 的长是( )
A、圆锥 B、圆柱 C、三棱锥 D、三棱柱7. 已知、是方程的两个实数根,则( )A、 B、 C、 D、8. 如图,在 中, 的平分线交 于点 , 的平分线交 于点 ,若 ,则 的长是( ) A、1 B、2 C、2.5 D、39. 如图,矩形OABC的面积为36,它的对角线OB与双曲线y 相交于点D , 且OD:OB=2:3,则k的值为( )
A、1 B、2 C、2.5 D、39. 如图,矩形OABC的面积为36,它的对角线OB与双曲线y 相交于点D , 且OD:OB=2:3,则k的值为( )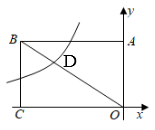 A、12 B、﹣12 C、16 D、﹣1610. 在中, , 点O是斜边边上一点,以O为圆心,为半径作圆,恰好与边相切于点D,连接 , 若 , 的半径为 , 则的长度为( )
A、12 B、﹣12 C、16 D、﹣1610. 在中, , 点O是斜边边上一点,以O为圆心,为半径作圆,恰好与边相切于点D,连接 , 若 , 的半径为 , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知方程组 ,则x+y=.12. 两位同学在描述同一反比例函数的图象时,甲同学说:“这个反比例函数图象上任意一点到两坐标轴的距离之积是”.乙同学说:“这个反比例函数图象与直线有两个交点”.你认为这两个同学所描绘的反比例函数对应的解析式是 .13. 半径为10cm的半圆围成一个圆锥,则这个圆锥的高是cm.14. 如图,是的一条半径,点P是延长线上一点,过点P作的切线 , 点B为切点.若 , , 则 .
 15. 在《九章算术》“割圆术”中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这里所用的割圆术所体现的是一种由有限到无限的转化思想.比如在求的和中,“…”代表按此规律无限个数相加不断求和.我们可设 . 则有 , 即 , 解得 , 故 .
15. 在《九章算术》“割圆术”中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这里所用的割圆术所体现的是一种由有限到无限的转化思想.比如在求的和中,“…”代表按此规律无限个数相加不断求和.我们可设 . 则有 , 即 , 解得 , 故 .类似地,请你计算: . (直接填计算结果即可)
三、解答题
-
16. 计算:17. 解分式方程: .18. 如图,反比例函数的图象与一次函数的图象交于M(1,3),N两点,点N的横坐标为-3.
 (1)、根据图象信息可得关于x的方程的解为;(2)、求一次函数的解析式.19. 为了解市民对江门市创建全国文明城市工作的满意程度,某学校数学兴趣小组在骏景湾小区内进行了调查统计.将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,有意隐去了一些数据,得到不完整的统计图表,设计了一道数学题.
(1)、根据图象信息可得关于x的方程的解为;(2)、求一次函数的解析式.19. 为了解市民对江门市创建全国文明城市工作的满意程度,某学校数学兴趣小组在骏景湾小区内进行了调查统计.将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,有意隐去了一些数据,得到不完整的统计图表,设计了一道数学题.
请结合图中的信息,解决下列问题:
(1)、请求出接受问卷调查的人数,并补全条形统计图;(2)、请求出扇形统计图中“满意”部分的圆心角度数;(3)、该兴趣小组准备从调查结果为“不满意”的位市民中随机选择位进行回访,已知这位市民中有位男性,位女性.请用画树状图或列表的方法求出选择回访的市民为“一男一女”的概率.20. 某商城销售一新款耳机,每件进价为30元,经过试销发现,该耳机每天的销售量y(件)与销售单价x(元)之间满足如下关系: .(1)、求该商店销售这款耳机每天获得的利润w(元)与x之间的函数关系式;(2)、销售单价定为多少时,每天能获得最大的利润?每天利润的最大值是多少元?21. 如图,已知:梯形ABCD中,AD∥BC,E为AC的中点,连接DE并延长交BC于点F,连接AF.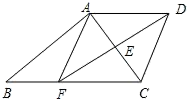 (1)、求证:AD=CF;(2)、在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.
(1)、求证:AD=CF;(2)、在原有条件不变的情况下,请你再添加一个条件(不再增添辅助线),使四边形AFCD成为菱形,并说明理由.

