广东省惠阳区2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 下列各数中,最大的数是( )A、2 B、 C、 D、2. 新冠病毒的直径大约是0.00000014米,呈圆形或者椭圆形,主要通过呼吸道进行传播.数据0.00000014用科学记数法表示( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下面几何体中,其主视图与俯视图相同的是( )
A、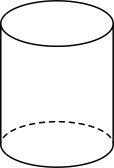
B、
B、
C、
C、
D、
D、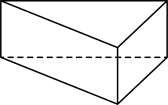
5. 如图, , 则的度数( )
5. 如图, , 则的度数( )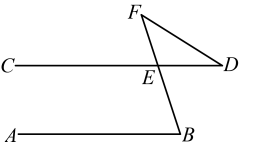 A、 B、 C、 D、6. 一次数学测试,甲、乙两班同学的成绩统计并分析如图所示,则下列说法正确的是( )
A、 B、 C、 D、6. 一次数学测试,甲、乙两班同学的成绩统计并分析如图所示,则下列说法正确的是( )参加人数
平均数
中位数
方差
甲
50
85
83
5.1
乙
50
85
85
4.6
A、甲班的成绩比乙班的成绩稳定 B、小明得84分将排在甲班的前25名 C、甲,乙两班竞赛成绩的众数相同 D、甲班的整体成绩比乙班好7. 二次根式有意义,则x的取值为( )A、 B、 C、 D、8. 如果一个多边形的内角和等于900°,这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形9. 若 , 则的值为( )A、8 B、7 C、5 D、610. 二次函数的图像如图所示,有下列结论:①;②;③;④ .
其中正确的有( )
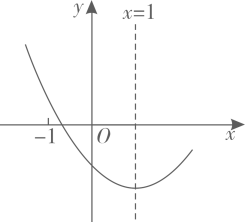 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 分解因式: .12. 如图,在平行四边形中,E是边上的中点,连接 , 并延长交延长线于点F,则与平行四边形的面积之比是 .
 13. 若 , 则的值为 .14. 为了测量校园水平地面上一棵不可攀爬的树的高度,小明利用物理学中“光的反射定律”做了如下的探索:如图,找一面很小的镜子放在合适的位置(点E处),小明站在点D处刚好能在镜子里看到树梢顶点,此时小明看镜子的视线与地面的夹角为(即),镜子到大树的水平距离为30米,则树的高度为米(注:反射角等于入射角,结果若有根号则保留根号).
13. 若 , 则的值为 .14. 为了测量校园水平地面上一棵不可攀爬的树的高度,小明利用物理学中“光的反射定律”做了如下的探索:如图,找一面很小的镜子放在合适的位置(点E处),小明站在点D处刚好能在镜子里看到树梢顶点,此时小明看镜子的视线与地面的夹角为(即),镜子到大树的水平距离为30米,则树的高度为米(注:反射角等于入射角,结果若有根号则保留根号). 15. 如图,在中, , , 分别以点为圆心,相同半径画弧,弧线分别相交有两个交点,连接这两个交点的直线交于点D,连接 , 则 . (结果若有根号则保留根号)
15. 如图,在中, , , 分别以点为圆心,相同半径画弧,弧线分别相交有两个交点,连接这两个交点的直线交于点D,连接 , 则 . (结果若有根号则保留根号)
三、解答题
-
16. 解不等式组 , 并求不等式组的正整数解.17. 先化简,再求值: , 其中 .18. 为帮助学生养成热爱美、发现美的艺术素养,某校开展了“一人一艺”的艺术选修课活动.学生根据自己的喜好选择一门艺术项目(A:书法,B:绘画,C:摄影,D:泥塑,E:剪纸),张老师随机对该校部分学生的选课情况进行调查后,制成了两幅不完整的统计图(如图所示).根据统计图信息完成下列问题:
 (1)、张老师调查的学生人数是 , 其中选择“D泥塑”选修课的人数是 , “E剪纸”项目在扇形统计图中圆心角的度数为;若该校共有学生1000名,请估计全校选修“B绘画”的学生人数约是 .(2)、现有4名学生,其中2人选修书法,1人选修绘画,1人选修摄影,张老师要从这4人中任选2人了解他们对艺术选修课的看法,请用画树状图或列表的方法(用ABC表示),求所选2人都是选修“书法”的概率.19. 疫情全面开放以来,旅游业迅速升温,某旅行社为吸引广大市民组团去H市旅游,推出了如下收费标准:如果人数不超过10人,人均旅游费用为350元,如果人数超过10人,每增加1人,人均旅游费用降低5元,但人均旅游费用不得低于280元.(1)、如果某公司组织12人参加去H市旅游,那么需人均支付旅行社旅游费用元;(2)、现某公司组织员工去H市旅游,共支付给该旅行社旅游费用6000元,那么该单位有多少名员工参加旅游?20. 如图,一次函数的图像与反比例函数的图像交于点 , 与x轴,y轴分别交于点 , 已知点A的纵坐标为1
(1)、张老师调查的学生人数是 , 其中选择“D泥塑”选修课的人数是 , “E剪纸”项目在扇形统计图中圆心角的度数为;若该校共有学生1000名,请估计全校选修“B绘画”的学生人数约是 .(2)、现有4名学生,其中2人选修书法,1人选修绘画,1人选修摄影,张老师要从这4人中任选2人了解他们对艺术选修课的看法,请用画树状图或列表的方法(用ABC表示),求所选2人都是选修“书法”的概率.19. 疫情全面开放以来,旅游业迅速升温,某旅行社为吸引广大市民组团去H市旅游,推出了如下收费标准:如果人数不超过10人,人均旅游费用为350元,如果人数超过10人,每增加1人,人均旅游费用降低5元,但人均旅游费用不得低于280元.(1)、如果某公司组织12人参加去H市旅游,那么需人均支付旅行社旅游费用元;(2)、现某公司组织员工去H市旅游,共支付给该旅行社旅游费用6000元,那么该单位有多少名员工参加旅游?20. 如图,一次函数的图像与反比例函数的图像交于点 , 与x轴,y轴分别交于点 , 已知点A的纵坐标为1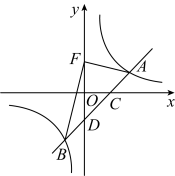 (1)、求一次函数的表达式;(2)、求B点的坐标,并直接写出时x的取值范围21. 如图,锐角 , 以为直径的与边交于点D,与边交于点F,过点D作 , 垂足为点E,连接 .
(1)、求一次函数的表达式;(2)、求B点的坐标,并直接写出时x的取值范围21. 如图,锐角 , 以为直径的与边交于点D,与边交于点F,过点D作 , 垂足为点E,连接 . (1)、求证:是的切线;(2)、若 , 求和弧围成的阴影部分的面积.22. 如图1,正方形的边长为5,点E为正方形边上一动点,过点B作于点P,将绕点A逆时针旋转得 , 连接 .
(1)、求证:是的切线;(2)、若 , 求和弧围成的阴影部分的面积.22. 如图1,正方形的边长为5,点E为正方形边上一动点,过点B作于点P,将绕点A逆时针旋转得 , 连接 . (1)、证明: .(2)、延长交于点F.判断四边形的的形状,并说明理由;(3)、若 , 求线段的长度23. 如图,已知抛物线与x轴的一个交点为 , 与y轴交于点A.
(1)、证明: .(2)、延长交于点F.判断四边形的的形状,并说明理由;(3)、若 , 求线段的长度23. 如图,已知抛物线与x轴的一个交点为 , 与y轴交于点A.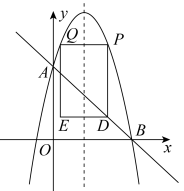 (1)、求抛物线的解析式;(2)、若点P是抛物线上位于直线上方的动点,分别过点P作x轴的平行线交抛物线于点Q,作y轴的平行线交直线于点D,以为边作矩形 , 求矩形周长的最大值,并求出此时点P的坐标;(3)、若点N是抛物线对称轴上的一点,在抛物线上是否存在一点M,使得以为顶点的四边形是平行四边形?不存在,则说明理由;若存在,请求出点M的坐标.
(1)、求抛物线的解析式;(2)、若点P是抛物线上位于直线上方的动点,分别过点P作x轴的平行线交抛物线于点Q,作y轴的平行线交直线于点D,以为边作矩形 , 求矩形周长的最大值,并求出此时点P的坐标;(3)、若点N是抛物线对称轴上的一点,在抛物线上是否存在一点M,使得以为顶点的四边形是平行四边形?不存在,则说明理由;若存在,请求出点M的坐标.