广东省广州市从化区2023年中考一模数学试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 在、、、四个数中,属于无理数的是( )A、 B、 C、 D、2. 下面四个立体图形中主视图是三角形的是( )A、
 B、
B、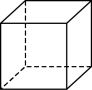 C、
C、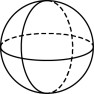 D、
D、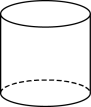 3. 代数式有意义的条件是( )A、 B、 C、且 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在平行四边形中,与交于O点,则下列结论中不一定成立的是( )
3. 代数式有意义的条件是( )A、 B、 C、且 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,在平行四边形中,与交于O点,则下列结论中不一定成立的是( )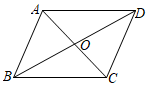 A、 B、 C、 D、6. 实数a、b在数轴上的位置如图所示,则下列结论不正确的是( )
A、 B、 C、 D、6. 实数a、b在数轴上的位置如图所示,则下列结论不正确的是( )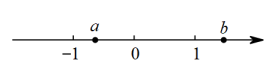 A、 B、 C、 D、7. 如图所示,电路连接完好,且各元件工作正常.随机闭合开关、、中的两个,能让两个小灯泡同时发光的概率是( )
A、 B、 C、 D、7. 如图所示,电路连接完好,且各元件工作正常.随机闭合开关、、中的两个,能让两个小灯泡同时发光的概率是( )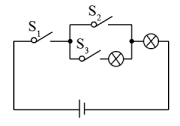 A、 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、9. 如图,在中, , , , 点F在上,并且 , 点E为上的动点(点E不与点C重合),将沿直线翻折,使点C落在点P处,的长为 , 则边的长为( )
A、 B、 C、 D、8. 若点 , , 都在反比例函数的图象上,则、、的大小关系是( )A、 B、 C、 D、9. 如图,在中, , , , 点F在上,并且 , 点E为上的动点(点E不与点C重合),将沿直线翻折,使点C落在点P处,的长为 , 则边的长为( )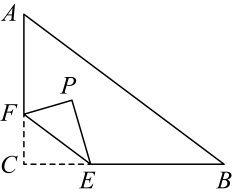 A、 B、3 C、 D、410. 二次函数()的图象如图所示,则下列结论中正确的有( )个
A、 B、3 C、 D、410. 二次函数()的图象如图所示,则下列结论中正确的有( )个①;②;③函数的最大值为;④当时,;⑤时,y随x增大而减少
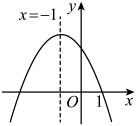 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
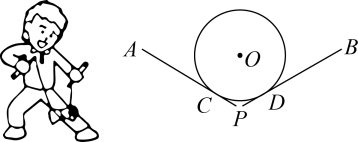
11. 嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,该速度112000用科学记数法表示为 .12. 因式分解: .13. 将点先向左平移1个单位长度,再向上平移2个单位长度得到点 , 则点的坐标为 .14. 一元二次方程有两个相等的实数根,则a= .15. 抖空竹是中国传统文化苑中一株灿烂的花朵,是国家级的非物质文化遗产之一,可见于全国各地,天津、北京、辽宁、吉林、黑龙江等地尤为盛行.如图,、分别与相切于点C、D,延长、交于点P.若 , 的直径为 , 则图中的长为 . (结果保留)
 16. 如图,、、、…、都是斜边在x轴上的等腰直角三角形,点、、、…、都在x轴上,点、、、…、都在反比例函数的图象上,则点的坐标为 , 点的坐标为 .
16. 如图,、、、…、都是斜边在x轴上的等腰直角三角形,点、、、…、都在x轴上,点、、、…、都在反比例函数的图象上,则点的坐标为 , 点的坐标为 .
三、解答题
-
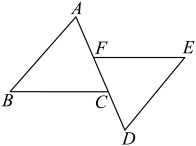
17. 解不等式组: .18. 如图,点F、C是上的两点,且 , , . 求证: .
 19. 已知 .(1)、化简T;(2)、若a、b为方程的两个根,求T的值.20. 果农小林家的荔枝喜获丰收.在销售过程中,荔枝的销售额y(元)与销量x(千克)满足(),下表是荔枝销售额与销量的数量关系.
19. 已知 .(1)、化简T;(2)、若a、b为方程的两个根,求T的值.20. 果农小林家的荔枝喜获丰收.在销售过程中,荔枝的销售额y(元)与销量x(千克)满足(),下表是荔枝销售额与销量的数量关系.销量x(千克)
1
2
3
…
销售额y(元)
8
14
20
…
(1)、求y与x的函数关系式;(2)、当荔枝销售额为1592元时,销量是多少千克?21. 随着中高考的改革,阅读的重要性也越来越凸显,阅读力成为学习力之一.某校开展了九年级学生一周阅读打卡活动,为了解一周阅读打卡活动的情况,随机抽查了该校九年级200名学生阅读打卡的天数,并根据抽查结果制作了如下不完整的频数分布直方图: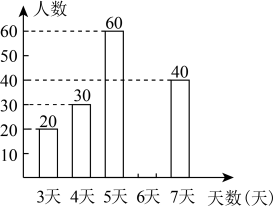
根据以上恴息,解答下列问题:
(1)、请补全频数分布直方图;(2)、被调查的200名学生阅读打卡天数的众数为 , 中位数为 , 平均数为;(3)、若该校有九年级学生1000人,请你估计该校九年级学生阅读打卡不少于5天的人数.22. 如图,在中, , 以为直径的与交于点D,连接 .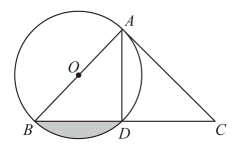 (1)、尺规作图:作出劣弧的中点E(不写作法,保留作图痕迹);(2)、连接交于F点,连接 , 求证:;(3)、若的半径等于6,且与相切于A点,求阴影部分的面积(结果保留).23. 为了测量流溪河某段河流的宽度,两个数学研究小组设计了不同的方案,他们在河西岸的点A处测得河东岸的树H恰好在A的正东方向.测量方案与数据如下表:
(1)、尺规作图:作出劣弧的中点E(不写作法,保留作图痕迹);(2)、连接交于F点,连接 , 求证:;(3)、若的半径等于6,且与相切于A点,求阴影部分的面积(结果保留).23. 为了测量流溪河某段河流的宽度,两个数学研究小组设计了不同的方案,他们在河西岸的点A处测得河东岸的树H恰好在A的正东方向.测量方案与数据如下表:课题
测量河流宽度
测量工具
测量角度的仪器,皮尺等
测量小组
第一小组
第二小组
测量方案示意图
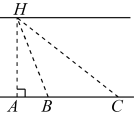
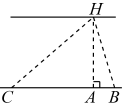
说明
点B,C在点A的正南方
点B在点A的正南方向,点C在点A的正北方向
测量数据
(1)、求的度数;(2)、请选择其中一个方案及其数据求出河宽(精确到);(参考数据: , , , )
