广东省番禺区2023年中考一模数学试题
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 如图,若点A,B,C所对应的数为a,b,c,则下列大小关系正确的是( )
 A、 B、b<-c<a C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 图中的图形为轴对称图形,该图形的对称轴的条数为( )
A、 B、b<-c<a C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 图中的图形为轴对称图形,该图形的对称轴的条数为( ) A、1 B、2 C、3 D、54. 要使分式 有意义,x的取值应满足( )A、 B、 C、 D、5. 不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )A、 B、 C、 D、6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、8. 如图,在边长为6的正方形中,以为直径画半圆,则阴影部分的面积是( )
A、1 B、2 C、3 D、54. 要使分式 有意义,x的取值应满足( )A、 B、 C、 D、5. 不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )A、 B、 C、 D、6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 若关于的一元二次方程有两个相等的实数根,则实数的值为( )A、 B、 C、 D、8. 如图,在边长为6的正方形中,以为直径画半圆,则阴影部分的面积是( ) A、9 B、6 C、 D、9. 如图,在中, , 将绕点C逆时针旋转得到 , 点A,B的对应点分别为D,E,连接 . 当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A、9 B、6 C、 D、9. 如图,在中, , 将绕点C逆时针旋转得到 , 点A,B的对应点分别为D,E,连接 . 当点A,D,E在同一条直线上时,下列结论一定正确的是( ) A、 B、 C、 D、10. 如图,菱形中,.动点P从点B出发,以每秒1个单位长度的速度沿折线运动到点C,同时动点Q从点A出发,以相同速度沿折线运动到点D,当一个点停止运动时,另一点也随之停止.设的面积为y,运动时间为x秒.则下列图象能大致反映y与x之间函数关系的是( )
A、 B、 C、 D、10. 如图,菱形中,.动点P从点B出发,以每秒1个单位长度的速度沿折线运动到点C,同时动点Q从点A出发,以相同速度沿折线运动到点D,当一个点停止运动时,另一点也随之停止.设的面积为y,运动时间为x秒.则下列图象能大致反映y与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 若在实数范围内有意义,则实数x的取值范围是 .12. 分解因式: .13. 随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7(毫米2),这个数用科学记数法表示为 .14. 在甲、乙两位射击运动员的10次考核成绩中,两人的考核成绩的平均数相同, 方差分别为 , , 则考核成绩更为稳定的运动员是(填“甲”、“乙”中的一个)15. 把光盘、含60°角的三角板和直尺如图摆放,光盘与直尺和三角板的一边相切,若 , 则光盘的直径是 .
 16. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
16. 在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 称为点A的“倒数点”.如图,矩形 的顶点C为 ,顶点E在y轴上,函数 的图象与 交于点A.若点B是点A的“倒数点”,且点B在矩形 的一边上,则 的面积为.
三、解答题
-
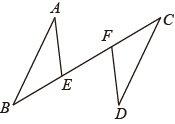
17. 解不等式组 , 并将解集在数轴上表示出来.18. 如图,点E、F在线段BC上, , , ,证明: .
 19. 已知(1)、化简T。(2)、若正方形ABCD的边长为a,且它的面积为9,求T的值。20. 为了进一步改善人居环境,提高居民生活的幸福指数.某小区物业公司决定对小区环境进行优化改造.如图,AB表示该小区一段长为的斜坡,坡角于点D.为方便通行,在不改变斜坡高度的情况下,把坡角降为.
19. 已知(1)、化简T。(2)、若正方形ABCD的边长为a,且它的面积为9,求T的值。20. 为了进一步改善人居环境,提高居民生活的幸福指数.某小区物业公司决定对小区环境进行优化改造.如图,AB表示该小区一段长为的斜坡,坡角于点D.为方便通行,在不改变斜坡高度的情况下,把坡角降为.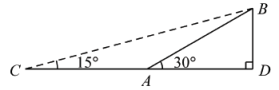 (1)、求该斜坡的高度BD;(2)、求斜坡新起点C与原起点A之间的距离.(假设图中C,A,D三点共线)21. 我区某中学举行书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下图所示的两幅不完整的统计图,请结合图中相关数据解答下列问题;
(1)、求该斜坡的高度BD;(2)、求斜坡新起点C与原起点A之间的距离.(假设图中C,A,D三点共线)21. 我区某中学举行书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下图所示的两幅不完整的统计图,请结合图中相关数据解答下列问题; (1)、请补全条形统计图;(2)、获得一等奖的同学中有来自七年级,有来自八年级,其他同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率.22. 如图,平面直角坐标系 中, 的边 在 轴上,对角线 , 交于点 ,函数 的图象经过点 和点 .
(1)、请补全条形统计图;(2)、获得一等奖的同学中有来自七年级,有来自八年级,其他同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请通过列表或画树状图求所选出的两人中既有七年级又有九年级同学的概率.22. 如图,平面直角坐标系 中, 的边 在 轴上,对角线 , 交于点 ,函数 的图象经过点 和点 .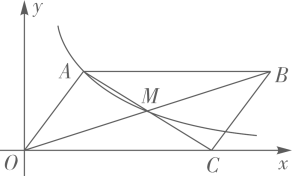 (1)、求 的值和点 的坐标;(2)、求 的周长.23. 如图,是的直径,点C在上,且 .
(1)、求 的值和点 的坐标;(2)、求 的周长.23. 如图,是的直径,点C在上,且 . (1)、尺规作图:过点O作的垂线,交劣弧于点D,连接(保留作图痕迹,不写作法);(2)、在(1)所作的图形中,求点O到的距离及的值.
(1)、尺规作图:过点O作的垂线,交劣弧于点D,连接(保留作图痕迹,不写作法);(2)、在(1)所作的图形中,求点O到的距离及的值.
