广东省大亚湾区2023年中考一模数学试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 在中,是无理数的是( )A、 B、 C、 D、22. 科学家在实验室中检测出某种病毒的直径约为0.000000103米,该直径用科学记数法表示为( )A、米 B、米 C、米 D、米3. 下列计算正确的是( )A、 B、 C、 D、4. 不等式组的解集是( )A、 B、 C、 D、5. 如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
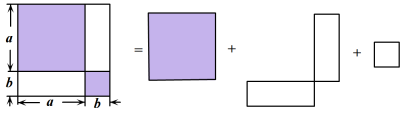 A、 B、 C、 D、6. 某班一合作学习小组有5人,某次数学测试成绩数据分别为65、78、86、91、85,则这组数据的中位数是( )A、78 B、85 C、86 D、917. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( )
A、 B、 C、 D、6. 某班一合作学习小组有5人,某次数学测试成绩数据分别为65、78、86、91、85,则这组数据的中位数是( )A、78 B、85 C、86 D、917. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( ) A、40° B、60° C、80° D、100°8. 如图,在中, , D,E,F分别为 , , 的中点.若EF的长为10,则的长为( )
A、40° B、60° C、80° D、100°8. 如图,在中, , D,E,F分别为 , , 的中点.若EF的长为10,则的长为( ) A、5 B、10 C、15 D、209. 某物流公司有两种货车,已知每辆大货车的货运量比每辆小货车的货运量多4吨,且用大货车运送80吨货物所需车辆数与小货车运送60吨货物所需车辆数相同.每辆大、小货车货运量分别是多少吨?设每辆小货车的货运量是x吨,则列方程正确的是( )A、 B、 C、 D、10. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论:
A、5 B、10 C、15 D、209. 某物流公司有两种货车,已知每辆大货车的货运量比每辆小货车的货运量多4吨,且用大货车运送80吨货物所需车辆数与小货车运送60吨货物所需车辆数相同.每辆大、小货车货运量分别是多少吨?设每辆小货车的货运量是x吨,则列方程正确的是( )A、 B、 C、 D、10. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: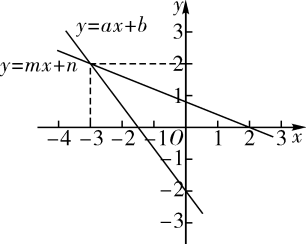
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 八边形的外角和为 .12. 分解因式: .13. 若分式 的值为2,则x的值是.14. 如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为 .
 15. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走60米至观测点D,测得A在D的正北方向,B在D的北偏西方向上,A,B两点间的距离为米.
15. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走60米至观测点D,测得A在D的正北方向,B在D的北偏西方向上,A,B两点间的距离为米.
三、解答题
-
16. 计算:.17. 如图,在中, , , 平分交于点D.
 (1)、尺规作图:在中,作边上的高(保留痕迹,不写作法);(2)、在(1)的条件下,求的度数.18. 已知:点是反比例函数的图象与直线的一个交点.
(1)、尺规作图:在中,作边上的高(保留痕迹,不写作法);(2)、在(1)的条件下,求的度数.18. 已知:点是反比例函数的图象与直线的一个交点. (1)、求k、m的值;(2)、当时,请直接写出x的取值范围.19. 若关于x的一元二次方程有两个实数根(1)、试确定实数m的取值范围;(2)、若 , 求m的值.20. 如图,在四边形ABCD中,ABCD,AC平分∠DAB,AB=2CD,E为AB中点,连接CE.
(1)、求k、m的值;(2)、当时,请直接写出x的取值范围.19. 若关于x的一元二次方程有两个实数根(1)、试确定实数m的取值范围;(2)、若 , 求m的值.20. 如图,在四边形ABCD中,ABCD,AC平分∠DAB,AB=2CD,E为AB中点,连接CE.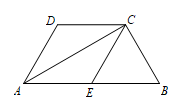 (1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积.21. 为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,发现每户用水量在吨之间,结果如图所示.
(1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积.21. 为了倡导保护资源节约用水,从某小区随机抽取了50户家庭,调查了他们5月的用水量情况,发现每户用水量在吨之间,结果如图所示. (1)、这50户家庭中5月用水量在的有多少户?(2)、把图中每组用水量的值用该组的中间值(如的中间值为5)来代替,估计该小区平均每户用水量;(3)、从该50户用水量在的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在的概率.
(1)、这50户家庭中5月用水量在的有多少户?(2)、把图中每组用水量的值用该组的中间值(如的中间值为5)来代替,估计该小区平均每户用水量;(3)、从该50户用水量在的家庭中,任抽取2户,用树状图或表格法求至少有1户用水量在的概率.

