安徽省舒城县2023年中考模拟数学试题

试卷更新日期：2023-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{5}$ 的倒数是（）

A、5 B、 $- 5$ C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 《2023年国务院政府工作报告》指出，去年我国经济保持恢复发展，国内生产总值增长 $8.1 %$ ，城镇新增就业 $1269$ 万人， $1269$ 万用科学记数法表示为（）

A、 $1.269 \times 1 0^{7}$ B、 $1.269 \times 1 0^{8}$ C、 $1269 \times 1 0^{4}$ D、 $0.1269 \times 1 0^{8}$

查看试题解析
3. 如图所示的杯子，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 ${(- 2 a^{3})}^{2} = 4 a^{6}$ B、 $7 a^{2} \cdot a^{3} = 7 a^{6}$ C、 $a^{3} + 3 a^{3} = 4 a^{6}$ D、 $a^{8} \div a^{2} = a^{4}$

查看试题解析
5. 在压力不变的情况下，某物体承受的压强（单位： $P a$ ）与它的受力面积（单位： $m^{2}$ ）是反比例函数关系，平平记录了几次测量所得的数据，由于疏忽，其中有一次记录的数据有误，观察表格，有误的那一次是（）

第1次
第2次
第3次
第4次
…
受力面积 $(m^{2})$
0.1
0.2
0.3
0.4
…
压强 $(P a)$
1000
500
300
250
…

A、第1次 B、第2次 C、第3次 D、第4次

查看试题解析
6. 下列从左到右是因式分解且正确的是（）

A、 $x^{2} - 4 = {(x - 2)}^{2}$ B、 ${(x + 1)}^{2} = x^{2} + 2 x + 1$ C、 $x^{2} - 4 - 4 x = (x - 2) (x + 2) - 4 x$ D、 $x y + x = x (y + 1)$

查看试题解析
7. 2022年世界杯足球赛在卡塔尔举行，阿根廷、克罗地亚、法国和摩洛哥四支球队进入四强．海川中学足球社团在“你最喜爱的球队”调查中，随机调查了全社团成员（每名成员从中分别选一个球队），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢法国队的人数比最喜欢阿根廷队的人数少6人，则该社团成员总人数是（）

A、100 B、40 C、80 D、60

查看试题解析
8. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，点P在 $\overset{⌢}{A F}$ 上，Q是 $\overset{⌢}{D E}$ 的中点，则 $∠ C P Q$ 的度数为（）

A、 $30 °$ B、 $36 °$ C、 $45 °$ D、 $60 °$

查看试题解析
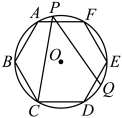9. 将一张 $▱ A B C D$ （ $A D < A B < 2 A D$ ）纸片，以它的一边为边长剪去一个菱形，将余下的平行四边形中，再以它的一边为边长剪去一个菱形，若剪去两个菱形后所剩下的平行四边形与原来 $▱ A B C D$ 相似，则 $▱ A B C D$ 的相邻两边 $A D$ 与 $A B$ 的比值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{2}}{2}$ 或 $\frac{\sqrt{5} - 1}{2}$ D、 $\sqrt{2} - 1$ 或 $\frac{\sqrt{2}}{2}$ 或 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
10. 如图，在平面直角坐标系中，点A，B的坐标分别为 $A (0 ， 3)$ ， $B (4 ， 0)$ ，点P为坐标平面内任意满足 $A P = 1$ 的点，点Q为线段 $B P$ 的中点，连接 $O Q$ ，则 $O Q$ 的最大值为（）

A、 $\frac{7}{2}$ B、3 C、 $\frac{5}{2}$ D、2

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} x - 1 ≥ 0 \\ 4 - 2 x < 0 \end{array}$ 的解集是.

查看试题解析
12. 如图，直线 $a ∥ b$ ，直线 $A B$ 交a，b于点A，B， $∠ B A D$ 的平分线交直线b于点C，若 $∠ 1 = 55 °$ ，则 $∠ 2$ 的度数是．

查看试题解析
13. 如图，在 $△ A B C$ 中，点D在边 $A B$ 上，点E在边 $B C$ 上，把 $△ D B E$ 沿直线 $D E$ 折叠， $△ D B E$ 恰好与 $△ D C E$ 重合， $C D = A C$ ．若 $B C = 6$ ， $△ B C D$ 的面积为3，则 $A D$ 的长为．

查看试题解析
14. 已知直线 $y_{1} = k x - 4 k$ 经过抛物线 $y_{2} = a x^{2} - 4 a x (a \neq 0)$ 的顶点，且当 $x < 2$ 时， $y_{1} > y_{2}$ ．则：

(1)、直线 $y_{1}$ 与抛物线 $y_{2}$ 都经过同一个定点，这个定点的坐标是．

(2)、当 $y_{2} > y_{1}$ 时，x的取值范围是．

查看试题解析

三、解答题

15. 计算： $| - 1 | - \frac{1}{2} \sqrt{12} + {(5 - π)}^{0} + 2 c o s 30 °$ ．

查看试题解析
16. 如图，在边长为1的正方形的网格中，已知 $△ A B C$ 及直线l．
（ 1 ）将 $△ A B C$ 向右平移1个单位，再向下平移2个单位，得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ；
（ 2 ）画出 $△ A_{1} B_{1} C_{1}$ 关于直线l的对称图形 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
17. 创新科技公司生产A，B，两种 $A I$ 新产品，A种产品敏天产量是B种产品的每天产量 $150 %$ ，两种产品各生产 $6000$ 件，A种产品生产所需天数比B种产品少用1天．求该公司每天生产A，B两种产品多少件？

查看试题解析
18. 观察下列等式：
第1个等式： $1^{3} + 1 - 0^{2} \times 2 = 1 \times 2$ ；
第2个等式： $2^{3} + 1 - 1^{2} \times 3 = 2 \times 3$ ；
第3个等式： $3^{3} + 1 - 2^{2} \times 4 = 3 \times 4$ ；
第4个等式： $4^{3} + 1 - 3^{2} \times 5 = 4 \times 5$ ；
……

(1)、根据等式中的规律，写出第6个等式：；

(2)、猜想并写出第n个等式，并证明它的正确性．

查看试题解析
19. 中国人民海军南海舰队在南海巡航，一艘驱逐舰位于某岛礁P（如图所示）的北偏东 $60 °$ 方向，且与P点的距离为 $20$ 海里的A处，发现一艘外舰擅自进入中国南海有关岛礁邻近海域，我驱逐舰迅即行动，沿正南方向以每小时30海里的速度快速航行，并于岛礁P的南偏东 $45 °$ 方向上的B处追上外舰，依法依规对外舰进行识别查证，并予以警告驱离．（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{6} \approx 2.45$ ）

(1)、求B点与我岛礁P之间的距离PB；（精确到0.1海里）

(2)、问我驱逐舰航行多长时间后到达B处？（精确到0.1小时）

查看试题解析
20. 如图， $A B$ 是半 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的切线，C为切点， $O D ⊥ A B$ 于O， $O D$ 与 $A C$ 交于点E．

(1)、求证： $∠ D E C = ∠ D C E$ ；

(2)、连接 $A D$ 与半 $⊙ O$ 相交于点F，若 $⊙ O$ 的半径为3， $O E = 1$ ，求点O到 $A D$ 的距离．

查看试题解析
21. 某县为进一步落实新课程标准理念，组织全县 $6000$ 名教师参加新课程标准知识测试，测试后发现所有教师的成绩均不低于 $50$ 分．为了更好地了解本次测试的成绩分布情况，随机抽取了其中 $200$ 名教师的成绩（成绩x取整数，总分 $100$ 分）作为样本进行整理，得到下列不完整的统计图表，部分信息如下：
组名
成绩/分
频数
A
$50 \leq x < 60$
$10$
B
$60 \leq x < 70$
$20$
C
$70 \leq x < 80$
$30$
D
$80 \leq x < 90$
E
$90 \leq x \leq 100$
80

(1)、这次测试成绩的中位数会落在哪一组？请补全频数分布直方图；

(2)、若成绩在 $90$ 分以上（包括 $90$ 分）的为“优”等，则该县参加这次测试的 $6000$ 名教师中成绩为“优”等的大约有多少人？

(3)、已知这次测试有5名教师（3女2男）获得满分，现从中任选两人参加所在市组织的“全面育人、素养导向”大赛，求恰巧选中一名男教师和一名女教师的概率．

查看试题解析
22. 如图，等腰 $R t △ A B C$ ， $∠ A C B = 90 °$ ，分别以 $A B$ ， $A C$ 为边长在 $A B$ 同侧作等边 $△ A B D$ 和等边 $△ A C E$ ， $A D$ 与 $C E$ 相交于点F，连接 $D E$ ， $D C$ ．

(1)、求证： $B C = D E$ ；

(2)、求证： $C D^{2} = A C \cdot F C$ ；

(3)、已知 $A B = 2$ ，求线段 $E F$ 的长．

查看试题解析
23. 如图，直线 $y = x - 3$ 与抛物线 $y = - x^{2} + b x + c$ 相交于A，B两点，与抛物线对称轴交于点M，且点A，B分别在x轴，y轴上，抛物线的顶点为C．

(1)、求抛物线的解析式和点M的坐标；

(2)、点N是线段 $C M$ 上的动点， $N P ⊥ C M$ 交B，C两点之间的抛物线于点P，点P的坐标为 $P (x ， n)$ ， $m = M P^{2}$ ．
①求 $N P^{2}$ （用含n的代数式表示）；
②求m与n之间的函数关系式，并求出m的最小值．

查看试题解析

	第1次	第2次	第3次	第4次	…
受力面积 $(m^{2})$	0.1	0.2	0.3	0.4	…
压强 $(P a)$	1000	500	300	250	…

组名	成绩/分	频数
A	$50 \leq x < 60$	$10$
B	$60 \leq x < 70$	$20$
C	$70 \leq x < 80$	$30$
D	$80 \leq x < 90$
E	$90 \leq x \leq 100$	80