安徽省怀远县2023年中考数学二模试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 如果 , 则a等于( )A、 B、 C、 D、以上都不对3. 2017年10月18 日上午9时,中国共产党第十九次全国代表大会在北京人民大会堂开幕.据统计,在 10月18日9时至10月19日9时期间,新浪微博话题#十九大#阅读量25.3亿,把数据 25.3 亿写成科学记数法正确的是( )A、25.3×108 B、2.53×108 C、2.53×109 D、25.3×1094. 如果m是 的整数部分,则m的值为( )A、1 B、2 C、3 D、45. 下列因式分解正确的是( )A、 B、 C、 D、6. 解方程 , 去分母正确的是( )A、 B、 C、 D、7. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、8. 春意复苏,郑州绿化工程正在如火如荼地进行着,某工程队计划将一块长64m,宽40m的矩形场地建设成绿化广场如图,广场内部修建三条宽相等的小路,其余区域进行绿化.若使绿化区域的面积为广场总面积的80%,求小路的宽,设小路的宽为x m,则可列方程( )
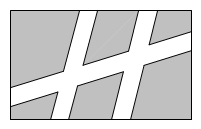 A、 B、 C、 D、9. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:(1);(2);(3);(4)若点、点、点在该函数图象上,则 . 其中正确的结论有( )
A、 B、 C、 D、9. 二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:(1);(2);(3);(4)若点、点、点在该函数图象上,则 . 其中正确的结论有( )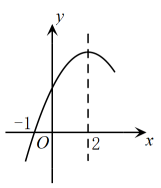 A、1个 B、2个 C、3个 D、4个10. 如图,、是的两条互相垂直的直径,点P从点O出发,沿的路线匀速运动.设(单位为度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
A、1个 B、2个 C、3个 D、4个10. 如图,、是的两条互相垂直的直径,点P从点O出发,沿的路线匀速运动.设(单位为度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )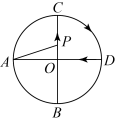 A、
A、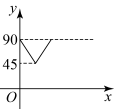 B、
B、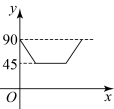 C、
C、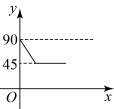 D、
D、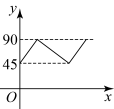
二、填空题
-
11. 当x时,在实数范围内有意义.12. 在国家政策的宏观调控下,某市的商品房成交均价由前年的元下降到今年的元 , 则这两年平均每年降价的百分率是 .13. 若反比例函数y= ,当x a或x a时,函数值y范围内的整数有k个;当x a+1或x -a-1时,函数值y范围内的整数有k-2个,则正整数a=.14. 抛物线的顶点坐标是 .
三、解答题
-
15. 计算: .16.(1)、计算;(2)、解方程: .17. 计算:18. 某公司为迎接哈洽会请甲乙两个广告公司布置展厅,若两公司合作天就可以完成任务,若甲公司先做天,剩余部分再由两公司合做,还需天才能完成任务.(1)、甲公司与乙公司单独完成这项任务各需多少天?(2)、甲公司每天所有费用为万元,乙公司每天所有费用为万元,要使这项工作的总费用不超过万元,则甲公司至多工作多少天?19. 现需运送一批货物,有甲、乙两种型号货车可供选择.两种型号货车出租价格如表:
起步价/元
限定里程/km
超限定里程(元/km)
甲
108
80
3
乙
180
100
2
租用甲种型号货车在限定里程80km内,只需付起步价108元,超过限定里程的部分按3元/km收费,租用乙种型号货车在限定里程100km内,只需支付起步价180元,超过限定里程的部分按2元/km收费,设里程为x千米.
(1)、当x>100时,用x分别表示租用甲、乙两种型号货车的费用;(2)、当里程为多少千米时,租用两种型号的货车费用相等?20. 某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的50%.在销售过程中发现:当销售单价为35元时,每天可售出350件,若销售单价每提高5元,则每天销售量减少50件.设销售单价为x元(销售单价不低于35元)(1)、求这种儿童玩具每天获得的利润w(元)与销售单价x(元)之间的函数表达式;(2)、当销售单价为多少元时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少元?21. 在平面直角坐标系中,点 , ,(1)、若a,b满足 , 求点A,B的坐标;(2)、如图 , 点C在直线上,且点C的坐标为 , 求m,n应满足怎样的关系式? (3)、如图 , 将线段平移到 , 且点D在直线上,且D点的纵坐标为x,当满足时,求x的取值范围.
(3)、如图 , 将线段平移到 , 且点D在直线上,且D点的纵坐标为x,当满足时,求x的取值范围. 22. 如图,在平面直角坐标系中,点在抛物线上,点也在此抛物线上,点C的坐标为 , 直线l过点 , 平行于x轴.设在直线l上方部分图形的面积为S.
22. 如图,在平面直角坐标系中,点在抛物线上,点也在此抛物线上,点C的坐标为 , 直线l过点 , 平行于x轴.设在直线l上方部分图形的面积为S.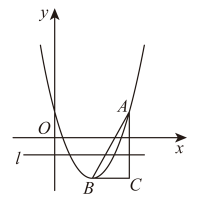 (1)、当时, , 当时, .(2)、根据(1)的结果,猜想当时,的值,并加以证明.(3)、求S与k的函数关系式.23. 已知二次函数的图象过点 , ,
(1)、当时, , 当时, .(2)、根据(1)的结果,猜想当时,的值,并加以证明.(3)、求S与k的函数关系式.23. 已知二次函数的图象过点 , , (1)、求此二次函数的解析式并在坐标系内画出其草图;(2)、求直线的解析式;(3)、点M是在第二象限内的该抛物线上,并且三角形的面积为 , 求点M的坐标.(4)、若点P在线段上以每秒一个单位长度的速度从点B向点A运动不与点A,B重合,点P停止运动时点Q随之而停止运动 , 同时,点Q在射线上以每秒个单位的速度从点A向点C运动,设运动时间为t秒,请求出三角形的面积S与t的函数关系式,并求出t为何值时,三角形的面积最大,最大值是多少?
(1)、求此二次函数的解析式并在坐标系内画出其草图;(2)、求直线的解析式;(3)、点M是在第二象限内的该抛物线上,并且三角形的面积为 , 求点M的坐标.(4)、若点P在线段上以每秒一个单位长度的速度从点B向点A运动不与点A,B重合,点P停止运动时点Q随之而停止运动 , 同时,点Q在射线上以每秒个单位的速度从点A向点C运动,设运动时间为t秒,请求出三角形的面积S与t的函数关系式,并求出t为何值时,三角形的面积最大,最大值是多少?