安徽省合肥市长丰县2023年中考二模数学试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、3 D、2. 如图,该几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
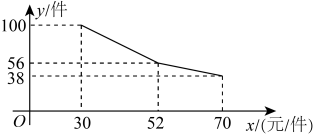
D、 3. 记者近日从市地方海事(港航)管理服务中心获悉,今年2月,合肥港港口货物吞吐量为万吨,港口集装箱吞吐量为万标箱,其中出港万标箱,同比增长 . 其中数据万用科学记数法表示为( )A、 B、 C、 D、4. 下列各式从左到右的变形正确的是( )A、 B、 C、 D、5. 某种水果的购买金额y(元)与购买量x(千克)之间的函数图象如图所示,当购买该种水果9千克时,需要付款( )
3. 记者近日从市地方海事(港航)管理服务中心获悉,今年2月,合肥港港口货物吞吐量为万吨,港口集装箱吞吐量为万标箱,其中出港万标箱,同比增长 . 其中数据万用科学记数法表示为( )A、 B、 C、 D、4. 下列各式从左到右的变形正确的是( )A、 B、 C、 D、5. 某种水果的购买金额y(元)与购买量x(千克)之间的函数图象如图所示,当购买该种水果9千克时,需要付款( )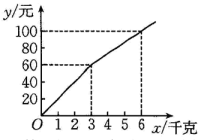 A、120元 B、140元 C、170元 D、180元6. 如图,直线 , 直线c交直线a于点A,交直线b于点B,直线c,若 , 则的度数为( )
A、120元 B、140元 C、170元 D、180元6. 如图,直线 , 直线c交直线a于点A,交直线b于点B,直线c,若 , 则的度数为( ) A、100° B、120° C、130° D、160°7. 随着网络直播平台的快速发展,直播砍价已让很多人趋之若鹜,某商品原售价为120元,在某直播平台上经过主播的两次砍价后,现售价为43.2元,已知每次砍价的百分率相同.设每次砍价的百分率为x,则下列方程正确的是( )A、 B、 C、 D、8. 白老师在黑板上计算一组数据时,列式如下: , 由公式提供的信息,下列关于这组数据的说法错误的是( )A、中位数是4 B、众数是4 C、平均数是4 D、方差是9. 如图,在中, , , , D是的中点,则的长为( ).
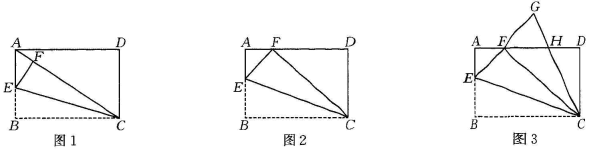
A、100° B、120° C、130° D、160°7. 随着网络直播平台的快速发展,直播砍价已让很多人趋之若鹜,某商品原售价为120元,在某直播平台上经过主播的两次砍价后,现售价为43.2元,已知每次砍价的百分率相同.设每次砍价的百分率为x,则下列方程正确的是( )A、 B、 C、 D、8. 白老师在黑板上计算一组数据时,列式如下: , 由公式提供的信息,下列关于这组数据的说法错误的是( )A、中位数是4 B、众数是4 C、平均数是4 D、方差是9. 如图,在中, , , , D是的中点,则的长为( ). A、 B、 C、3 D、410. 如图,是等边三角形,是等腰直角三角形, , 于点E,连接分别交 , 于点F,G,过点A作分别交 , 于点P,H,则下列结论不正确的是( )
A、 B、 C、3 D、410. 如图,是等边三角形,是等腰直角三角形, , 于点E,连接分别交 , 于点F,G,过点A作分别交 , 于点P,H,则下列结论不正确的是( )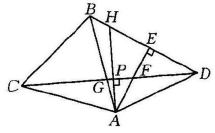 A、 B、 C、 D、若 , 则
A、 B、 C、 D、若 , 则二、填空题
-
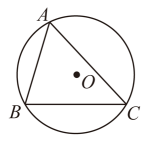
11. .12. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,即三角形的三边长分别为a,b,c,记 , 那么其面积 . 如果某个三角形的三边长分别为2,3,3,其面积S介于整数和n之间,那么n的值是 .13. 如图,内接于圆O.若 , , , 则的弧长为 .
 14. 如图,在矩形中, , , M,N分别是 , 上的动点,连接 , 交于点E,且 .
14. 如图,在矩形中, , , M,N分别是 , 上的动点,连接 , 交于点E,且 .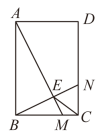 (1)、 .(2)、连接 , 则的最小值为 .
(1)、 .(2)、连接 , 则的最小值为 .三、解答题
-
15. 解不等式组: .16. 在平面直角坐标系中的位置如图所示,网格中小正方形的边长为1个单位长度.
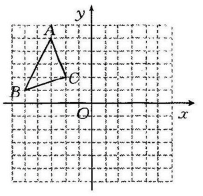 (1)、将沿x轴方向向右平移7个单位长度,再向下平移6个单位长度后得到 , 请画出 .(2)、将关于x轴对称得到 , 请画出 .17. 安徽浮山是中国第一文山,爬山是居民周末娱乐休闲、锻炼身体的方式之一.如图,某个周末小明同学从浮山山底沿斜坡爬了260米到达B处,紧接着又向上爬了坡角为的山坡90米,最后到达山顶处,若的坡度为 , 请你计算浮山的高度(结果精确到米,参考数据:).
(1)、将沿x轴方向向右平移7个单位长度,再向下平移6个单位长度后得到 , 请画出 .(2)、将关于x轴对称得到 , 请画出 .17. 安徽浮山是中国第一文山,爬山是居民周末娱乐休闲、锻炼身体的方式之一.如图,某个周末小明同学从浮山山底沿斜坡爬了260米到达B处,紧接着又向上爬了坡角为的山坡90米,最后到达山顶处,若的坡度为 , 请你计算浮山的高度(结果精确到米,参考数据:).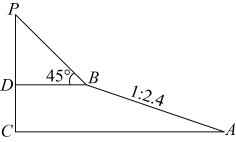 18. [观察思考]用同样大小的圆形棋子按如图所示的规律摆放:第1个图形中有6个棋子,第2个图形中有9个棋子,第3个图形中有12个棋子,第4个图形中有15个棋子,以此类推.
18. [观察思考]用同样大小的圆形棋子按如图所示的规律摆放:第1个图形中有6个棋子,第2个图形中有9个棋子,第3个图形中有12个棋子,第4个图形中有15个棋子,以此类推. (1)、[规律总结]
(1)、[规律总结]
第5个图形中有个圆形棋子.(2)、第n个图形中有个圆形棋子.(用含n的代数式表示)(3)、[问题解决]
现有2025个圆形棋子,若将这些棋子按照题中的规律一次性摆放,且棋子全部用完,则可摆放出第几个图形,请说明理由.19. 已知一次函数与反比例函数的图象都经过点 .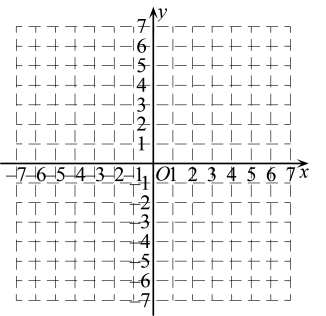 (1)、求a,b的值(2)、在图中画出一次函数与反比例函数的图象,并根据图象直接写出当一次函数值小于反比例函数值时,x的取值范围.20. 如图,点A,B,C在圆O上, , 直线 , , 点O在上.
(1)、求a,b的值(2)、在图中画出一次函数与反比例函数的图象,并根据图象直接写出当一次函数值小于反比例函数值时,x的取值范围.20. 如图,点A,B,C在圆O上, , 直线 , , 点O在上. (1)、求证是圆O的切线(2)、若 , 求圆O的半径.21. 随着中考的时间越来越近,学生的压力也越来越大.某校为了解本校九年级学生的压力情况,设计了一份调查问卷,对该校所有九年级的学生进行调查,并随机抽取部分调查结果,通过分析可将本校九年级学生的压力情况归纳为A(非常大),B(比较大),C(正常),D(没有压力)四种类型.具体分析数据如下统计图:
(1)、求证是圆O的切线(2)、若 , 求圆O的半径.21. 随着中考的时间越来越近,学生的压力也越来越大.某校为了解本校九年级学生的压力情况,设计了一份调查问卷,对该校所有九年级的学生进行调查,并随机抽取部分调查结果,通过分析可将本校九年级学生的压力情况归纳为A(非常大),B(比较大),C(正常),D(没有压力)四种类型.具体分析数据如下统计图: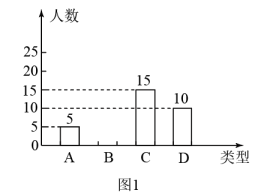
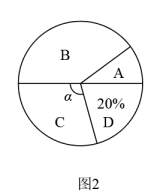 (1)、本次抽查的学生总人数为 , 在扇形统计图中,°.(2)、请把条形统计图补充完整.(3)、若感觉压力非常大的同学中有两名女同学,三名男同学,从中随机抽取两名同学进行心理疏导,求抽到的两名同学恰好是一男一女的概率.
(1)、本次抽查的学生总人数为 , 在扇形统计图中,°.(2)、请把条形统计图补充完整.(3)、若感觉压力非常大的同学中有两名女同学,三名男同学,从中随机抽取两名同学进行心理疏导,求抽到的两名同学恰好是一男一女的概率.