安徽省合肥市新站区2023年中考二模数学试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. 下列各式运算结果是负数的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 2023年春节假日期间,合肥市共接待游客万人,全市旅游综合收入亿元,其中数据万用科学记数法可表示为( )A、 B、 C、 D、4. 如图是一个正方体截去一角后得到的几何体,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 一个不等式的解集如图所示,则这个不等式可以是( )
5. 一个不等式的解集如图所示,则这个不等式可以是( )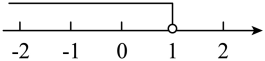 A、 B、 C、 D、6. 如图,直线 , 在等腰中, , , 顶点B在直线n上,直线m交于点E,交于点F,若 , 则的度数是( )
A、 B、 C、 D、6. 如图,直线 , 在等腰中, , , 顶点B在直线n上,直线m交于点E,交于点F,若 , 则的度数是( ) A、 B、 C、 D、7. 同一元素中质子数相同,中子数不同的各种原子互为同位素,如与、与 . 在一次制取的实验中,与的原子个数比为 , 与的原子个数比为 , 若实验恰好完全反应生成 , 则反应生成的概率( )A、 B、 C、 D、8. 如图,在菱形中,点E在的延长线上, , , , 求的长( )
A、 B、 C、 D、7. 同一元素中质子数相同,中子数不同的各种原子互为同位素,如与、与 . 在一次制取的实验中,与的原子个数比为 , 与的原子个数比为 , 若实验恰好完全反应生成 , 则反应生成的概率( )A、 B、 C、 D、8. 如图,在菱形中,点E在的延长线上, , , , 求的长( )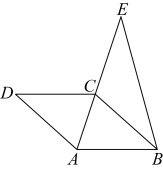 A、5 B、6 C、 D、9. 甲、乙两车从A城出发前往B城,其中甲先出发 , 如图是甲、乙行驶路程(km),(km)与时间x(h)变化的图像,下列说法不正确的是( )
A、5 B、6 C、 D、9. 甲、乙两车从A城出发前往B城,其中甲先出发 , 如图是甲、乙行驶路程(km),(km)与时间x(h)变化的图像,下列说法不正确的是( ) A、乙车开始行驶时,甲车在乙车前处 B、乙车的平均速度是 C、在距离A城处,乙车追上甲车 D、乙车比甲车早到B城10. 矩形中, , , 点E是边上的一个动点,连接 , 的角平分线交边于点F,若于M点,连接 , 则的最小值是( )A、 B、 C、 D、5
A、乙车开始行驶时,甲车在乙车前处 B、乙车的平均速度是 C、在距离A城处,乙车追上甲车 D、乙车比甲车早到B城10. 矩形中, , , 点E是边上的一个动点,连接 , 的角平分线交边于点F,若于M点,连接 , 则的最小值是( )A、 B、 C、 D、5二、填空题
-
11. 若有意义,则x的取值范围是;12. 中国数字文化源远流长,“万物莫逃乎数”,“一切皆有定数”…,是古人对自然、社会的一种观察和思考.古籍《孙子算经》中也记录了很多古人发现的数字规律.现在请你根据所学知识观察:(1);(2);(3)根据规律写出第(n)个等式:;13. 如图,在半径为1的上顺次取点A,B,C,D,E,连接 , 若 , , 则扇形与扇形的面积之和为(结果保留)
 14. 已知函数(m为常数)的图形经过点 .(1)、m= .(2)、当时,y的最大值与最小值之和为2,则n的值 .
14. 已知函数(m为常数)的图形经过点 .(1)、m= .(2)、当时,y的最大值与最小值之和为2,则n的值 .三、解答题
-
15. 化简:16. 如图,在平面直角坐标系中,的三个顶点分别是 , , .
 (1)、请画出关于x轴对称的 , 点A、B、C分别对应、、;(2)、将以O为旋转中心,顺时针旋转 , 点A、B、C分别对应、、 , 请画出旋转后的图形 .(3)、直接画出与关于直线对称的对称轴 .17. 科技是国家强盛之基,创新是引领发展的第一动力,某公司响应国家号召,在2023年加大科技创新,革新技术实现产值三连增.第一季度产值总额为1655万元,其中二月份产值为550万元,求一月至三月的月平均增长率.18. 反比例函数与一次函数的图像交于A、B两点,A坐标为
(1)、请画出关于x轴对称的 , 点A、B、C分别对应、、;(2)、将以O为旋转中心,顺时针旋转 , 点A、B、C分别对应、、 , 请画出旋转后的图形 .(3)、直接画出与关于直线对称的对称轴 .17. 科技是国家强盛之基,创新是引领发展的第一动力,某公司响应国家号召,在2023年加大科技创新,革新技术实现产值三连增.第一季度产值总额为1655万元,其中二月份产值为550万元,求一月至三月的月平均增长率.18. 反比例函数与一次函数的图像交于A、B两点,A坐标为 (1)、求出B点坐标;(2)、若是反比例函数图像上的点,是一次函数图像上的点,当点M在点N下方时,判断自变量x的取值范围.19. 某滑雪场建造了全省最长的一条滑雪道,其对外宣传说,此雪道的长度超过500米,春节期间,某校“综合与实践”活动小组的同学利用无人机,根据自己的所学知识,设计了如下测量方案:无人机在距地面高度为450米的点P处测得滑雪道起点B处的俯角为 , 测得滑雪道的终点A处的俯角为(即),沿水平方向由点P飞行525米到达点C处,此时测得起点B处的俯角为 , 其中P、A、B、C均在同一竖直平面内,根据以上数据,该滑雪场的宣传是否属实,请说明理由.
(1)、求出B点坐标;(2)、若是反比例函数图像上的点,是一次函数图像上的点,当点M在点N下方时,判断自变量x的取值范围.19. 某滑雪场建造了全省最长的一条滑雪道,其对外宣传说,此雪道的长度超过500米,春节期间,某校“综合与实践”活动小组的同学利用无人机,根据自己的所学知识,设计了如下测量方案:无人机在距地面高度为450米的点P处测得滑雪道起点B处的俯角为 , 测得滑雪道的终点A处的俯角为(即),沿水平方向由点P飞行525米到达点C处,此时测得起点B处的俯角为 , 其中P、A、B、C均在同一竖直平面内,根据以上数据,该滑雪场的宣传是否属实,请说明理由.(参考数据 , , , )
 20. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.
20. 如图,以为直径的经过的顶点 , , 分别平分和 , 的延长线交于点 , 连接.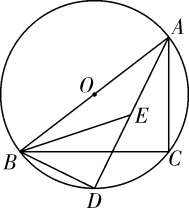 (1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.21. 学校开展“校园读书月”活动,收到了良好的效果.随机调查部分同学,将读0本书、1本书、2本书、3本书、4本书的人数用条形统计图和扇形统计图统计如下:
(1)、判断的形状,并证明你的结论;(2)、若 , , 求的长.21. 学校开展“校园读书月”活动,收到了良好的效果.随机调查部分同学,将读0本书、1本书、2本书、3本书、4本书的人数用条形统计图和扇形统计图统计如下: (1)、本次调查的样本容量是 , 中位数是;(2)、补全条形统计图 , 并完成扇形统计图的填空:m= , n=;(3)、按照上面调查结果,试估计在开展“校园读书月”活动期间,该校2000位学生共阅读了多少本书?22. 问题背景:如图1,在等腰中, , , 垂足为点D,在中, , , 连接中点,连接 , 在绕点A旋转过程中,线段之间存在怎样的数量关系?
(1)、本次调查的样本容量是 , 中位数是;(2)、补全条形统计图 , 并完成扇形统计图的填空:m= , n=;(3)、按照上面调查结果,试估计在开展“校园读书月”活动期间,该校2000位学生共阅读了多少本书?22. 问题背景:如图1,在等腰中, , , 垂足为点D,在中, , , 连接中点,连接 , 在绕点A旋转过程中,线段之间存在怎样的数量关系?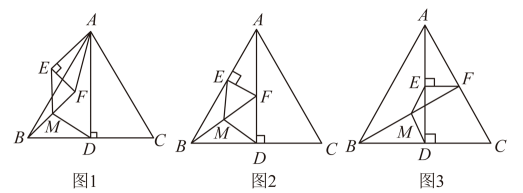 (1)、 观察发现:
(1)、 观察发现:为了探究线段和之间的数量关系,可先将图形位置特殊化,将绕点A旋转,使重合,如图2,易知和之间的数量关系为;
(2)、 操作证明:继续将绕点A旋转,使与重合时,如图3,(1)中线段之间的数量关系仍然成立,请加以证明.
(3)、 问题解决:根据上述探究的经验,我们回到一般情况,如图1,在其他条件不变的情况下,上述的结论还成立吗?请说明你的理由.
23. 如图,某数学兴趣小组以楼梯为场景设计的小球弹射实验示意图,楼梯平台宽为3,前方有六个台阶(各拐点均为90°),每个台阶的高为2,宽为2,楼梯平台到x轴距离 , 从y轴上的点C处向右上方弹射出一个小球P(小球视为点),飞行路线为抛物线 , 当点P落到台阶后立即弹起,其飞行路线是与L形状相同的抛物线. (1)、通过计算判断小球P第一次会落在哪个台阶上;(2)、若小球P第二次的落点在台阶中点M上,求小球P第二次飞行路线的解析式;(3)、若小球P再次从点M处弹起后落入x轴上一圆柱形小球接收装置(小球落在圆柱形边沿也为接收),接收装置最大截面为矩形 , 点E横坐标为16, , , 求出小球第三次飞行路线的顶点到x轴距离最小值.
(1)、通过计算判断小球P第一次会落在哪个台阶上;(2)、若小球P第二次的落点在台阶中点M上,求小球P第二次飞行路线的解析式;(3)、若小球P再次从点M处弹起后落入x轴上一圆柱形小球接收装置(小球落在圆柱形边沿也为接收),接收装置最大截面为矩形 , 点E横坐标为16, , , 求出小球第三次飞行路线的顶点到x轴距离最小值.