安徽省滁州市定远县2023年城西六校中考二模数学试卷
试卷更新日期:2023-05-17 类型:中考模拟
一、单选题
-
1. x的相反数是 , 则x的倒数为( )A、 B、3 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 我国神舟十三号载人飞船和航天员乘组于2022年4月16日返回地球,结束了183天的在轨飞行时间.从2003年神舟五号载人飞船上天以来,我国已有13位航天员出征太空,绕地球飞行共约2.32亿公里.将数据2.32亿用科学记数法表示为( )A、 B、 C、 D、4. 下图所示的几何体是由若干个大小相同的小立方块搭成的,则这个几何体从左面看到的形状图为( )
 A、
A、 B、
B、 C、
C、 D、
D、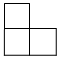 5. 如图,直线a∥b , 在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠B的度数为( )
5. 如图,直线a∥b , 在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠B的度数为( )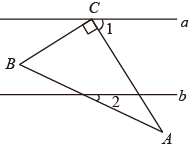 A、56° B、34° C、36° D、24°6. 若样本 , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、平均数为 , 方差为 D、平均数为 , 方差为7. 一次函数y=2x+1的图像不经过 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,在中, , , , 点P为边上任意一点,连接 , 以 , 为邻边作 , 连接 , 则长度的最小值为( )
A、56° B、34° C、36° D、24°6. 若样本 , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、平均数为 , 方差为 D、平均数为 , 方差为7. 一次函数y=2x+1的图像不经过 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图,在中, , , , 点P为边上任意一点,连接 , 以 , 为邻边作 , 连接 , 则长度的最小值为( )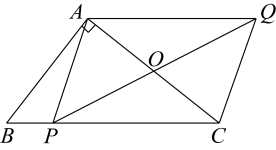 A、 B、 C、 D、9. 设 , , 其中a为实数,则M与N的大小关系是( )A、 B、 C、 D、10. 在同一直角坐标系中,一次函数与二次函数的图像可能是( )A、
A、 B、 C、 D、9. 设 , , 其中a为实数,则M与N的大小关系是( )A、 B、 C、 D、10. 在同一直角坐标系中,一次函数与二次函数的图像可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 分解因式: .12. 如图,在边长为4的等边△ABC中,以B为圆心、BA为半径画弧,再以AB为直径画半圆,则阴影部分的面积为.
 13. 如图,将反比例函数的图像绕原点O逆时针旋转得到曲线 , 点A是曲线上的一点,点B在直线上,连接、 , 若 , 则的面积为.
13. 如图,将反比例函数的图像绕原点O逆时针旋转得到曲线 , 点A是曲线上的一点,点B在直线上,连接、 , 若 , 则的面积为.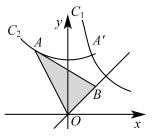 14. 如图,矩形的边 , E是上一点, , F是上一动点,M、N分别是的中点,则的最小值是 .
14. 如图,矩形的边 , E是上一点, , F是上一动点,M、N分别是的中点,则的最小值是 .
三、解答题
-
15. 解不等式组并求它的所有的非负整数解.16. 计算:(1)、;(2)、 .17. 如图,是由小正方形组成的网格,每个小正方形的顶点叫做格点的三个顶点都是格点D是与网格线的交点仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
 (1)、在图1中,将线段绕点A逆时针旋转得到线段;在上画点N,使 .(2)、图2中,在上取点E,使得∥ , 作点A关于的对称点F.18. 巴川河是铜梁的母亲河,为打造巴川河风光带,现有一段长为米的河道整治任务由A、B两个工程队先后接力完成A工程队每天整治米,B工程队每天整治米,共用时天.(1)、求A、B两工程队分别整治河道多少天?(用二元一次方程组解答)(2)、若A工程队整改一米的工费为元,B工程队整改一米的工费为元,求完成整治河道时,这两工程队的工费共是多少?19. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向上,B在D的北偏西方向上.
(1)、在图1中,将线段绕点A逆时针旋转得到线段;在上画点N,使 .(2)、图2中,在上取点E,使得∥ , 作点A关于的对称点F.18. 巴川河是铜梁的母亲河,为打造巴川河风光带,现有一段长为米的河道整治任务由A、B两个工程队先后接力完成A工程队每天整治米,B工程队每天整治米,共用时天.(1)、求A、B两工程队分别整治河道多少天?(用二元一次方程组解答)(2)、若A工程队整改一米的工费为元,B工程队整改一米的工费为元,求完成整治河道时,这两工程队的工费共是多少?19. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向上,B在D的北偏西方向上.
参考数据: , , .
(1)、求证:;(2)、求A,B两点间的距离.20. 春节期间,小颖同学计划跟随父母来西安旅游,决定采用抽签的方式从“1-大唐不夜城现代唐人街”,“2-大唐芙蓉园”,“3-大明宫”,“4-西安明城墙景区”,“5-大唐西市”中选择两个地方去游览,抽签规则如下:把五个地点分别写在五张背面相同的卡片的正面,然后背面朝上放在水平桌面上搅匀后,随机抽取一张,不放回,再抽取一张.(1)、小颖随机抽取一张卡片,抽取到的地点是“大唐不夜城现代唐人街”的概率为;(2)、请用画树状图或列表的方法,求小颖选择去大唐不夜城现代唐人街和大唐芙蓉园这两个地方的概率.21. 已知,如图,△ABC的顶点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°. (1)、若⊙O半径为3,求弦CD的长;(2)、若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
(1)、若⊙O半径为3,求弦CD的长;(2)、若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
