鲁教版（五四制）2022-2023学年度第二学期六年级数学 角的比较 期末复习

试卷更新日期：2023-05-17 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 在同一平面内，若∠A与∠B的两边分别平行，且∠A比∠B的3倍少40°，则∠A的度数为（   ）
    A、20° B、55° C、20°或125° D、20°或55°

    查看试题解析

  • 2. 如图，OB平分∠AOD，OC平分∠BOD，∠AOC＝45°，则∠BOC＝（   ）

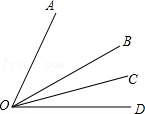    A、5° B、10° C、15° D、20°

    查看试题解析

  • 3. 如图，在△ABC中∠ABC＝60°，点C在直线b上，若直线a∥b，∠2＝26°，则∠1的度数为（   ）

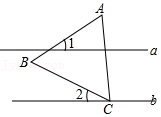    A、26° B、28° C、34° D、36°

    查看试题解析

  • 4. 如图，E是直线CA上一点，∠FEA＝40°，射线EB平分∠CEF，GE⊥EF．则∠GEB＝（   ）

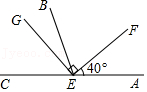    A、10° B、20° C、30° D、40°

    查看试题解析

  • 5. 一把三角尺和一把直尺如图摆放，已知∠BAC是直角，且∠BAC的顶点A在直尺的边DE上，那么在下列结论中，不一定成立的（   ）

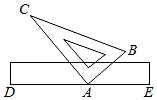    A、∠BAE与∠CAD互余 B、∠BAD＝∠CAE   C、∠CAE＞∠BAE D、∠BAE＝180°﹣∠CAD﹣∠CAB

    查看试题解析

  • 6. 如图，现将一块三角板的含有60°的角的顶点放在直尺的一边上，若∠1＝80°，那么∠2的度数为（   ）

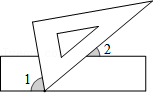    A、30° B、40° C、50° D、60°

    查看试题解析

  • 7. 如图，AB∥CD∥EF，BC∥AD，AC平分∠BAD，则图中与∠AGE相等的角（   ）

    A、2个 B、3个 C、4个 D、5个

    查看试题解析

  • 8. 如图，已知∠AOB与∠EO′F，分别以O，O′为圆心，以同样长为半径画弧，分别交OA，OB于点A′，B′，交O′E，O′F于点E′，F′，以B′为圆心，以E′F′长为半径画弧，交弧A′B′于点A″．下列结论错误的是（   ）

    A、∠AOB＝2∠EO′F B、∠AOB＞∠EO′F C、∠A″OB＝∠EO′F D、∠AOA″＝∠AOB﹣∠EO′F

    查看试题解析

  • 9. 如图，直线AB、CD相交于点O，OE平分∠AOD，若∠1＝38°，则∠COE等于（   ）。

    A、66° B、76° C、109° D、144°

    查看试题解析

  • 10. 如图，已知AD∥BC，∠B＝30°，DB平分∠ADE，则∠DEC＝（   ）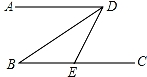

    A、30° B、60° C、90° D、120°

    查看试题解析

二、填空题

  • 11. 如图，点O在直线AE上，射线OC平分∠AOE．如果∠DOB＝90°，∠1＝25°，那么∠AOB的度数为 ．

    查看试题解析

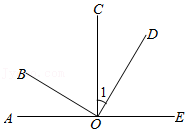  • 12. 如图所示，将长方形纸片ABCD进行折叠，如果∠BHG＝70°，那么∠BHE＝度．

    查看试题解析

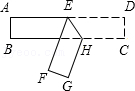  • 13. 如图，若AB∥CD，EF与AB、CD分别相交于点E、F，EP与∠EFD的平分线相交于点P，且∠EFD＝60°，EP⊥FP，则∠BEP＝度．

    查看试题解析

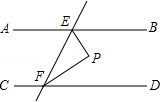  • 14. 如图，∠AOB＝72°，OC平分∠AOB，OD⊥OC，那么∠AOD＝°．

    查看试题解析

  • 15. 如图，点A、O、B在一条直线上，且∠AOD＝35°，OD平分∠AOC，则图中∠BOC＝度．

    查看试题解析

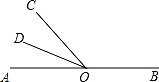
三、解答题

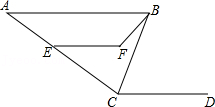
  • 16. 如图，AB∥CD，CB平分∠ACD，∠ACD＝140°，∠CBF＝20°，∠EFB＝130°．求∠CEF的度数．

    查看试题解析

  • 17. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面AB与水杯下沿CD平行，光线EF从水中射向空气时发生折射，光线变成FH，点G在射线EF上，已知∠HFB＝20°，∠FED＝45°，求∠GFH的度数．

    查看试题解析

  • 18. 如图，已知AB∥CD，点M为平面内一点，AM⊥DM于点M．过点M作MG⊥AB于点G，延长GM交CD于N，请说明∠AMG＝∠MDC．

    查看试题解析

四、综合题

  • 19. 如图，∠AFD＝∠1，AC∥DE．

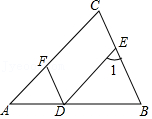    (1)、试说明：DF∥BC；
    (2)、若∠1＝68°，DF平分∠ADE，求∠B的度数．

    查看试题解析

  • 20. 如图，已知∠AOB＝58°，∠AOC在∠AOB外部，ON、OM分别平分∠AOC、∠BOC．

    (1)、若∠AOC＝32°，则∠MON＝；
    (2)、若∠AOC＝n°（0＜n＜90°），ON、OM依旧分别平分∠AOC、∠BOC，∠MON的大小是否改变？；
    (3)、试说明（2）的结论的理由．

    查看试题解析

  • 21. 如图，已知点O是直线AB上的一点．

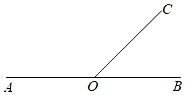    (1)、利用直尺和圆规分别作出∠BOC的角平分线OD和∠AOC的角平分线OE，保留作图痕迹；
    (2)、若∠BOC＝40°，求∠AOE的度数；
    (3)、∠COE有补角吗？若有，请把它找出来，并说明理由．

    查看试题解析

  • 22. 如图所示，∠AOB是平角，∠AOC＝30°，∠BOD＝60°，OM、ON分别是∠AOC、∠BOD的平分线．求：

    (1)、∠COD的度数；
    (2)、求∠MON的度数．

    查看试题解析

  • 23. 已知：如图1，直线AB、CD被直线MN所截，且AB∥CD．点E在直线AB、CD之间的线段MN上，P、Q分别在直线AB、CD上，连接PE、EQ．

    (1)、小明探究发现：∠PEQ＝∠APE+∠CQE，请你帮小明说明理由；
    (2)、如图2，已知∠FPB＝ 12 ∠EPB，∠FQD＝ 12 ∠EQD，若∠PEQ＝80°，请你利用小明发现的结论求∠PFQ的度数；
    (3)、如图3，若∠FPB＝ 13 ∠EPB，∠FQD＝ 13 ∠EQD，请你直接写出∠PEQ和∠PFQ之间的数量关系．

    查看试题解析