鲁教版（五四制）2022-2023学年度第二学期六年级数学 比较线段的长短 期末复习
试卷更新日期：2023-05-17 类型：复习试卷
一、单选题
-
1. 把弯曲的公路改直，能够缩短行程，这样做的道理是（ ）A、两点确定一条线段 B、两点确定一条直线 C、两点之间线段最短 D、两点之间直线最短2. 下列说法不正确的个数有（ ）
①经过两点有一条直线，且只有一条直线；②常数项的同类项还是常数项；
③a+b= a-(-b)；④连接两点间的线段，叫做这两点的距离；
⑤如果线段AB=BC，则点B是线段AC的中点．
A、2个 B、3个 C、4个 D、5个3. 两根木条，一根长10cm，另一根长12cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为（ ）A、1cm B、11cm C、1cm 或11cm D、2cm或11cm4. 如图，点P是直线a外的一点，点A、B、C在直线a上，且PB⊥a，垂足是B，PA⊥PC，则下列正确的语句是（ ）
A、线段PC的长是点P到直线a的距离 B、PA，PB，PC三条线段中，PB最短 C、线段AC的长是点A到直线PC的距离 D、线段AC的长是点C到直线PA的距离5. 如图，已知AB＝10cm，点C在线段AB上，且AC＝6cm，点E是线段AC的中点，点D是线段BC的中点．则DE的长为（ ）
A、4cm B、5cm C、6cm D、7cm6. 下列说法正确的是（ ）。A、延长射线AB到C B、若AM＝BM，则M是线段AB的中点 C、两点确定一条直线 D、过三点能作且只能作一条直线7. 把弯曲的道路改直就能缩短路程，下列数学语言解释正确的是（ ）A、垂线段最短 B、两点确定一条直线 C、两点之间线段最短 D、对顶角相等8. 如图，已知线段 ， ， 画一条射线 ， 在射线上依次截取 ， 在线段上截取.则（ ）
A、 B、 C、 D、9. 数轴上有一个点B表示的数是3，点C到点B的距离为2个单位长度，则点C表示的数为（ ）A、1 B、5 C、3或2 D、1或510. 已知线段AB＝8，BC＝3，且A，B，C三点在同一条直线上，则AC的长是（ ）A、5 B、11 C、5或11 D、24二、填空题
-
11. 已知线段AB=12，C是线段AB上一点，且BC=2，点D在射线AB上，若DA=4DC，则BD的长为.12. 如图，点C、D、E在线段AB上，若点C是线段AB的中点，DB=3BE，AB=CD， CE=23，则AB=
13. 如图，已知AB和CD的公共部分BD＝ AB＝ CD，线段AB，CD的中点E，F之间的距离是10cm，则AB的长是 ．
14. 如图，点B在线段上，已知 ， ， 点O是线段的中点，则线段cm.
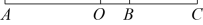15. A、B、C三点在同一条直线上，AB=6cm，BC=2cm，则AC=.三、解答题
-
16. 已知点 ， ， 在直线上，点 ， 分别为线段 ， 的中点，线段的长度为 ， 线段的长度为.请画出示意图，并求出线段的长.17. 如图，点C把线段MN分成两部分，其比为MC：CN=5：4，点P是MN的中点，PC=2cm，求MN的长．
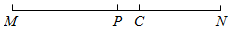18. 已知点C是线段AB的中点，点D是线段AB上一点，且CD＝ ，若AD＝4，求AB长度．四、综合题
-
19. 如图，O为原点，在数轴上A点表示的有理数为a， B点表示的有理数为b，AB表示A点和B点的距离，且(a-6)2+|b+4|=0．
(1)、直接写出a，b的值及AB的长度．a= ， b= ， AB=。(2)、若动点P从点A出发，以每秒3个单位长度的速度沿数轴向左匀速运动，动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、点Q同时出发，设点P、点Q的运动时间为t秒，诸用含t的式子表示PQ的长；(3)、在(2)的条件下，N是AB中点，M是PQ中点，是否存在这样的$，使ON=2OM，若存在、请求出t的值：若不存在，请说明理由．20. 如图，点 C，E 是线段 AB 上两点，点 D 为线段 AB 的中点，AB＝6，CD＝1．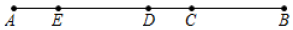
(1)、求 BC 的长；(2)、若 AE：EC＝1：3，求 EC 的长．21. 如图，点O为数轴原点，点A对应的数为-5，点B对应的数为10.
(1)、点C是数轴上A、B之间的一个点，且 ， 求线段CA的长及点C对应的数.(2)、点P从点A出发以每秒2个单位的速度沿数轴正方向运动，点Q从点B出发以每秒1个单位的速度沿数轴负方向运动.P、Q两点同时出发，设运动时间为t秒.当满足 ， 求运动时间t.
