人教版七年级下数学期末复习知识点扫盲满分计划——8.3实际问题与二元一次方程组一-在线组卷题库

1. 如图，在周长为60的长方形ABCD中放入六个相同的小长方形，若小长方形的面积为S，长为x，宽为y，则（）

A、若x＝2，则S＝20 B、若y＝2，则S＝20 C、若x＝2y，则S＝10 D、若x＝4y，则S＝10

查看试题解析
2. 如图，三个形状，大小都相同的小长方形沿“横—竖—横”排列在一个大长方形中，若这个大长方形的周长为2016cm，则一个小长方形的周长为cm．

查看试题解析
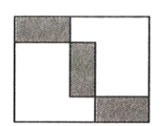3. 如图，是由截面为同一种长方形的墙砖粘贴的部分墙面，其中三块横放的墙砖比两块竖放的墙砖低30cm，两块竖放的墙砖比两块横放的墙砖高50cm，则每块墙砖的截面面积是

查看试题解析
4. 塑料凳子轻便实用，人们生活中随处可见．如图，3 支塑料凳子叠放在一起的高度为55cm，5 支塑料凳子叠放在一起的高度为 65cm，当有 10 支塑料凳子整齐地叠放在一起时，其高度是cm．

查看试题解析
5. 如图所示，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的 $\frac{1}{3}$ ，另一根露出水面的长度是它的 $\frac{1}{5}$ .两根铁棒长度之和为220cm，此时木桶中水的深度是cm.

查看试题解析

6. 秋天到了，花溪区高坡乡美景如画，其中露营基地吸引了不少露营爱好者，露营基地为了接待30名露营爱好者，需要搭建可容纳3人或2人的帐篷若干，若所搭建的帐篷恰好能容纳这30名露营爱好者，则不同的搭建方案有种.

查看试题解析
7. 在今年的亚运会召开期间，大批的学生志愿者参与服务工作．学校计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位．

(1)、计划调配36座新能源客车多少辆？该学校共有多少名志愿者？

(2)、若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？

查看试题解析
8. 今年疫情期间某物流公司计划用两种车型运输救灾物资，用2辆A型车和1辆B型车装满物资一次可运10吨；用1辆A型车和2辆B型车一次可运11吨．某物流公司现有31吨货物资，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满．

(1)、1辆A型车和1辆B型车都装满物资一次可分别运多少吨？

(2)、请你帮该物流公司设计租车方案，并把符合要求的租车方案都列出来；

(3)、若A型车每辆需租金每次100元，B型车每辆租金每次120元，请从（2）中的方案里选出最省钱的租车方案，并求出最少租车费．

查看试题解析
9. 一方有难，八方支援．“新冠肺炎”疫情来袭，除了医务人员主动请缨走向抗疫前线，众多企业也伸出援助之手，某公司用甲、乙两种货车向武汉运送爱心物资，两次满载的运输情况如表：

甲种货车（辆）
乙种货车（辆）
物资总量（吨）
第一次
2
1
10
第二次
1
2
11

(1)、甲、乙两种货车每辆分别能装货多少吨？

(2)、现有31吨物资需要再次运往武汉，准备同时租用这两种货车，每辆均全部装满货物，问有哪几种租车方案？

查看试题解析
10. 某电脑公司有A型、B型、C型三种型号电脑，其中A型每台6000元，B型每台4000元，C型每台2500元，某中学现有资金100500元，计划全部用于从这家电脑公司购进36台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择，并说明理由.

查看试题解析

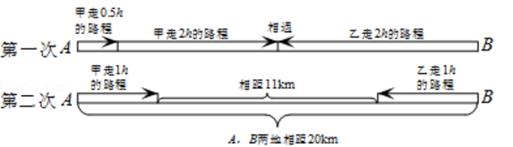
11. 小明郊游时，早上9时下车，先走平路然后登山，到山顶后又沿原路返回到下车处，正好是下午2时．若他走平路每小时行4km，爬山时每小时走3km，下山时每小时走6km，小明从上午到下午一共走的路程是（）

A、5km B、10km C、20km D、答案不唯一

查看试题解析
12. 从甲地到乙地的路有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地用54分钟，从乙地到甲地用42分钟，甲地到乙地的全程是多少？

查看试题解析
13. 一条船顺流航行，每小时行 $25 k m$ ；逆流航行，每小时行 $17 k m$ ．设轮船在静水中的速度为 $x k m / h$ ，水的流速为 $y k m / h$ ．根据题意，得到的方程组是（）

A、 ${\begin{array}{l} x + y = 25 \\ y + x = 17 \end{array}$ B、 ${\begin{array}{l} x - y = 17 \\ x = 25 + y \end{array}$ C、 ${\begin{array}{l} x - 25 = y \\ x + y = 17 \end{array}$ D、 ${\begin{array}{l} x + y = 25 \\ x - y = 17 \end{array}$

查看试题解析
14. 甲乙二人分别从相距20km的A，B两地出发，相向而行．如图是小华绘制的甲乙二人运动两次的情形，设甲的速度是xkm／h，乙的速度是ykm／h，根据题意可列出方程组．

查看试题解析
15. 甲、乙两人练习跑步，若乙先跑8米，则甲跑4分钟可追上乙；若乙先跑2分钟，则甲跑5分钟可追上乙．若设甲的速度为x米/分，乙的速度为y米/分，则下列列出的方程组中正确的是（　　）

A、 $\{\begin{matrix} 4 x = 4 y + 8 \\ 5 x = 2 y + 5 y \end{matrix}$ B、 $\{\begin{matrix} 4 x + 8 = 4 y \\ 5 x = 5 y + 2 y \end{matrix}$ C、 $\{\begin{matrix} 4 x = 4 y + 8 \\ 5 x = 5 y - 2 y \end{matrix}$ D、 $\{\begin{matrix} 4 x + 8 = 4 y \\ 5 x + 2 y = 5 y \end{matrix}$

查看试题解析

16. 阅读理解：
为打造陶子河沿岸的风景带，有一段长为360米的河道整治任务由A、B两个工程队先后接力完成，A工程队每天整治24米，B工程队每天整治16米，共用20天.

(1)、根据题意，甲乙两个同学分别列出了尚不完整的方程组如下：
甲： ${\begin{array}{l} x + y =_________ \\ 24 x + 16 y =_________ \end{array}$             乙： ${\begin{array}{l} x + y =_________ \\ \frac{x}{24} + \frac{y}{16} =_________ \end{array}$

根据甲、乙两名同学所列的方程组，请你分别指出未知数 $x$ ， $y$ 表示的意义，并且补全甲、乙两名同学所列的方程组：

甲： $x$ 表示      ▲       ， $y$ 表示      ▲      ；

乙： $x$ 表示      ▲       ， $y$ 表示      ▲      ；

(2)、求出其中一个方程组的解，并回答A、B两工程队分别整治河道多少米？

查看试题解析
17. 为打造单县东沟河河道风光带，现有一段长为180米的河道整治任务，由A，B两个工程小组先后接力完成， $A$ 工程小组每天整治12米，B工程小组每天整治 $8$ 米，共用时20天，设 $A$ 工程小组整治河道 $x$ 米， $B$ 工程小组整治河道 $y$ 米，依题意可列方程组（）

A、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 180 \\ \frac{x}{12} + \frac{y}{8} = 20 \end{array}$ B、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 20 \\ 12 x + 8 y = 20 \end{array}$ C、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 20 \\ \frac{x}{12} + \frac{y}{8} = 180 \end{array}$ D、 ${\begin{cases} \end{cases} \begin{array}{l} x + y = 180 \\ \frac{12}{x} + \frac{8}{y} = 20 \end{array}$

查看试题解析
18. 永川区某工程公司积极参与“三城同创”建设，该工程公司下属的甲工程队、乙工程队分别承包了三城的A工程、B工程，甲工程队睛天需要14天完成，雨天工作效率下降30%；乙工程队晴天需15天完成，雨天工作效率下降20%，实际上两个工程队同时开工，同时完工，两个工程队各工作了天.

查看试题解析
19. 某建设工程队计划每小时挖掘土石方 $540$ 方，现决定租用甲、乙两种型号的挖掘机来完成这项工作，已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土 $140$ 方， $5$ 台甲型挖掘机与 $3$ 台乙型挖掘机恰好能完成每小时的挖掘量.

(1)、求甲、乙两种型号的挖掘机每小时各挖土多少方？

(2)、若租用一台甲型挖掘机每小时 $100$ 元，租用一台乙型挖掘机每小时 $120$ 元，且每小时支付的总租金不超过 $850$ 元，又恰好完成每小时的挖掘量，请设计该工程队的租用方案.

查看试题解析
20. 某建设工程队计划每小时挖掘土540方，现决定租用甲、乙两种型号的挖掘机来完成这项工作，已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土140方，5台甲型挖掘机与3台乙型挖掘机恰好能完成每小时的挖掘量.

(1)、求甲、乙两种型号的挖掘机每小时各挖土多少方？

(2)、若租用一台甲型挖掘机每小时100元，租用一台乙型挖掘机每小时120元，且每小时支付的总租金不超过850元，又恰好完成每小时的挖掘量，请设计该工程队的租用方案.

查看试题解析

21. 为安置50名培训人员入住，需要同时租用6人间和4人间两种客房，若每个房间都住满，则租房方案共有（）

A、4种 B、5种 C、6种 D、7种

查看试题解析
22. 某校有两种类型的学生宿舍30间，大宿舍每间可住8人，小宿舍每间可住5人．该校198个住宿生恰好住满30间宿舍．设大宿舍有x间，小宿舍有y间，得方程组：（）

A、 ${\begin{array}{l} 5 x + 8 y = 198 \\ x + y = 30 \end{array}$ B、 ${\begin{array}{l} 8 x + 5 y = 198 \\ x + y = 30 \end{array}$ C、 ${\begin{array}{l} x + y = 198 \\ 8 x + 5 y = 30 \end{array}$ D、 ${\begin{array}{l} x + y = 198 \\ 5 x + 8 y = 30 \end{array}$

查看试题解析
23. 3月12日是我国的植树节．这一天，某校七年级共有240名学生参加义务植树活动．如果平均每人每天挖树坑6个或栽树10课，那么，怎样安排学生才能使这一天挖出的树坑全部栽上树苗？（要求列方程组解答）

查看试题解析
24. 某汽车制造厂开发了一款新式电动汽车计划一年生产安装240辆，由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人；他们经过培训后上岗，也能独立进行电动汽车的安装.生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车.

(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车?

(2)、如果工厂抽调熟练工m名，再招聘 $n (0 < n < 10)$ 名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案?

查看试题解析
25. 新冠病毒来势汹汹，疫情刻不容缓，某企业接到一批制氧机订单急需大量工人生产制氧机，该企业招聘了一些工人，按照熟练程度，分为一级、二级、三级，已知一名一级工人和三名三级工人共同生产3天可完成54台，且一名一级工人每天比一名三级工人每天多生产6台。

(1)、求每名一级工人和每名三级工人每天分别生产多少台制氧机？

(2)、为了最大限度提高产量，该企业决定每月花费90000元（全部用完）招聘一、二、三级工人合计18人，其中各级工人至少一人，已知二级工人每天生产量是三级工人的2倍，一级、二级、三级工人每月的工资分别是6000元，5000元，3500元，问该企业应如何安排招聘方案，使得每天生产制氧机的台数最多？最多为多少台？

查看试题解析

26. 对于一个三位数 $n$ ，如果 $n$ 满足∶ 它的百位数字、十位数字之和与个位数字的差等于 7 ，那么称这个数 $n$ 为 “幸福数”. 例如∶ $n_{1} = 722 ， ∵ 7 + 2 - 2 = 7 ， ∴ 722$ 是“幸福数”； $n_{2} = 913 ， ∵ 9 + 1 - 3 = 7 ， ∴ 913$ 是“幸福数”； $n_{3} = 285 ， ∵ 2 + 8 - 5 \neq 7 ， ∴ 285$ 不是“幸福数”. 若将一个“幸福数” $m$ 的个位数的 2 倍放到十位，原来的百位数变成个位数，原来的十位数变成百位数，得到一个新的三位数 $t$ (例如∶ 若 $m = 654$ ，则 $t = 586$ )，若 $t$ 也是一个“幸福数”，则满足条件的所有 $m$ 的值.

查看试题解析
27. 在一个3×3的方格中填写9个数字，使得每行每列每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．如图所示的方格中填写了一些数和字母，为使该方格构成一个三阶幻方，则x+2y的值是（）
﹣3
y

1

4
x

A、15 B、17 C、19 D、21

查看试题解析
28. 在《九章算术》中，一次方程组是由算筹布置而成的．如图1所示的算筹图，表示的方程组就是 ${\begin{cases} 2 x + y = 11 ， \\ 4 x + 3 y = 27 ， \end{cases}$ 类似地，图2所示的算筹图表示的方程组为（）

A、 ${\begin{cases} 3 x + 2 y = - 14 ， \\ x + 4 y = 23 \end{cases}$ B、 ${\begin{cases} 3 x + 2 y = - 9 ， \\ x + 4 y = 23 \end{cases}$ C、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 3 \end{cases}$ D、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 23 \end{cases}$

查看试题解析
29. 一个两位数，若交换其个位数与十位数的位置，则所得新两位数比原两位数大45，这样的两位数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
30. 甲是乙现在的年龄时，乙8岁；乙是甲现在的年龄时，甲20岁，则（）

A、甲比乙大6岁 B、乙比甲大6岁 C、甲比乙大4岁 D、乙比甲大4岁

查看试题解析

31. 为实现营养的合理搭配，某电商推出适合不同人群的甲、乙两种袋装混合粗粮．其中，甲种粗粮每袋装有3千克 $A$ 粗粮，1千克 $B$ 粗粮，1千克 $C$ 粗粮；乙种粗粮每袋装有1千克 $A$ 粗粮，2千克 $B$ 粗粮，2千克 $C$ 粗粮．甲、乙两种袋装粗粮每袋成本价分别为袋中的 $A$ ， $B$ ， $C$ 三种粗粮的成本价之和．已知 $A$ 粗粮每千克成本价为 $6$ 元，甲种粗粮每袋售价为58.5元，利润率为30%，乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%，则该电商销售甲、乙两种袋装粗粮的数量之比是.（商品的利润率 $= \frac{商品的售价 - 商品的成本价}{商品的成本价} \times 100 %$ ）

查看试题解析
32. 某鞋店正举办开学特惠活动，如图为活动说明.
小彻打算在该店同时购买一双球鞋及一双皮鞋，且他有一张所有购买的商品定价皆打8折的折价券.若小彻计算后发现使用折价券与参加特惠活动两者的花费相差50元，则下列叙述何者正确？（）

A、使用折价券的花费较少，且两双鞋的定价相差100元 B、使用折价券的花费较少，且两双鞋的定价相差250元 C、参加特惠活动的花费较少，且两双鞋的定价相差100元 D、参加特惠活动的花费较少，且两双鞋的定价相差250元

查看试题解析
33. 某水果店计划进A，B两种水果共100千克，这两种水果的进价和售价如表所示．

进价（元/千克）

售价（元/千克）

A种水果

5

8

B种水果

9

13

(1)、若该水果店购进这两种水果共花费740元，求该水果店分别购进A，B两种水果各多少千克？

(2)、在（1）的基础上，为了促销，水果店老板决定把A种水果全部八折出售，B种水果全部降价10%出售，那么售完后共获利多少元？

查看试题解析

34. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	4台	1200元
第二周	5台	6台	1900元

(进价、售价均保持不变，利润=销售收入-进货成本)

(1)、求A、B两种型号的电风扇的销售单价；

(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台?

(3)、在(2)的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标?若能，请给出相应的采购方案；若不能，请说明理由。

查看试题解析

35. 某校组织“大手拉小手，义卖献爱心”活动，购买了黑白两种颜色的文化衫共140件，进行手绘设计后出售，所获得利润全部捐给山区困难孩子．每件文化衫的批发价和零售价如下表：

批发价（元）
零售（元）
黑色文化衫
10
a
白色文化衫
8
b

(1)、当 $a = 24$ ， $b = 20$ ，假设文化衫全部售出，共获利1860元，求黑白两种文化衫各多少件？

(2)、假设文化衫全部售出，其中卖出了黑色文化衫60件，要获得1900元，请求出b与a的关系式．

查看试题解析

36. 在世界杯足球赛中，32支足球队将分为8个小组进行单循环比赛，小组比赛规则如下：胜一场得3分，平一场得1分，负一场得0分.若小组赛中某队的积分为5分，则该队必是（）

A、两胜一负 B、一胜两平 C、一胜一平一负 D、一胜两负

查看试题解析
37. 在某次知识竞赛中，甲、乙两人轮流答题，每人都要回答20道题，每道题回答符合题意得m分，回答不符合题意或放弃回答扣n分．当甲、乙两人恰好都答完12道题时，甲答对了9道题，得分为45分；乙答对了10道题，得分为54分．

(1)、求m和n的值；

(2)、假如最后得分不低于70分就能晋级，甲在剩下的比赛中至少还要答对多少道题才能顺利晋级？

查看试题解析
38. 校园举行足球比赛，胜一场得3分，平一场得1分，输一场得0分；七年一班共进行了12场比赛，获得19分，则七年一班获胜的场数有几种情况（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
39. 小明、小颖、小亮玩飞镖游戏，他们每人投靶 $5$ 次，中靶情况如图所示．规定投中同一圆环得分相同，若小明得分 $21$ 分，小亮得分 $17$ 分，则小颖得分为（）

A、 $19$ 分 B、 $20$ 分 C、 $21$ 分 D、 $22$ 分

查看试题解析
40. 在一次数学知识竞赛中，共有20道题，规定：答错或不答一道题扣分相同，当答题结束时，A同学答对14道题，得分为58分；B同学答对11道题，得分为37分．请问答对一道题得几分，答错或不答一道题扣几分．

查看试题解析

人教版七年级下数学期末复习知识点扫盲满分计划——8.3实际问题与二元一次方程组一

一、几何问题

二、方案问题

三、行程问题

四、工程问题

五、分配问题

六、数字和年龄问题

七、销售利润问题

八、积分问题

	甲种货车（辆）	乙种货车（辆）	物资总量（吨）
第一次	2	1	10
第二次	1	2	11

	进价（元/千克）	售价（元/千克）
A种水果	5	8
B种水果	9	13

	批发价（元）	零售（元）
黑色文化衫	10	a
白色文化衫	8	b

﹣3	y
	1
4		x