北师大版2022-2023学年度第二学期八年级数学 三角形的中位线 期末复习
试卷更新日期:2023-05-16 类型:复习试卷
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )
 A、4 B、 C、 D、62. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( )
A、4 B、 C、 D、62. 如图,在中,点 , 分别是 , 边上的中点,连接 , 如果 , 那么的长是( ) A、 B、 C、 D、3. 在中,D、E分别是、的中点,若 , 则的值( )A、3 B、6 C、9 D、244. 如图,在中, , 为中线,延长至点E,使 , 连接 , F为的中点,连接 , 若 , , 则的长为( )
A、 B、 C、 D、3. 在中,D、E分别是、的中点,若 , 则的值( )A、3 B、6 C、9 D、244. 如图,在中, , 为中线,延长至点E,使 , 连接 , F为的中点,连接 , 若 , , 则的长为( )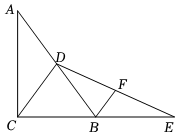 A、 B、 C、 D、5. 如图,在平行四边形中,于点H,E是的中点,F是的中点,已知 , , 则的长为( )
A、 B、 C、 D、5. 如图,在平行四边形中,于点H,E是的中点,F是的中点,已知 , , 则的长为( )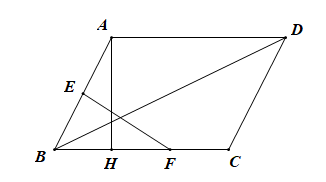 A、 B、 C、 D、6. 如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( )
A、 B、 C、 D、6. 如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( ) A、10 m B、20 m C、5 m D、40 m7. 如图,△ABC中,D,E分别是AB,AC的中点,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为( )
A、10 m B、20 m C、5 m D、40 m7. 如图,△ABC中,D,E分别是AB,AC的中点,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为( )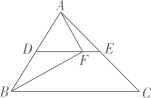 A、3 B、4 C、5 D、68. 如图,在矩形中,交于点 , 点在上,连接交于点 , 且 , 若 , 则的值是 ( )
A、3 B、4 C、5 D、68. 如图,在矩形中,交于点 , 点在上,连接交于点 , 且 , 若 , 则的值是 ( ) A、 B、 C、 D、89. 如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( )
A、 B、 C、 D、89. 如图,在△ABC中,D、E分别是AB、AC边上的中点,若DE=4,则BC等于( ) A、2 B、4 C、8 D、1210. 如图,中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( )
A、2 B、4 C、8 D、1210. 如图,中,AB=10,AC=7,BC=9,点D、E、F分别是AB、AC、BC的中点,则四边形DBFE的周长是( ) A、13 B、 C、17 D、19
A、13 B、 C、17 D、19二、填空题
-
11. 如图,、、、分别为、、、的中点, , 若 , 则四边形的周长.
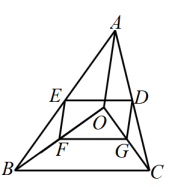 12. 如图,在中,D,E,F分别是 , , 的中点,若 , , 则的周长为.
12. 如图,在中,D,E,F分别是 , , 的中点,若 , , 则的周长为. 13. 如图,在△ABC中,点D,E分别是AB,AC的中点,连结BE,若AE=6,DE=5,∠BEC=90°,则BE=.
13. 如图,在△ABC中,点D,E分别是AB,AC的中点,连结BE,若AE=6,DE=5,∠BEC=90°,则BE=. 14. 如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是m.
14. 如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是m. 15. 如图,在矩形中, , , 分别平分 , 交于点E,F,且 , 相交于点O,连接并延长交于点G.则下面结论正确的是.(写出所有正确结论的序号)
15. 如图,在矩形中, , , 分别平分 , 交于点E,F,且 , 相交于点O,连接并延长交于点G.则下面结论正确的是.(写出所有正确结论的序号)①;
②四边形是轴对称图形;
③;
④.

三、解答题
-
16. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
 17. 如图,在中,D,E,F分别是AB,BC,CA的中点, , , 求四边形DECF的周长.
17. 如图,在中,D,E,F分别是AB,BC,CA的中点, , , 求四边形DECF的周长. 18. 如图,点D、E、F分别是AC、BC、AB中点,连接DE,且BD是的角平分线.求证: .
18. 如图,点D、E、F分别是AC、BC、AB中点,连接DE,且BD是的角平分线.求证: .
四、综合题
-
19. 如图,四边形是正方形,E是边的中点, , 且交正方形外角的平分线于点F.
 (1)、求证:;(2)、连接 , 则的值为;(3)、连接 , 设与交于点H,连接 , 探究之间的关系.20. 如图,在△ABC中,BD平分∠ABC交AC于点D,且BD⊥AC,点F在BC上,点E为AF的中点,连接AF ,BE,ED,DF,BF= DE.
(1)、求证:;(2)、连接 , 则的值为;(3)、连接 , 设与交于点H,连接 , 探究之间的关系.20. 如图,在△ABC中,BD平分∠ABC交AC于点D,且BD⊥AC,点F在BC上,点E为AF的中点,连接AF ,BE,ED,DF,BF= DE. (1)、求证:四边形DEBF是平行四边形.(2)、若AC=DE,BD=6,求AB的长.21. 已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且 , 联结CM、DN.
(1)、求证:四边形DEBF是平行四边形.(2)、若AC=DE,BD=6,求AB的长.21. 已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且 , 联结CM、DN.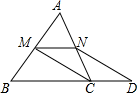 (1)、求证:四边形MCDN是平行四边形;(2)、若三角形AMN的面积等于5,求梯形MBDN的面积.
(1)、求证:四边形MCDN是平行四边形;(2)、若三角形AMN的面积等于5,求梯形MBDN的面积.

