北师大版2022-2023学年度第二学期八年级数学分式的加减法期末复习

试卷更新日期：2023-05-16 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知 $x^{2} - 3 x - m = 0$ ，则代数式 $\frac{x}{x^{2} - x - m}$ 的值是（）

A、3 B、2 C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. 某飞行器在相距为m的甲、乙两站间往返飞行．在没有风时，飞行器的速度为v，往返所需时间为 $t_{1}$ ；如果风速度为 $p (0 < p < v)$ ，则飞行器顺风飞行速度为 $(v + p)$ ，逆风飞行速度为 $(v - p)$ ，往返所需时间为 $t_{2}$ ．则 $t_{1}$ 、 $t_{2}$ 的大小关系为（）

A、 $t_{1} < t_{2}$ B、 $t_{1} \leq t_{2}$ C、 $t_{1} \geq t_{2}$ D、无法确定

查看试题解析
3. 数学课上，老师让计算 $\frac{2 a}{a - b} + \frac{a - 3 b}{a - b}$ ．佳佳的解答如下：
解：原式 $= \frac{2 a + a - 3 b}{a - b}$ ①
$= \frac{3 a - 3 b}{a - b}$ ②
$= \frac{3 (a - b)}{a - b}$ ③
＝3④
对佳佳的每一步运算，依据错误的是（）

A、①：同分母分式的加减法法则 B、②：合并同类项法则 C、③：逆用乘法分配律 D、④：等式的基本性质

查看试题解析
4. 计算 $\frac{2 a}{a + 2} - \frac{a - 2}{2 + a}$ 的结果为（）

A、 $a + 2$ B、 $a - 2$ C、1 D、 $\frac{a - 2}{a + 2}$

查看试题解析
5. 若xy＝x－y，则分式 $\frac{1}{x} - \frac{1}{y} =$ （）

A、 $\frac{1}{x y}$ B、－1 C、y－x D、1

查看试题解析
6. 下面是一位同学做分式运算的过程，M，N代表代数式，则下列关于M、N的式子正确的是（）
$\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4} = \frac{x + 2}{x (x - 2)} - \frac{x - 1}{(x - 2)^{2}} = \frac{M}{x (x - 2)^{2}} - \frac{N}{x (x - 2)^{2}}$

A、 $M = x^{2} - 2$ B、 $N = x^{2} + x$ C、 $M = x^{2} + 4$ D、 $N = x^{2} - x$

查看试题解析
7. 已知关于x不等式组 ${\begin{array}{l} 2 x - 3 a < 2 \\ x - 2 b > 3 \end{array}$ 的解集为 $- 1 < x < 2$ ，则代数式 $(a - \frac{b^{2}}{a}) \cdot \frac{a}{a - b}$ 的值是（）

A、 $\frac{2}{3}$ B、-2 C、 $- \frac{8}{3}$ D、 $- \frac{4}{3}$

查看试题解析
8. 已知， $a + b = 2$ ， $a b = - 5$ 则 $\frac{1}{a} + \frac{1}{b}$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{2}{5}$ C、 $- \frac{5}{2}$ D、 $- \frac{2}{5}$

查看试题解析
9. 如果 $a - b = 1$ ，那么代数式 $(1 - \frac{b^{2}}{a^{2}}) \cdot \frac{2 a^{2}}{a + b}$ 的值是

A、2 B、-2 C、1 D、-1

查看试题解析
10. 如图，若x为正整数，则表示1- $\frac{1}{x 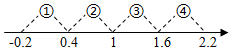+ 1}$ 的值的点落在（）

A、段① B、段② C、段③ D、段④

查看试题解析

二、填空题

11. $\frac{1}{3 y^{2}}$ ， $\frac{4}{x y}$ 和 $\frac{5}{2 x^{2} y}$ 的最简公分母是.

查看试题解析
12. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)} = \frac{A}{x - 1} + \frac{B}{x - 2}$ ，则A^B的值 .

查看试题解析
13. 化简： $\frac{4 x}{x^{2} - 4} - \frac{x}{x - 2} =$ .

查看试题解析
14. 已知 $\frac{1}{x} - \frac{1}{y} = 6$ ，则分式 $\frac{x y}{x - y}$ 的值等于．

查看试题解析
15. 已知，ab=-1，a+b=2，则式子 $\frac{b}{a} + \frac{a}{b}$ =.

查看试题解析

三、解答题

16. 化简 $\frac{x + 1}{x^{2} + 4 x + 4} \div (x - 1 + \frac{2}{x + 2})$ ，再从1，0，-1，-2中选一个喜欢的数求值.

查看试题解析
17. 已知x为整数，且 $\frac{2}{x + 3}$ + $\frac{2}{3 - x}$ + $\frac{2 x + 18}{x^{2} - 9}$ 化简结果为整数，求出所有符合条件的x值．

查看试题解析
18. 先化简，再求值：（ $\frac{2}{x - 3} + \frac{x}{3 - x}$ ） $\div \frac{x - 2}{x^{2} - 6 x + 9}$ ，其中x＝8．

查看试题解析

四、综合题

19. “ $| \begin{array}{l} a & b \\ c & d \end{array} |$ ”称为二阶行列式，规定它的运算法则为： $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，例如： $| \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} | = 1 \times 4 - 2 \times 3 = - 2$ .

(1)、计算 $| \begin{matrix} a + b & a - b \\ \frac{1}{2 a^{2} b} & \frac{1}{2 a^{2} b} \end{matrix} |$ ；

(2)、求等式 $| \begin{array}{l} 2 & \frac{1}{1 - x} \end{array} | = 1$ 中x的值.

查看试题解析
20. 已知a＝， b＝．

(1)、求ab，a＋b的值．

(2)、求＋的值．

查看试题解析
21. 已知代数式 $\frac{1}{x - 1} + \frac{x^{2} - 3 x}{x^{2} - 1}$ ，回答下列问题：

(1)、当x=－2时，化简并求出这个代数式的值；

(2)、小红根据化简的结果认为：“当x=1时，该代数式的值为0”，你同意她的说法吗？请说明理由．

查看试题解析
22.

(1)、①解不等式组 ${\begin{array}{l} 3 (x - 2) + 4 ＜ 5 x \\ \frac{1 - x}{4} + x \geq 2 x - 1 \end{array}$ ，并写出它的非负整数解；
②解方程 $\frac{x}{x - 3} - 2 = \frac{4}{x - 3}$ ；

(2)、先化简 $\frac{2 a + 2}{a - 1} \div (a + 1) + \frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后a在-1、1、2三个数中任选一个合适的数代入求值．

查看试题解析
23. 【阅读材料】若分式A与分式B的差等于它们的积，即 $A - B = A B$ ，则称分式B是分式A的“关联分式”．
例如 $\frac{1}{x + 1}$ 与 $\frac{1}{x + 2}$ ，
解： $∵ \frac{1}{x + 1} - \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ，
$\frac{1}{x + 1} \times \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ，
$∴ \frac{1}{x + 2}$ 是 $\frac{1}{x + 1}$ 的“关联分式”．

(1)、【解决问题】已知分式 $\frac{2}{a^{2} - 1}$ ，则 $\frac{2}{a^{2} + 1}$ $\frac{2}{a^{2} - 1}$ ，的“关联分式”（填“是”或“不是”）．

(2)、和谐小组成员在求分式 $\frac{1}{x^{2} + y^{2}}$ 的“关联分式”时，用了以下方法：
解：设 $\frac{1}{x^{2} + y^{2}}$ 的“关联分式”为B，
则 $\frac{1}{x^{2} + y^{2}} - B = \frac{1}{x^{2} + y^{2}} \times B$ ，
$∴ (\frac{1}{x^{2} + y^{2}} + 1) B = \frac{1}{x^{2} + y^{2}}$ ，
$∴ B = \frac{1}{x^{2} + y^{2} + 1}$ ．
请你仿照和谐小组成员的方法求分式 $\frac{a - b}{2 a + 3 b}$ 的“关联分式”．

(3)、【拓展延伸】观察（1）（2）的结果，寻找规律直接写出分式 $\frac{y}{x}$ 的“关联分式”：．

查看试题解析

北师大版2022-2023学年度第二学期八年级数学 分式的加减法 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期八年级数学分式的加减法期末复习