四川省巴中市2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-05-16 类型:期中考试
一、单选题
-
1. 下列各式中,是一元一次方程的有( )
(1);(2);(3);(4);(5) .A、1个 B、2个 C、3个 D、4个2. 方程的解是( )A、 B、 C、 D、3. 不等式6+3x<0的解集在数轴上表示为( )A、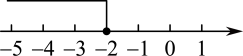 B、
B、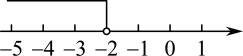 C、
C、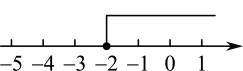 D、
D、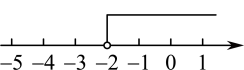 4. 下列方程的变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 去分母得 D、由 , 得5. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、6. 若关于的方程的解是关于的方程的解的2倍,则( )A、 B、 C、 D、-27. 一家商店将某种服饰按成本价提高40%后标价,又以8折(即按标价80%)优惠卖出,结果每件服饰仍可获利15元,则这种服饰的成本价是( )A、125元 B、115元 C、105元 D、95元8. 一元一次不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、9. 已知代数式与是同类项,那么m、n的值分别是( )A、=1,=-2 B、=-1,=-2 C、=1,=2 D、=-2,=110. 方程组的解中,x的值比y的值大1,则k为 ( )A、 B、- C、2 D、-211. 已知关于x的不等式只有两个负整数解,则a的取值范围是( )A、 B、 C、 D、12. 如图是一块在电脑屏幕上出现的长方形色块图,由 6 个不同颜色的正方形组成,已知中间最小的一个正方形的边长为 1,那么这个长方形色块图的周长为( )
4. 下列方程的变形正确的是( )A、由 , 得 B、由 , 得 C、由 , 去分母得 D、由 , 得5. 已知 , 则下列各式中一定成立的是( )A、 B、 C、 D、6. 若关于的方程的解是关于的方程的解的2倍,则( )A、 B、 C、 D、-27. 一家商店将某种服饰按成本价提高40%后标价,又以8折(即按标价80%)优惠卖出,结果每件服饰仍可获利15元,则这种服饰的成本价是( )A、125元 B、115元 C、105元 D、95元8. 一元一次不等式组的解集是 , 则的取值范围是( )A、 B、 C、 D、9. 已知代数式与是同类项,那么m、n的值分别是( )A、=1,=-2 B、=-1,=-2 C、=1,=2 D、=-2,=110. 方程组的解中,x的值比y的值大1,则k为 ( )A、 B、- C、2 D、-211. 已知关于x的不等式只有两个负整数解,则a的取值范围是( )A、 B、 C、 D、12. 如图是一块在电脑屏幕上出现的长方形色块图,由 6 个不同颜色的正方形组成,已知中间最小的一个正方形的边长为 1,那么这个长方形色块图的周长为( )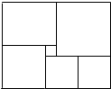 A、42 B、48 C、44 D、50
A、42 B、48 C、44 D、50二、填空题
-
13. 由 ,得到用x表示y的式子为 .14. 已知为关于的一元一次不等式,则15. 不等式的解为 , 则的取值范围是 .16. 把一根长的钢管截成长和长两种规格均有的短钢管,且没有余料,不同的截法有种.17. 若式子的值大于且不大于3,则k的取值范围是 .18. 10个人围成一个圆圈做游戏,游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报3的人心里想的数是 .

三、解答题
-
19. 解下列方程、方程组或不等式组:(1)、(2)、(3)、(4)、解不等式组,并把解集在数轴上表示出来: .
 20. 定义一种新运算“※”: . 例如 , .(1)、计算:的值为;(2)、已知 , 求的值;21. 已知不等式的最小整数解也是关于的方程的解,求此时的值.22. 甲、乙两人各有书若干本,如果甲送乙10本,那么两人所有的书相等;如果乙送给甲10本,那么甲所有的书就是乙剩的书的两倍.问原来甲、乙各有书多少本?23. 如图,点是直线上一点,射线 , , 在直线的上方,射线在直线的下方,且平分 , , .
20. 定义一种新运算“※”: . 例如 , .(1)、计算:的值为;(2)、已知 , 求的值;21. 已知不等式的最小整数解也是关于的方程的解,求此时的值.22. 甲、乙两人各有书若干本,如果甲送乙10本,那么两人所有的书相等;如果乙送给甲10本,那么甲所有的书就是乙剩的书的两倍.问原来甲、乙各有书多少本?23. 如图,点是直线上一点,射线 , , 在直线的上方,射线在直线的下方,且平分 , , .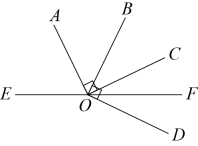 (1)、若 , 求的度数;(2)、若平分 , 求的度数.24. “新冠疫情”对全球经济造成了严重冲击,英雄的武汉人民为抗击“疫情”付出了巨大的努力并取得了伟大的胜利.为了加快复工复产,武汉市某企业需要运输一批生产物资.根据调查得知,2辆大货车与3辆小货车一次可以运输600箱生产物资;5辆大货车与6辆小货车一次可以运输1350箱生产物资.(1)、求1辆大货车和1辆小货车一次分别可以运输多少箱生产物资?(2)、现计划用这样的两种货车共12辆运输这批生产物资,已知每辆大货车一次需要运输费用5000元,每辆小货车一次需要运输费用3000元.若运输物资不少于1500箱,并且运输总费用小于54000元,请你列出所有运输方案,并指出哪种运输方案所需费用最少,最少费用是多少元?25. 如图,A、B两点在一数轴上,其中点O为原点,点A对应的有理数为 , 点B对应的有理数为20.点A以每秒2个单位长度的速度沿数轴向右运动,设运动时间为t秒 .
(1)、若 , 求的度数;(2)、若平分 , 求的度数.24. “新冠疫情”对全球经济造成了严重冲击,英雄的武汉人民为抗击“疫情”付出了巨大的努力并取得了伟大的胜利.为了加快复工复产,武汉市某企业需要运输一批生产物资.根据调查得知,2辆大货车与3辆小货车一次可以运输600箱生产物资;5辆大货车与6辆小货车一次可以运输1350箱生产物资.(1)、求1辆大货车和1辆小货车一次分别可以运输多少箱生产物资?(2)、现计划用这样的两种货车共12辆运输这批生产物资,已知每辆大货车一次需要运输费用5000元,每辆小货车一次需要运输费用3000元.若运输物资不少于1500箱,并且运输总费用小于54000元,请你列出所有运输方案,并指出哪种运输方案所需费用最少,最少费用是多少元?25. 如图,A、B两点在一数轴上,其中点O为原点,点A对应的有理数为 , 点B对应的有理数为20.点A以每秒2个单位长度的速度沿数轴向右运动,设运动时间为t秒 . (1)、当时,点A表示的有理数为 , A、B两点的距离为;(2)、若点B同时以每秒2个单位长度的速度向左运动,经过几秒,点A与点B相遇;(3)、在(2)的条件下,点M(M点在原点)同时以每秒4个单位长度的速度向右运动,几秒后?
(1)、当时,点A表示的有理数为 , A、B两点的距离为;(2)、若点B同时以每秒2个单位长度的速度向左运动,经过几秒,点A与点B相遇;(3)、在(2)的条件下,点M(M点在原点)同时以每秒4个单位长度的速度向右运动,几秒后?