江苏省扬州市广陵区2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-05-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不能由平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{3} + x^{3} = x^{6}$ B、 $(3 x y^{2})^{2} = 6 x^{2} y^{4}$ C、 $2 x^{- 1} = \frac{1}{2 x}$ D、 $x^{7} \div x^{2} = x^{5}$

查看试题解析
3. 下列哪个度数不可能是一个多边形的内角和（）

A、 $360 °$ B、 $600 °$ C、 $900 °$ D、 $1800 °$

查看试题解析
4. 下列说法中正确的是（）

A、三角形的角平分线、中线、高均在三角形内部 B、三角形中至少有一个内角不小于60° C、直角三角形仅有一条高 D、三角形的外角大于任何一个内角

查看试题解析
5. 下列分解因式正确的是（）

A、 $x^{3} - x = x (x^{2} - 1)$ B、 $m^{2} + m + \frac{1}{4} = {(m + \frac{1}{2})}^{2}$ C、 $(a + 4) (a - 4) = a^{2} - 16$ D、 $- x^{2} + y^{2} = (x + y) (x - y)$

查看试题解析
6. 若2和8是一个三角形的两边长，且第三边长为偶数，则该三角形的周长为（）

A、20 B、18 C、17或19 D、18或20

查看试题解析
7. 若m-n=-1，则(m-n)²-2m+2n的值是

A、3 B、2 C、1 D、―1

查看试题解析
8. 如图，大正方形与小正方形的面积之差是30，则阴影部分的面积是（）

A、15 B、10 C、30 D、20

查看试题解析

二、填空题

9. 一粒米的质量是0.000026千克，0.000026用科学记数法表示为．

查看试题解析
10. 一个多边形的内角和比它的外角和的3倍少180°，则这个多边形的边数是.

查看试题解析
11. 已知 $2^{a} \div 4^{b} = 8$ ，则 $a - 2 b$ 的值是．

查看试题解析
12. 如果关于 $x$ 的多项式 $4 x^{2} - (k - 2) x + 9$ 是一个完全平方式，那么 $k =$ ．

查看试题解析
13. 计算 ${(- 0.125)}^{2000} \times 8^{2001} =$ ．

查看试题解析
14. 如图所示，求 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F + ∠ G =$ 度．

查看试题解析
15. 如图，在△ABC中，将∠B、∠C按如图所示的方式折叠，点B、C均落于边BC上的点Q处，MN、EF为折痕，若∠A=82°，则∠MQE=

查看试题解析
16. 若 $(x + 3) (x^{2} - a x + 7)$ 的乘积中不含x的一次项，则 $a =$ ．

查看试题解析
17. 如图，直线m与∠AOB的一边射线OB相交，∠3＝120°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2－∠1＝°．

查看试题解析
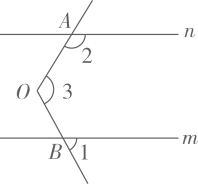18. 如图，在 $△ A B C$ 中，点E是AB边上的点，且 $A E ： E B = 2 ： 3$ ，点D是BC边上的点，且 $B D ： D C = 1 ： 2$ ， AD与CE相交于点F，若四边形BDFE的面积是16，则 $△ A B C$ 的面积为．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 1^{2022} + {(\frac{1}{2})}^{- 2} - {(π - 3)}^{0}$ ；

(2)、 ${(x + 2 y)}^{2} {(x - 2 y)}^{2}$ ．

查看试题解析
20. 分解因式：

(1)、 ${(x + 3)}^{2} - 25$

(2)、 $- x^{3} y + 6 x^{2} y - 9 x y$

查看试题解析
21. 先化简，再求值： ${(x - 2 y)}^{2} - 2 (y - x) (x + y) - y (2 y - 3 x)$ ，其中x，y满足 $| 2 x + 1 | + y^{2} - 2 y + 1 = 0$ ．

查看试题解析
22. 在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC向右平移3格，再向下平移2格，得到△DEF，使点A的对应点为点D，点B的对应点为点E，点C的对应点为点F．

(1)、画出△DEF；

(2)、在图中画出△ABC的AB边上的高线CG（保留利用格点的作图痕迹）；

(3)、△ABC的面积为；

(4)、若AB的长为5，AB边上的高 $C G =$ ．

查看试题解析
23. 已知：如图， $A B // D C$ ，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A.

(1)、求证： $F E // O C$ ；

(2)、若∠BFE=110°，∠A=60°，求∠B的度数.

查看试题解析
24. 已知： $2^{m} = 3 ， 2^{n} = 5$ ．求：

(1)、 $2^{3 m}$ 的值；

(2)、 ${2^{3 m}}^{- 2 n}$ 的值．

查看试题解析
25. 先阅读下列材料，再解答下列问题：
材料：因式分解：（x＋y）²＋2（x＋y）＋1
解：将“x＋y”看成整体，令x＋y＝m，则原式＝m²＋2m＋1＝（m＋1）²
再将x＋y＝m代入，得原式＝（x＋y＋1）²
上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下列问题：

(1)、因式分解：1＋2（x-y）＋（x-y）²＝；

(2)、因式分解：9（x-2）²-6（x-2）＋1

(3)、因式分解：（x²-6x）（x²-6x＋18）＋81

查看试题解析
26. 先阅读下面的内容，再解决问题，
例题：若m²＋2mn＋2n²-6n＋9＝0，求m和n的值．
解：∵m²＋2mn＋2n²-6n＋9＝0
∴m²＋2mn＋n²＋n²-6n＋9＝0
∴（m＋n）²＋（n-3）²＝0
∴m＋n＝0，n-3＝0
∴m＝-3，n＝3

(1)、若x²-2xy＋2y²＋4y＋4＝0，求 $x + y$ 的值．

(2)、已知 $b + 3 a = 2$ ．
①用含 $a$ 的式子表示 $b$ ： ▲ ；

②若 $m^{2} + 8 m = 3 a b - 17$ ，求 ${(a b)}^{m}$ 的值．

查看试题解析
27. 完全平方公式：（a±b）²＝a²±2ab＋b²适当的变形，可以解决很多的数学问题．
例如：若a＋b＝3，ab＝1，求a²＋b²的值．
解：因为a＋b＝3，ab＝1，所以（a＋b）²＝9，2ab＝2
所以a²＋b²＋2ab＝9；得a²＋b²＝7
根据上面的解题思路与方法，解决下列问题：

(1)、若x＋y＝6，x²＋y²＝30，求xy的值；

(2)、请直接写出下列问题答案：
①若3a＋b＝7，ab＝2，则 $3 a - b$ ＝；
②若（3-x）（5-x）＝8，则（3-x）²＋（5-x）²＝．

(3)、如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝10，两正方形的面积和S₁＋S₂＝76，求图中阴影部分面积．

查看试题解析
28. 【概念认识】
如图①，在 $∠ A B C$ 中，若 $∠ A B D = ∠ D B E = ∠ E B C$ ，则 $B D$ ， $B E$ 叫做 $∠ A B C$ 的“三分线”．其中， $B D$ 是“邻 $A B$ 三分线”， $B E$ 是“邻 $B C$ 三分线”．

【问题解决】

(1)、如图②，在 $△ A B C$ 中， $∠ A = 80 ° ， ∠ B = 45 °$ ，若 $∠ B$ 的三分线 $B D$ 交 $A C$ 于点D，求 $∠ B D C$ 的度数；

(2)、如图③，在 $△ A B C$ 中， $B P 、 C P$ 分别是 $∠ A B C$ 邻 $B C$ 三分线和 $∠ A C B$ 邻 $B C$ 三分线，且 $∠ B P C = 140 °$ ，求 $∠ A$ 的度数；

(3)、【延伸推广】在 $△ A B C$ 中， $∠ A C D$ 是 $△ A B C$ 的外角， $∠ B$ 的三分线所在的直线与 $∠ A C D$ 的三分线所在的直线交于点P．若 $∠ A = m °$ （ $m > 54$ ）， $∠ B = 54 °$ ，直接写出 $∠ B P C$ 的度数．（用含m的代数式表示）

查看试题解析