江苏省无锡市江阴市2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-16 类型:期中考试
一、单选题
-
1. 习近平总书记强调,“垃圾分类工作就是新时尚”.下列垃圾分类标识的图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知分式 的值是零,那么x的值是( )A、﹣1 B、0 C、1 D、±13. 下列事件为确定事件的是( )A、6张相同的小标签分别标有数字1~6,从中任意抽取一张,抽到3号签 B、长度分别是4,6,8的三条线段能围成一个三角形 C、射击运动员射击一次,命中靶心 D、抛掷1枚质地均匀的硬币反面朝上4. 某校八年级有452名学生,为了了解这452名学生的课外阅读情况,从中抽取50名学生进行统计.在这个问题中,样本是( )A、452名学生 B、抽取的50名学生 C、452名学生的课外阅读情况 D、抽取的50名学生的课外阅读情况5. 菱形具有而矩形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、邻边互相垂直 D、对角线互相垂直6. 如果把分式 中的 和 都同时扩大2倍,那么分式的值( )A、不变 B、扩大4倍 C、缩小2倍 D、扩大2倍7. 下列分式中,属于最简分式的是( )A、 B、 C、 D、8. 如图,在中,∠A=70°, , 以点B为旋转中心把按顺时针旋转一定角度,得到 , 点恰好落在上,连接 , 则度数为( )
2. 已知分式 的值是零,那么x的值是( )A、﹣1 B、0 C、1 D、±13. 下列事件为确定事件的是( )A、6张相同的小标签分别标有数字1~6,从中任意抽取一张,抽到3号签 B、长度分别是4,6,8的三条线段能围成一个三角形 C、射击运动员射击一次,命中靶心 D、抛掷1枚质地均匀的硬币反面朝上4. 某校八年级有452名学生,为了了解这452名学生的课外阅读情况,从中抽取50名学生进行统计.在这个问题中,样本是( )A、452名学生 B、抽取的50名学生 C、452名学生的课外阅读情况 D、抽取的50名学生的课外阅读情况5. 菱形具有而矩形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、邻边互相垂直 D、对角线互相垂直6. 如果把分式 中的 和 都同时扩大2倍,那么分式的值( )A、不变 B、扩大4倍 C、缩小2倍 D、扩大2倍7. 下列分式中,属于最简分式的是( )A、 B、 C、 D、8. 如图,在中,∠A=70°, , 以点B为旋转中心把按顺时针旋转一定角度,得到 , 点恰好落在上,连接 , 则度数为( ) A、 B、 C、 D、9. 如图,在边长为5的正方形中,点M为线段上一点,且 , 点P是对角线上一动点,过点P作于点E,于点F,则的最小值为( )
A、 B、 C、 D、9. 如图,在边长为5的正方形中,点M为线段上一点,且 , 点P是对角线上一动点,过点P作于点E,于点F,则的最小值为( ) A、 B、 C、 D、10. 如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的( )
A、 B、 C、 D、10. 如图,一个瓶身为圆柱体的玻璃瓶内装有高a厘米的墨水,将瓶盖盖好后倒置,墨水水面高为h厘米,则瓶内的墨水的体积约占玻璃瓶容积的( )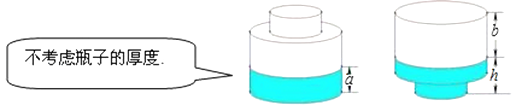 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的最简公分母是 .12. 20230418中数字“2”出现的频率是 .13. 已知平行四边形ABCD中, , 则度.14. 已知关于x的分式方程的解是非负数,则m的取值范围是 .15. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.
 16. 如图,在边长为10的菱形中,对角线 , 则菱形的面积是 , 若点O是线段上的动点,于E,于F.则 .
16. 如图,在边长为10的菱形中,对角线 , 则菱形的面积是 , 若点O是线段上的动点,于E,于F.则 . 17. 如图①,将四边形纸片沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如图②所示的平行四边形,若要密铺后的平行四边形为矩形,则四边形需要满足的条件是 .
17. 如图①,将四边形纸片沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如图②所示的平行四边形,若要密铺后的平行四边形为矩形,则四边形需要满足的条件是 . 18. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .
18. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .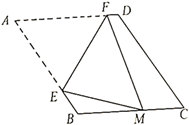
三、解答题
-
19. 计算:(1)、(2)、 .20. 解方式方程(1)、;(2)、;21. 先化简 ,然后a在﹣1,1,2三个数中任选一个合适的数代入求值.22. 微信圈有篇热传的文章《如果想毁掉一个孩子,就给他一部手机!》.国际上,法国教育部宣布,小学和初中于2018年9月新学期开始,禁止学生使用手机,为了解学生手机使用情况.高新区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,图②的统计图.已知“查资料”的人数是40人.
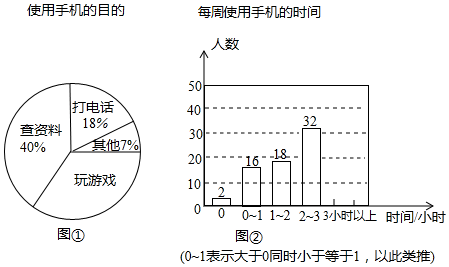 (1)、在这次调查中,一共抽取了 名学生;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是 度;(3)、补全条形统计图;(4)、该校共有学生2000人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.23. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知 , . C是第四象限内的一个格点,由点C与线段组成一个以为底,且腰长为无理数的等腰三角形.
(1)、在这次调查中,一共抽取了 名学生;(2)、在扇形统计图中,“玩游戏”对应的圆心角的度数是 度;(3)、补全条形统计图;(4)、该校共有学生2000人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.23. 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知 , . C是第四象限内的一个格点,由点C与线段组成一个以为底,且腰长为无理数的等腰三角形. (1)、填空:C点的坐标是 , 的面积是 ;(2)、将绕点C旋转180°得到 , 连接、 , 则四边形的形状是何特殊四边形?(3)、请探究:在y轴上是否存在这样的点P,使四边形的面积等于面积的2.5倍?若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.24. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.
(1)、填空:C点的坐标是 , 的面积是 ;(2)、将绕点C旋转180°得到 , 连接、 , 则四边形的形状是何特殊四边形?(3)、请探究:在y轴上是否存在这样的点P,使四边形的面积等于面积的2.5倍?若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.24. 如图,在平行四边形中,过点作于点点在边上,连接AF,BF.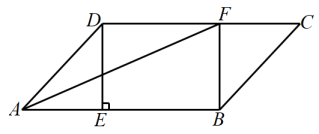 (1)、求证:四边形是矩形;(2)、若平分求四边形的面积.25. 某汽车网站对两款售价相同,续航里程相同的汽车做了一次评测,一款为燃油车,另一款为纯电新能源车.得到相关数据如下:
(1)、求证:四边形是矩形;(2)、若平分求四边形的面积.25. 某汽车网站对两款售价相同,续航里程相同的汽车做了一次评测,一款为燃油车,另一款为纯电新能源车.得到相关数据如下:燃油车
纯电新能源车
油箱容积:48升
电池容量:90千瓦时
油价:8元/升
电价:0.6元/千瓦时
续航里程:a千米
续航里程:a千米
每千米行驶费用:元
每千米行驶费用:____元
(1)、用含a的代数式表示新能源车的每千米行驶费用元(结果为最简);(2)、若燃油车每千米行驶费用比纯电新能源车多0.55元.①请分别求出这两款车的每千米行驶费用;
②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元.问:每年行驶里程超过多少千米时,新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
26. 如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为xcm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).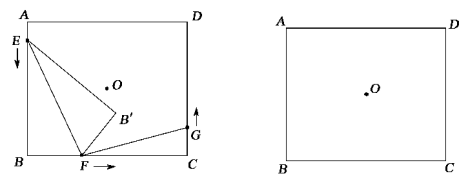 (1)、当t=s时,四边形EBFB'为正方形;(2)、当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?(3)、是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
(1)、当t=s时,四边形EBFB'为正方形;(2)、当x为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形可能全等?(3)、是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.