北师大版2022-2023学年度第二学期八年级数学 简单的图案设计 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,在 的正方形网格中两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有( )
 A、4种 B、5种 C、6种 D、7种2. 下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A、
A、4种 B、5种 C、6种 D、7种2. 下面四个图案中,不能由基本图案(图中阴影部分)旋转得到的是( )A、 B、
B、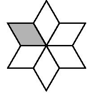 C、
C、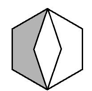 D、
D、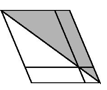 3. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
3. 如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )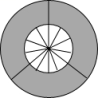 A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的4. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A、平移一次形成的 B、平移两次形成的 C、以轴心为旋转中心,旋转后形成的 D、以轴心为旋转中心,旋转、后形成的4. 在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是( )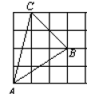 A、
A、 B、
B、 C、
C、 D、
D、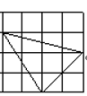 5. 由基本图案1得到图案2的方法是 ( )
5. 由基本图案1得到图案2的方法是 ( )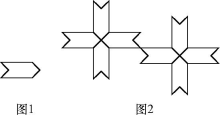 A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称6. 如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( )
A、旋转和平移 B、中心对称和轴对称 C、平移和轴对称 D、中心对称6. 如图所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的一个是( ) A、A B、B C、C D、D7. 下列图案中,可以由一个”基本图案”连续旋转45°得到的是( )
A、A B、B C、C D、D7. 下列图案中,可以由一个”基本图案”连续旋转45°得到的是( )
A、 B、
B、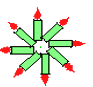 C、
C、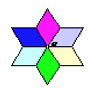 D、
D、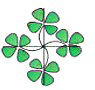 8. 如图中的四个图案,四位同学分别说出了它们的形成过程,其中说得不正确的是( )
8. 如图中的四个图案,四位同学分别说出了它们的形成过程,其中说得不正确的是( )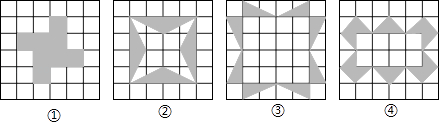 A、图①是一个长方形绕着图形的中心按逆时针旋转90°,180°和270°所得 B、图②可由一个钝角三角形绕着图形的中心按同一方向旋转90°,180°和270°形成 C、图③可以看作以正方形的一条对角线所在直线为对称轴翻折所得 D、图④可以看作由长方形的一边的垂直平分线为对称轴翻折而成9. 如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )
A、图①是一个长方形绕着图形的中心按逆时针旋转90°,180°和270°所得 B、图②可由一个钝角三角形绕着图形的中心按同一方向旋转90°,180°和270°形成 C、图③可以看作以正方形的一条对角线所在直线为对称轴翻折所得 D、图④可以看作由长方形的一边的垂直平分线为对称轴翻折而成9. 如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( ) A、5 B、6 C、4 D、710. 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A、5 B、6 C、4 D、710. 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( ) A、2种 B、3种 C、4种 D、5种
A、2种 B、3种 C、4种 D、5种二、填空题
-
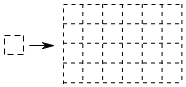
11. 有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作次.
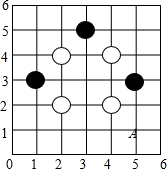
 12. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)
12. 如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序实数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(请填写正确答案的序号)①黑(1,5),白(5,5);②黑(3,2),白(3,3);③黑(3,3),白(3,1);④黑(3,1),白(3,3)
 13. 如图: 为五个等圆的圆心,且 在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是.
13. 如图: 为五个等圆的圆心,且 在一条直线上,请在图中画一条直线,将这五个圆分成面积相等的两个部分,并说明这条直线经过的两点是.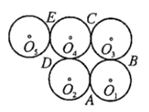 14. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.
14. 把18个边长都为1的等边三角形如图拼接成平行四边形,且其中6个涂上了阴影,现在,可以旋转、翻折或平移某一个阴影等边三角形到某一个空白的等边三角形处,使新构成的阴影部分图案是轴对称图形,共可得种轴对称图形.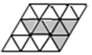 15. 如图,在平面直角坐标系xOy中,△ABC经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:.
15. 如图,在平面直角坐标系xOy中,△ABC经过若干次图形的变化(平移、轴对称、旋转)得到△DEF,写出一种由△ABC得到△DEF的过程:.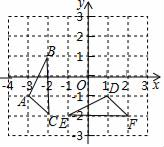
三、解答题
-
16. 利用1个等腰三角形、2个长方形、3个圆,可以构造出许多独特且有意义的轴对称图形,如图已给出四幅图,你能再构思出一些轴对称图形吗(画出3个即可)?别忘了加一两句贴切、有创意的解说词.
 17. 观察下列图案(如图),分别指出每个图案是由哪个“基本图案”旋转得来的.
17. 观察下列图案(如图),分别指出每个图案是由哪个“基本图案”旋转得来的.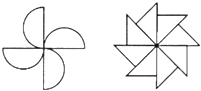 18. 在5×7的方格纸上,任意选出5个小方块涂上颜色,使整个图形(包括着色的“对称”)有:
18. 在5×7的方格纸上,任意选出5个小方块涂上颜色,使整个图形(包括着色的“对称”)有:
①1条对称轴;
②2条对称轴;
③4条对称轴.
四、综合题
-
19. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.
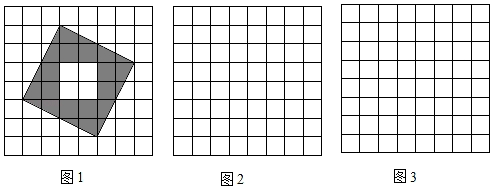 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
20.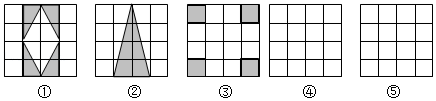 (1)、观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征:; ;(2)、在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.21. 如图都是由边长为1的小等边三角形构成的网格图,每个网格图中有3个小等边三角形已涂上阴影.
(1)、观察图①~图③中阴影部分的图形,写出这3个图形具有的两个共同特征:; ;(2)、在图④、图⑤中设计一个新的图形,使它也具有这两个共同特征.21. 如图都是由边长为1的小等边三角形构成的网格图,每个网格图中有3个小等边三角形已涂上阴影. (1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).22. 如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.
(1)、请在下面①②③三个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个轴对称图形(3个图形中所涂三角形不同);(2)、在④⑤两个网格图中分别涂上一个三角形,使得4个阴影小等边三角形组成一个中心对称图形(2个图形中所涂三角形不同).22. 如图,在6×6的方格中,点A,O,B都在小方格的顶点上,请在方格中取点C和D,画△AOC和△BOD,使这两个三角形全等.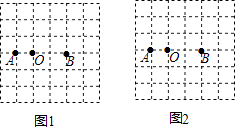 (1)、在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.(2)、在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.23. 在一块长16m.宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
(1)、在图1中画出的两个三角形,可以使其中一个三角形通过轴对称得到另一个三角形.(2)、在图2中画出的两个三角形,可以使其中一个三角形通过旋转得到另一个三角形.23. 在一块长16m.宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.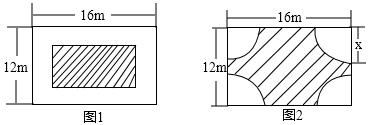

小明说:我的设计方案如图(1),其中花园四周小路的宽度相等. 通过解方程,我得到小路的宽为2m或12m.
小颖说:我的设计方案如图(2),其中花园中每个角上的扇形相同.
(1)、你认为小明的结果对吗?请说明理由.(2)、请你帮助小颖求出图中的x(精确到0.1m).(3)、你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.