北师大版2022-2023学年度第二学期八年级数学 图形的旋转 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,将绕点按逆时针方向旋转 , 得到.若点恰好在线段BC的延长线上,且 , 则旋转角的度数为( )
 A、60° B、70° C、100° D、110°2. 如图,将绕点A逆时针旋转得到.若点D在线段的延长线上,则的大小为( )
A、60° B、70° C、100° D、110°2. 如图,将绕点A逆时针旋转得到.若点D在线段的延长线上,则的大小为( ) A、 B、 C、 D、3. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、 B、 C、 D、3. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( ) A、①② B、②③ C、①③ D、①②③4. 如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBG.延长AE交CG于点F,连接DE.下列结论:①AF⊥CG,②四边形BEFG是正方形,③若DA=DE,则CF=FG;其中正确的结论是( )
A、①② B、②③ C、①③ D、①②③4. 如图,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBG.延长AE交CG于点F,连接DE.下列结论:①AF⊥CG,②四边形BEFG是正方形,③若DA=DE,则CF=FG;其中正确的结论是( ) A、①②③ B、①② C、②③ D、①③5. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )
A、①②③ B、①② C、②③ D、①③5. 如图,在正方形中,将边绕点B逆时针旋转至 , 连接 , , 若 , , 则线段的长度为( )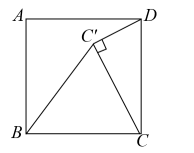 A、 B、 C、 D、36. 如图,将△AOB绕点O按逆时针方向旋转60°后得到 , 若∠AOB=25°,则的度数是( )
A、 B、 C、 D、36. 如图,将△AOB绕点O按逆时针方向旋转60°后得到 , 若∠AOB=25°,则的度数是( ) A、25° B、35° C、40° D、85°7. 如图,中, , 将绕点C顺时针旋转,得到 , 点A的对应点D在的延长线上,则旋转角为( )
A、25° B、35° C、40° D、85°7. 如图,中, , 将绕点C顺时针旋转,得到 , 点A的对应点D在的延长线上,则旋转角为( ) A、 B、 C、 D、8. 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC,若AB=10,BC=6.则线段BE的长为( )
A、 B、 C、 D、8. 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC,若AB=10,BC=6.则线段BE的长为( ) A、10 B、12 C、14 D、169. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO;⑤S△AOC+S△AOB= . 其中正确的结论是( )
A、10 B、12 C、14 D、169. 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO;⑤S△AOC+S△AOB= . 其中正确的结论是( )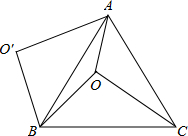 A、①②③⑤ B、①②③④ C、①②③④⑤ D、①②③10. 如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为( )
A、①②③⑤ B、①②③④ C、①②③④⑤ D、①②③10. 如图,将△ABC绕点A逆时针旋转55°,得到△ADE,若∠E=65°,且AD⊥BC于点F,则∠BAC的度数为( ) A、65° B、70° C、75° D、80°
A、65° B、70° C、75° D、80°二、填空题
-
11. 如图,中, , , , P为线段上一动点,连接 , 绕点B顺时针旋转到 , 连接.设 , , y与x的函数关系式是.
 12. 如图,在△ABC中,∠C=60°,AC=6,BC=11,将△ABC绕点A沿顺时针方向旋转,当点C的对应点落在BC边上时停止,则此时的长为.
12. 如图,在△ABC中,∠C=60°,AC=6,BC=11,将△ABC绕点A沿顺时针方向旋转,当点C的对应点落在BC边上时停止,则此时的长为.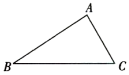 13. 如图,等边三角形ABC内有一点P,分别连接AP,BP,CP,若AP=6,BP=8,CP=10,则S△ABP+S△BPC=.
13. 如图,等边三角形ABC内有一点P,分别连接AP,BP,CP,若AP=6,BP=8,CP=10,则S△ABP+S△BPC=.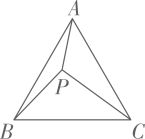 14. 如图,在△ABC中,AB=10,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为 .
14. 如图,在△ABC中,AB=10,将△ABC绕点B按逆时针方向旋转30°后得到△A1BC1 , 则阴影部分的面积为 .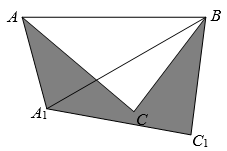 15. 在如图正方形网格中,绕某点旋转一定的角度得到 , 则其旋转中心是.
15. 在如图正方形网格中,绕某点旋转一定的角度得到 , 则其旋转中心是.
三、解答题
-
16. 如图,在中, , 在同一平面内,将绕点逆时针旋转到的位置,连接 , 求证:.
 17. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
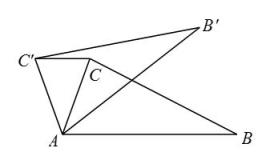
17. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长. 18. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心.
18. 如图,逆时针旋转一定角度后与重合,且点在上.若 , , 求出旋转角的度数,并写出旋转中心.
四、综合题
-
19. 在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放,其中 , , .
 (1)、;(2)、小昕同学将三角板绕点按顺时针方向旋转.
(1)、;(2)、小昕同学将三角板绕点按顺时针方向旋转.(i)如图2,当点落在边上时,延长交于点 , 求的长.
(ii)若点、、在同一条直线上,请画出示意图并求点到直线的距离.
20. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).( 1 )请按下列要求画图:

①平移△ABC,使点A的对应点A1的坐标为(-4,-3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2 .
( 2 )若将△A1B1C1绕点M旋转可得到△A2B2C2 , 请直接写出旋转中心M点的坐标 .
21. 如图1,在平面直角坐标系中,△ABO为直角三角形,∠ABO=90°,∠AOB=30°,OB=3,点C为OB上一动点. (1)、点A的坐标为;(2)、连接AC,并延长交y轴于点D,若△OAD的面积恰好被x轴分成1∶2两部分,求点C的坐标;(3)、如图2,若∠OAC=30°,将△OAB绕点O顺时针旋转,得到△OA'B',如图2所示,OA'所在直线交直线AC于点P,当△OAP为直角三角形时,直接写出点的坐标.22. 在平面直角坐标系中的位置如图所示.
(1)、点A的坐标为;(2)、连接AC,并延长交y轴于点D,若△OAD的面积恰好被x轴分成1∶2两部分,求点C的坐标;(3)、如图2,若∠OAC=30°,将△OAB绕点O顺时针旋转,得到△OA'B',如图2所示,OA'所在直线交直线AC于点P,当△OAP为直角三角形时,直接写出点的坐标.22. 在平面直角坐标系中的位置如图所示. (1)、将先向下平移4个单位,再向左平移1个单位得到 , 请写出移动后的点坐标 , 坐标 .(2)、将绕着点顺时针方向旋转得到 , 画出 .23. 通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
(1)、将先向下平移4个单位,再向左平移1个单位得到 , 请写出移动后的点坐标 , 坐标 .(2)、将绕着点顺时针方向旋转得到 , 画出 .23. 通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
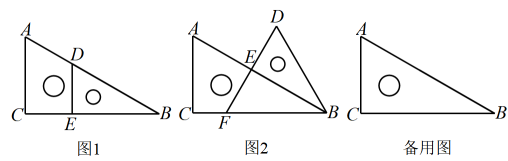
原题:如图1,点E、F分别在正方形的边、上, , 连接 , 试猜想、、之间的数量关系.
(1)、思路梳理把绕点A逆时针旋转90°至 , 可使与重合,由 , 得 , 即点F、D、G共线,易证 , 故、、之间的数量关系为 . (要求写出必要的推理过程)
(2)、类比引申如图2,点E、F分别在正方形的边、的延长线上, , 连接 , 试猜想、、之间的数量关系为 , 并给出证明.
(3)、联想拓展如图3,在中, , , 点D、E均在边上,且 , 若 , , 求的长.