北师大版2022-2023学年度第二学期八年级数学 图形的平移 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图, , 将直角三角形沿着射线方向平移 , 得三角形已知 , 则阴影部分的周长为( )
 A、 B、 C、 D、2. 如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )
A、 B、 C、 D、2. 如图,三角形ABC沿着BC所在直线向右平移a个单位长度得到三角形DEF(点E在点C的左侧).下列判断正确的是( )结论Ⅰ:若BF=8,EC=4,则a的值为2;
结论Ⅱ:连接AD,若三角形ABC的周长为18,四边形ABFD的周长为22,则a的值为4.
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对3. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或4. 如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对3. 在平面直角坐标系中,将点P (−x,1−x)先向右平移3个单位得点P1 , 再将P1向下平移3个单位得点P2 , 若点P2落在第四象限,则x的取值范围是( )A、 B、 C、 D、或4. 如图,在平面直角坐标系中,等边△OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( ) A、(4,2) B、(3,3) C、(4,3) D、(3,2)5. 以图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
A、(4,2) B、(3,3) C、(4,3) D、(3,2)5. 以图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
 A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°,再向右平移1个单位 C、先以直线AB为对称轴进行翻折,再向右平移1个单位 D、只要向右平移1个单位6. 在平面直角坐标系中,线段AB的两个端点分别是 , , 将线段AB平移后,得到线段 , 点的坐标为 , 则点的坐标为( )A、 B、 C、 D、7. 将直线向下平移1个单位长度后的直线解析式为( )A、 B、 C、 D、8. “冰墩墩”将熊猫形象与富有超能量的冰晶外壳结合,体现了冬季冰雪运动与现代科技的特点.将如图所示的“冰墩墩”图案平移后可以得到( )
A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°,再向右平移1个单位 C、先以直线AB为对称轴进行翻折,再向右平移1个单位 D、只要向右平移1个单位6. 在平面直角坐标系中,线段AB的两个端点分别是 , , 将线段AB平移后,得到线段 , 点的坐标为 , 则点的坐标为( )A、 B、 C、 D、7. 将直线向下平移1个单位长度后的直线解析式为( )A、 B、 C、 D、8. “冰墩墩”将熊猫形象与富有超能量的冰晶外壳结合,体现了冬季冰雪运动与现代科技的特点.将如图所示的“冰墩墩”图案平移后可以得到( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 将函数的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )A、 B、 C、 D、10. 如图矩形的边在轴的正半轴上,点的坐标为 , 且= . 将直线沿轴方向平移,若直线与矩形的边有公共点,则的取值范围是( )
9. 将函数的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )A、 B、 C、 D、10. 如图矩形的边在轴的正半轴上,点的坐标为 , 且= . 将直线沿轴方向平移,若直线与矩形的边有公共点,则的取值范围是( )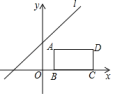 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , , , 将沿射线方向平移2个单位后得到 , 连接 , 则的长为.
 12. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要元.
12. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要元. 13. 已知点Q的坐标为(-1,3),若将点Q向上平移1个单位长度,再向右平移5个单位长度,得到点P,则点P的坐标是.14. 如图,把沿方向平移得到 , 则的长是.
13. 已知点Q的坐标为(-1,3),若将点Q向上平移1个单位长度,再向右平移5个单位长度,得到点P,则点P的坐标是.14. 如图,把沿方向平移得到 , 则的长是. 15. 在平面直角坐标系中,点M(-4,1),先向右平移2个单位,再作关于y轴对称,最后得到的点的坐标为 .
15. 在平面直角坐标系中,点M(-4,1),先向右平移2个单位,再作关于y轴对称,最后得到的点的坐标为 .三、解答题
-
16. 如图,△ABC是等边三角形,将线段AC绕点C顺时针旋转40°,得到线段CD,连接BD,求∠ABD的度数.
 17. 如图: , , 若将线段平移至 , 求a与b的值.
17. 如图: , , 若将线段平移至 , 求a与b的值. 18. 如图,在中, , 线段绕点按逆时针方向旋转得到线段 , 由沿方向平移得到的,且直线恰好过点 . 求证: .
18. 如图,在中, , 线段绕点按逆时针方向旋转得到线段 , 由沿方向平移得到的,且直线恰好过点 . 求证: .
四、综合题
-
19. 中,AD平分.
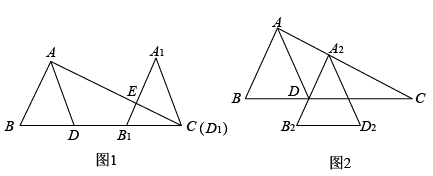 (1)、如图1,将沿BC方向平移,得 , 使得点与点C重合,交AC于点E.求证:;(2)、如图2,将沿着AC方向平移,得到 , 使得经过点D,求证:平分.20. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).
(1)、如图1,将沿BC方向平移,得 , 使得点与点C重合,交AC于点E.求证:;(2)、如图2,将沿着AC方向平移,得到 , 使得经过点D,求证:平分.20. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3),B(-3,1),C(-1,3).( 1 )请按下列要求画图:

①平移△ABC,使点A的对应点A1的坐标为(-4,-3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2 .
( 2 )若将△A1B1C1绕点M旋转可得到△A2B2C2 , 请直接写出旋转中心M点的坐标 .
21. 如图,在直角坐标系中,已知点O,A的坐标分别为 , . (1)、点B的坐标是 , 点B与点A之间的距离是 . 将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整数点,在四边形内部(不包括边界)的整数点M使 , 请直接写出所有点M的可能坐标.
(1)、点B的坐标是 , 点B与点A之间的距离是 . 将点B,点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整数点,在四边形内部(不包括边界)的整数点M使 , 请直接写出所有点M的可能坐标.

