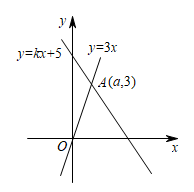北师大版2022-2023学年度第二学期八年级数学 一元一次不等式与一元函数 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,一次函数与一次函数的图象交于点P(1,3),则关于x的不等式的解集是( )
 A、x≥1 B、x>1 C、x>0 D、x<12. 如图,直线y=x+m与y=nx-5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx-5n>0的整数解为( )
A、x≥1 B、x>1 C、x>0 D、x<12. 如图,直线y=x+m与y=nx-5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx-5n>0的整数解为( )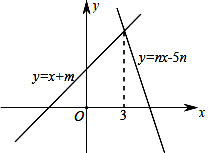 A、6 B、5 C、4 D、33. 一次函数的图象如图所示,则下列结论正确的是( )
A、6 B、5 C、4 D、33. 一次函数的图象如图所示,则下列结论正确的是( ) A、当时, B、当时, C、当时, D、当时,4. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )
A、当时, B、当时, C、当时, D、当时,4. 如图,在同一平面直角坐标系中,一次函数的图象与正比例函数的图象相交于点A,且点A的纵坐标是2,则不等式的解集是( )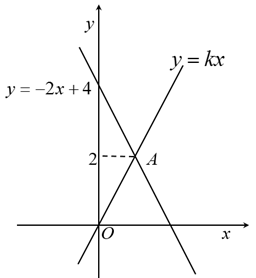 A、 B、 C、 D、5. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
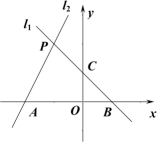
A、 B、 C、 D、5. 我们知道,若ab>0.则有或 . 如图,直线y=kx+b与y=mx+n分别交x轴于点A(-0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( ) A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>26. 如图,直线过点A、B,则不等式的解集是( )
A、x>2 B、-0.5<x<2 C、0<x<2 D、x<-0.5或x>26. 如图,直线过点A、B,则不等式的解集是( ) A、 B、 C、 D、7. 如图是函数的图象.已知函数的图象与的图象交于A、B两点,且 , 则满足的x的取值范围是( )
A、 B、 C、 D、7. 如图是函数的图象.已知函数的图象与的图象交于A、B两点,且 , 则满足的x的取值范围是( )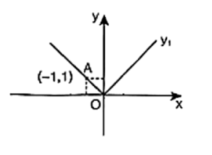 A、或 B、或 C、 D、8. 如图,直线与直线相交于点 , 则关于x的不等式的解为( )
A、或 B、或 C、 D、8. 如图,直线与直线相交于点 , 则关于x的不等式的解为( ) A、 B、 C、 D、9. 直线: 与直线:在同一平面直角坐标系的图象如图所示,则关于的不等式的解集为( )
A、 B、 C、 D、9. 直线: 与直线:在同一平面直角坐标系的图象如图所示,则关于的不等式的解集为( ) A、 B、 C、 D、10. 如图,直线:与直线:相交于点 , 则关于的不等式的解集是( )
A、 B、 C、 D、10. 如图,直线:与直线:相交于点 , 则关于的不等式的解集是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,一次函数的图象经过点 , 则关于x的不等式的解集为 .
 12. 如图,直线与轴、轴的交点分别为 , , 则关于的不等式的解集为.
12. 如图,直线与轴、轴的交点分别为 , , 则关于的不等式的解集为. 13. 如图,直线与直线相交于点 , 则关于x的不等式的解集是.
13. 如图,直线与直线相交于点 , 则关于x的不等式的解集是. 14. 如图所示,直线经过点 , 则关于x的不等式的解集为.
14. 如图所示,直线经过点 , 则关于x的不等式的解集为.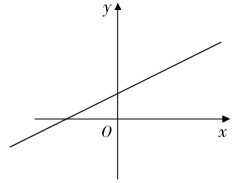 15. 如图,一次函数与x轴、y轴分别交于A、B两点,则不等式的解集是 .
15. 如图,一次函数与x轴、y轴分别交于A、B两点,则不等式的解集是 .
三、解答题
-
16. 由于灯管老化,现某学校要购进A、B两种节能灯管320只,A、B两种灯管的单价分别为25元和30元,现要求B种灯管的数量不少于A种灯管的3倍,那么购买A种灯管多少只时,可使所付金额最少?最少为多少元?17. 直线 过点 ,直线 过点 ,求不等式 的解集.18. 已知一次函数 ,当 时, ,求此一次函数的表达式.
四、综合题
-
19. 某村在政府的扶持下建起了鲜花大棚基地,准备种植 , 两种鲜花。经测算,种植两种鲜花每亩的投入与获利情况如下表:
每亩需投入(万元)
每亩可获利(万元)
种鲜花
2
0.8
种鲜花
4
1.2
(1)、政府和村共同投入200万元全部用来种植这两种鲜花,总获利万元.设种植种鲜花亩,求关于的函数关系式;(2)、在(1)的条件下,若要求A种鲜花的种植面积不能多于B种鲜花种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.20. 已知一次函数的图像与轴的交点在轴的上方,且随 的增大而减小.(1)、求整数的值;(2)、在(1)的结论下,在下面的平面直角坐标系中画出函数的图象,并根据图像回答:当取何值时,? ? ?