北师大版2022-2023学年度第二学期八年级数学一元一次不等式期末复习

试卷更新日期：2023-05-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知方程 $\frac{3 - a}{a - 4} - a = \frac{1}{4 - a}$ ，且关于x的不等式 $a < x \leq b$ 只有2个整数解，那么b的取值范围是（）

A、 $1 < b \leq 2$ B、 $2 < b \leq 3$ C、 $1 \leq b < 2$ D、 $2 \leq b < 3$

查看试题解析
2. 关于x的一元一次不等式x-3＜0的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
3. 不等式 $\frac{5 x + 3}{2} \leq 3 x$ 的解集是（）

A、 $x \leq - 3$ B、 $x \geq - 3$ C、 $x \leq 3$ D、 $x ≥ 3$

查看试题解析
4. 下列变形中正确的是（）

A、由 $- 2 x < 1$ ，得 $x < - \frac{1}{2}$ B、由 $2 x + 1 > 3 x - 1$ ，得 $x > - 2$ C、由 $2 x + 1 > x - 1$ ，得 $x > 2$ D、由 $x + 2 < 2 x - 2$ ，得 $x > 4$

查看试题解析
5. 关于x的不等式： $x < 2 x - a$ 有3个负整数解，则a的取值范围是（）

A、 $- 4 \leq a < - 3$ B、 $- 5 \leq a < - 4$ C、 $- 4 < a \leq - 3$ D、 $- 5 < a \leq - 4$

查看试题解析
6. 下列语句中，正确的是（）

A、小朋还不到十五岁，设小明 $x$ 岁，则有 $x \leq 15$ B、甲数 $a$ 的三倍比乙数 $b$ 大4个单位，则有 $3 a > b + 4$ C、某数 $M$ 是非负数，则有 $M < 0$ D、卡车载重限重5吨，设卡车载重y吨，则有 $y \leq 5$

查看试题解析
7. 为解决部分家长在放学时间不能按时接孩子的问题，我市许多学校都启动了“课后服务”工作．某学校为了开展好课后服务，计划用不超过10000元的资金购买足球、篮球和排球用于球类兴趣班，已知足球、篮球、排球的单价分别为100元、80元、60元，且根据参加球类兴趣班的学生数了解到以下信息：①篮球的数量必须比足球多10个，②排球的数量必须是足球的3倍．则学校最多能购买足球的个数是（）

A、10 B、25 C、26 D、30

查看试题解析
8. 若 $(a - 2) x^{| a - 1 |} - 2 < 0$ 是关于 $x$ 的一元一次不等式.则 $a$ 的值为（）

A、2 B、-1 C、0 D、0或2

查看试题解析
9. 已知三个连续正整数的和小于15，则这样的数共有（）组．

A、6 B、5 C、4 D、3

查看试题解析
10. 一次学校智力竞赛中共有 $20$ 道题，规定答对一题得 $5$ 分，答错或不答一道题扣 $2$ 分，得分为 $75$ 分以上可以获得奖品，小锋在本次竞赛中获得了奖品．假设小锋答对了 $x$ 题，可根据题意列出不等式（）

A、 $5 x + 2 (20 - x) \geq 75$ B、 $5 x + 2 (20 - x) > 75$ C、 $5 x - 2 (20 - x) > 75$ D、 $5 x - 2 (20 - x) \geq 75$

查看试题解析

二、填空题

11. 写出一个解为 $x ≥ 1$ 且一次项系数大于3的一元一次不等式.

查看试题解析
12. 不等式 $3 x + 2 \geq 5 x - 8$ 的解为.

查看试题解析
13. 若一次函数y＝kx＋b的图像如图所示，则关于kx＋ $\frac{3}{2}$ b＞0的不等式的解集为.

查看试题解析
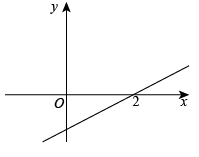14. 已知关于x的一元二次方程 $x^{2} + 2 x + 1 + m = 0$ 有两个不相等的实数根，则实数m的取值范围是．

查看试题解析
15. 若(2a-1)x<2a-1的解集是x>1 ，则a 的取值范围是.

查看试题解析

三、解答题

16. 对于不等式 $\frac{2 x - 1}{3} \leq 1 - \frac{x + 1}{2}$ ，圆圆的解法如下：
解：原不等式可化为 $2 (2 x - 1) \leq 1 - 3 (x + 1)$
去括号得 $4 x - 2 \leq 1 - 3 x - 3$
合并同类项得 $7 x \leq 0$
所以原不等式的解为 $x \leq 0$
圆圆的解法是否正确？如果不正确，请提供正确的解法.

查看试题解析
17. 一次数学竞赛中，共有20道题，规定答对一道题得6分，答错或不答一道题扣2分；80分以上（含80分）可以获奖，问若要获奖，至少要答对几道题？

查看试题解析
18. 在元旦前夕，某商场为儿童推出一款特价商品，某超市为了促销这种定价为4元/件的商品，采取下列方式优惠销售：若一次性购买不超过3件，按原价付款；若一次性购买超过3件，则超过的部分按原价八折付款.如果小明有40元钱，那么他最多可以购买多少件这种商品？

查看试题解析

四、综合题

19. 截至2022年3月27日，全国累计报告接种新型冠状病毒疫苗超过32亿剂次，为了满足市场需求，某公司计划投入10个大、小两种车间共同生产同一种新型冠状病毒疫苗，已知1个大车间和2个小车间每周能生产疫苗共35万剂，2个大车间和1个小车间每周能生产疫苗共40万剂，每个大车间生产1万剂疫苗的平均成本为90万元，每个小车间生产1万剂疫苗的平均成本为80万元.

(1)、该公司每周每个大车间生产疫苗万剂，每个小车间生产疫苗万剂；

(2)、若所有10个车间全部投入生产，且每周生产的疫苗不少于135 万剂，请问共有几种投入方案，请列出所有符合题意的方案，并求出每周生产疫苗的总成本最小值.

查看试题解析
20. 我校举行数学竞赛，一共有25道题，满分100分，每答对一题得4分，答错扣一分，不答记0分.

(1)、某同学只有一道题未作答，最后满分86分，则该生一共答对多少题？

(2)、若规定参赛者每题必须作答，得分大于或等于90分，才可以评为一等奖，则参赛者至少答对多少题才能获评一等奖？

查看试题解析
21. 定义新运算：对于任意实数 $a$ ， $b$ ，都有 $a * b = a (a - b) + 1$ .比如： $2 * 3 = 2 \times (2 - 3) + 1 = 2 \times (- 1) + 1 = - 2 + 1 = - 1$ .

(1)、求 $(- 2) * 1$ 的值.

(2)、若 $3 * x$ 的值小于7，求 $x$ 的取值范围.

查看试题解析
22. 小杰到学校食堂买饭，看到A，B两窗口前面排队的人一样多（设为a人， $a > 8$ ），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人

(1)、此时，若小杰继续在A窗口排队，则他到达窗口还要花的时间是（用含a的代数式表示）

(2)、此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围.（不考虑其它因素）

查看试题解析
23. 某校为积极响应垃圾分类的号召，从商城购进了 $A$ 、 $B$ 两种品牌的垃圾桶用于回收不同种类垃圾.已知 $B$ 品牌垃圾桶比 $A$ 品牌垃圾桶每个贵50元，用3000元购买 $A$ 品牌垃圾桶的数量是用1500元购买 $B$ 品牌垃圾桶数量的4倍.

(1)、求购买一个 $A$ 品牌、一个 $B$ 品牌的垃圾桶各需多少元？

(2)、若该中学准备再次用不超过 $3000$ 元购进 $A$ 、 $B$ 两种品牌垃圾桶共50个，恰逢商场对两种品牌垃圾桶的售价进行了调整： $A$ 品牌按第一次购买时售价的九折出售， $B$ 品牌比第一次购买时售价提高了20%，那么该学校此次最多可购买多少个 $B$ 品牌垃圾桶？

查看试题解析

北师大版2022-2023学年度第二学期八年级数学 一元一次不等式 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期八年级数学一元一次不等式期末复习