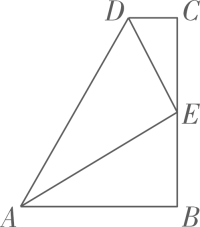北师大版2022-2023学年度第二学期八年级数学 角平分线 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,在中, , 平分 , , , 那么点到直线的距离是( )
 A、 B、 C、 D、2. 如图,中,是角平分线,垂足为 , 垂足为 , 与交于 , 下列说法不一定正确的是( )
A、 B、 C、 D、2. 如图,中,是角平分线,垂足为 , 垂足为 , 与交于 , 下列说法不一定正确的是( ) A、也是中线 B、平分 C、 D、3. 如图,是的平分线,于点 , , , , 则的长是( )
A、也是中线 B、平分 C、 D、3. 如图,是的平分线,于点 , , , , 则的长是( ) A、5 B、6 C、7 D、84. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( )
A、5 B、6 C、7 D、84. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( ) A、2 B、 C、 D、5. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( )
A、2 B、 C、 D、5. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( ) A、5 B、5.5 C、6 D、76. 如图,在中,为角平分线的交点,若的面积为 , 则的面积为( )
A、5 B、5.5 C、6 D、76. 如图,在中,为角平分线的交点,若的面积为 , 则的面积为( ) A、 B、 C、 D、7. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论一定成立的有( )
A、 B、 C、 D、7. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论一定成立的有( )①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③点D在AB的垂直平分线上.
 A、0个 B、1个 C、2个 D、3个8. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC=( )
A、0个 B、1个 C、2个 D、3个8. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC=( ) A、 B、2 C、3 D、+29. 如图,点C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边ΔABC和等边ΔCDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOE=120°;⑥ΔCPQ为等边三角形;⑦CO平分∠AOE;正确的有( )个.
A、 B、2 C、3 D、+29. 如图,点C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边ΔABC和等边ΔCDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOE=120°;⑥ΔCPQ为等边三角形;⑦CO平分∠AOE;正确的有( )个.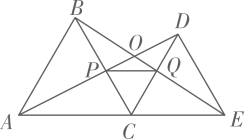 A、3个 B、5个 C、6个 D、7个10. 如图,在中, , AD平分 , 且 , , 点E是AB上一动点,则D,E之间的最小距离为( )
A、3个 B、5个 C、6个 D、7个10. 如图,在中, , AD平分 , 且 , , 点E是AB上一动点,则D,E之间的最小距离为( )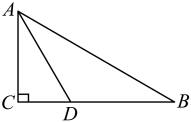 A、8 B、4 C、2 D、1
A、8 B、4 C、2 D、1二、填空题
-
11. 如图,矩形ABCD中,AB=2 ,BC=4,连结对角线AC,E为AC的中点,F为AB边上的动点,连结EF,作点C关于EF的对称点C′,连结C′E,C′F,若△EFC′与△ACF的重叠部分(△EFG)面积等于△ACF的 ,则BF=.
 12. 如图,在中, , 平分于点 , 如果 , 则等于.
12. 如图,在中, , 平分于点 , 如果 , 则等于. 13. 如下图,一把直尺压住射线 , 另一把完全一样的直尺压住射线并且与第一把直尺交于点P,小明说:“射线就是的平分线.”这样说的依据是 .
13. 如下图,一把直尺压住射线 , 另一把完全一样的直尺压住射线并且与第一把直尺交于点P,小明说:“射线就是的平分线.”这样说的依据是 . 14. 如图,AD∥BC,BP平分∠ABC,AP平分∠BAD,PE⊥AB,PE=2,则两平行线AD、BC之间的距离为
14. 如图,AD∥BC,BP平分∠ABC,AP平分∠BAD,PE⊥AB,PE=2,则两平行线AD、BC之间的距离为 15. 如图,点C在的平分线上,于点D,且 , 如果E是射线OB上一点,那么线段CE长度的最小值是 .
15. 如图,点C在的平分线上,于点D,且 , 如果E是射线OB上一点,那么线段CE长度的最小值是 .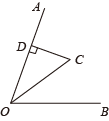
三、解答题
-
16. 已知:如图,是的角平分线.
求证:.
 17. 如图,在中,为其角平分线,于点 , 于点 , 的面积是 , , , 求的长.
17. 如图,在中,为其角平分线,于点 , 于点 , 的面积是 , , , 求的长. 18. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
18. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
四、综合题
-
19. 如图,在中, , , 于E,点F在边上.
 (1)、求证:;(2)、若 , , 求出的面积以及的长.20. 中,AD平分.
(1)、求证:;(2)、若 , , 求出的面积以及的长.20. 中,AD平分.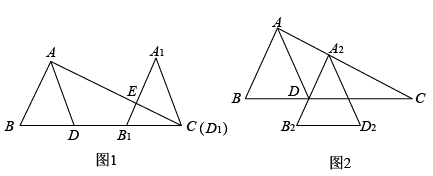 (1)、如图1,将沿BC方向平移,得 , 使得点与点C重合,交AC于点E.求证:;(2)、如图2,将沿着AC方向平移,得到 , 使得经过点D,求证:平分.
(1)、如图1,将沿BC方向平移,得 , 使得点与点C重合,交AC于点E.求证:;(2)、如图2,将沿着AC方向平移,得到 , 使得经过点D,求证:平分.