北师大版2022-2023学年度第二学期八年级数学 线段的垂直平分线 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,在中, , .分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( )
 A、10 B、12 C、14 D、162. 如图,在等腰中, , 垂直平分 , 则的度数等于( )
A、10 B、12 C、14 D、162. 如图,在等腰中, , 垂直平分 , 则的度数等于( )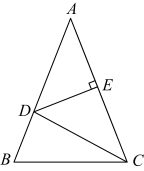 A、 B、 C、 D、3. 如图,在中, , 的垂直平分线交于点E,的垂直平分线交于点F,连接 , 若 , 则的周长是( )
A、 B、 C、 D、3. 如图,在中, , 的垂直平分线交于点E,的垂直平分线交于点F,连接 , 若 , 则的周长是( )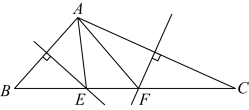 A、5 B、10 C、15 D、204. 如图,在平行四边形中,于点H,E是的中点,F是的中点,已知 , , 则的长为( )
A、5 B、10 C、15 D、204. 如图,在平行四边形中,于点H,E是的中点,F是的中点,已知 , , 则的长为( )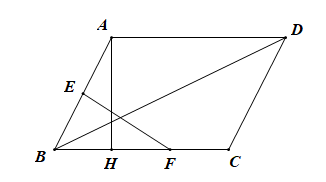 A、 B、 C、 D、5. 观察下列尺规作图痕迹,其中所作线段AD为△ABC的角平分线的是( )A、
A、 B、 C、 D、5. 观察下列尺规作图痕迹,其中所作线段AD为△ABC的角平分线的是( )A、 B、
B、 C、
C、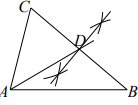 D、
D、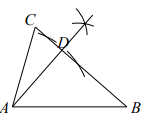 6. 如图,在 ▱ ABCD中,∠B是锐角,点F是AB边的中点,AE⊥BC于点E,连接DF,EF.若∠EFD=90°,AD=2,AB= , 则AE长为( )
6. 如图,在 ▱ ABCD中,∠B是锐角,点F是AB边的中点,AE⊥BC于点E,连接DF,EF.若∠EFD=90°,AD=2,AB= , 则AE长为( ) A、2 B、 C、 D、7. 如图,在中, , 观察图中尺规作图的痕迹,可知的周长为( )
A、2 B、 C、 D、7. 如图,在中, , 观察图中尺规作图的痕迹,可知的周长为( ) A、14 B、15 C、16 D、178. 如图1是由四个全等的直角三角形组成的“风车”图案,其中 , 延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若 , 则该“风车”的面积为( )
A、14 B、15 C、16 D、178. 如图1是由四个全等的直角三角形组成的“风车”图案,其中 , 延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若 , 则该“风车”的面积为( )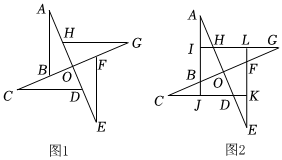 A、 B、 C、 D、9. 如图,在中, , , 分别以A,B两点为圆心,大于为半径画弧,两弧交于M,N两点,直线MN交AC于点D,交于点E,若 , 则AC的长度为( )
A、 B、 C、 D、9. 如图,在中, , , 分别以A,B两点为圆心,大于为半径画弧,两弧交于M,N两点,直线MN交AC于点D,交于点E,若 , 则AC的长度为( )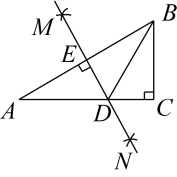 A、9 B、8 C、7 D、610. 依据圆规作图的痕迹,可以用没有刻度的直尺确定的内心的是( )A、
A、9 B、8 C、7 D、610. 依据圆规作图的痕迹,可以用没有刻度的直尺确定的内心的是( )A、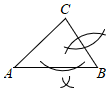 B、
B、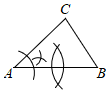 C、
C、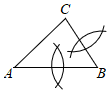 D、
D、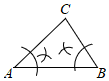
二、填空题
-
11. 如图,在中, , , 分别以点 , 为圆心,大于的长为半径作弧,两弧交于点、 , 作直线交、于点、 , 连接、 , 则.
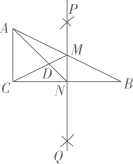 12. 如图,为的边的垂直平分线,交于点D,交于点E,且 , , 则的度数为.
12. 如图,为的边的垂直平分线,交于点D,交于点E,且 , , 则的度数为. 13. 如图,的周长为 , 连接 , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线 , 交边于点E,连接 , 则的周长为 .
13. 如图,的周长为 , 连接 , 分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M,N,作直线 , 交边于点E,连接 , 则的周长为 . 14. 如图,中, , , 垂直平分 , , 则.
14. 如图,中, , , 垂直平分 , , 则.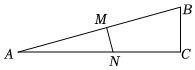 15. 如图,等腰三角形的底边长为4,面积是20,腰的垂直平分线分别交 , 边于 , 点.若点为边的中点,点为线段上一动点,则周长的最小值为 .
15. 如图,等腰三角形的底边长为4,面积是20,腰的垂直平分线分别交 , 边于 , 点.若点为边的中点,点为线段上一动点,则周长的最小值为 .
三、解答题
-
16. 如图,在中, , , 的垂直平分线交边于点 , 交边于点 , 连接 , 求的度数.
 17. 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别是E,F,连接EF,EF与BD相交于点P.求证:EP=FP.
17. 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别是E,F,连接EF,EF与BD相交于点P.求证:EP=FP. 18. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
18. 如图,在中, , 是的垂直平分线,交于点E.已知的周长是24,的长是5.求的周长.
四、综合题
-
19. 如图,在中,.
 (1)、在边上找一点 , 使;(尺规作图,保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若 , , 求的长.20. 如图,在中,垂直平分 , 分别交 , 于点、 , 垂直平分 , 分别交、于点、 , 连接 , .
(1)、在边上找一点 , 使;(尺规作图,保留作图痕迹,不要求写作法和证明)(2)、在(1)的条件下,若 , , 求的长.20. 如图,在中,垂直平分 , 分别交 , 于点、 , 垂直平分 , 分别交、于点、 , 连接 , . (1)、若 , 求的周长等于.(2)、若 , 求的度数21. 如图,某学校(A点)与公路(直线1)的距离为300米,与车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与学校A及车站D的距离相等.
(1)、若 , 求的周长等于.(2)、若 , 求的度数21. 如图,某学校(A点)与公路(直线1)的距离为300米,与车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与学校A及车站D的距离相等. (1)、在图中作出点C;(2)、求商店C与车站D之间的距离.
(1)、在图中作出点C;(2)、求商店C与车站D之间的距离.