北师大版2022-2023学年度第二学期八年级数学 等腰三角形 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,▱ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②OD=AB;③S▱ABCD=AC•CD;④S四边形OECD=S△AOD , 其中成立的个数为( )
 A、1个 B、2个 C、3个 D、4个2. 选择用反证法证明“已知:在中,求证: , 中至少有一个角不大于”时,应先假设( )A、 , B、 , C、 , D、 ,3. 如图,在中, , .分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( )
A、1个 B、2个 C、3个 D、4个2. 选择用反证法证明“已知:在中,求证: , 中至少有一个角不大于”时,应先假设( )A、 , B、 , C、 , D、 ,3. 如图,在中, , .分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点,连接直线 , 分别交、于点、 , 连接 , 则的面积为( ) A、10 B、12 C、14 D、164. 如图,将绕点按逆时针方向旋转 , 得到.若点恰好在线段BC的延长线上,且 , 则旋转角的度数为( )
A、10 B、12 C、14 D、164. 如图,将绕点按逆时针方向旋转 , 得到.若点恰好在线段BC的延长线上,且 , 则旋转角的度数为( ) A、60° B、70° C、100° D、110°5. 如图,在等腰中, , 垂直平分 , 则的度数等于( )
A、60° B、70° C、100° D、110°5. 如图,在等腰中, , 垂直平分 , 则的度数等于( )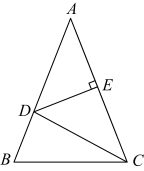 A、 B、 C、 D、6. 如图,将绕点A逆时针旋转得到.若点D在线段的延长线上,则的大小为( )
A、 B、 C、 D、6. 如图,将绕点A逆时针旋转得到.若点D在线段的延长线上,则的大小为( ) A、 B、 C、 D、7. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、 B、 C、 D、7. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点;下列结论:①;②平分;③ , 其中所有正确结论的序号是( ) A、①② B、②③ C、①③ D、①②③8. 如图, , D,E分别是边BC和AC上的点,且 , 若 , 则( )
A、①② B、②③ C、①③ D、①②③8. 如图, , D,E分别是边BC和AC上的点,且 , 若 , 则( ) A、50° B、60° C、70° D、80°9. 如图,在矩形中, , 相交于点O.若 , , 则的长为( )
A、50° B、60° C、70° D、80°9. 如图,在矩形中, , 相交于点O.若 , , 则的长为( ) A、8 B、 C、 D、410. 用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a<b.”时第一步应假设( )A、a>b B、a≥b C、a≤b D、a≠b
A、8 B、 C、 D、410. 用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a<b.”时第一步应假设( )A、a>b B、a≥b C、a≤b D、a≠b二、填空题
-
11. 如图,在▱中,平分交于点 , 连接若 , , 则的度数为.
 12. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设.13. 如图,在中, , , , 将沿射线方向平移2个单位后得到 , 连接 , 则的长为.
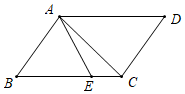
12. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设.13. 如图,在中, , , , 将沿射线方向平移2个单位后得到 , 连接 , 则的长为. 14. 如图,为的边的垂直平分线,交于点D,交于点E,且 , , 则的度数为.
14. 如图,为的边的垂直平分线,交于点D,交于点E,且 , , 则的度数为. 15. 如果一个等腰三角形的两边长分别为2和4,则第三边的长为.
15. 如果一个等腰三角形的两边长分别为2和4,则第三边的长为.三、解答题
-
16. 如图,在四边形中, , , , 点为上一点,连接 , 交于点 , .判断的形状,并说明理由.
 17. 已知:如图,中,是中点,垂足为 , 垂足为 , 且 , 求证:是等腰三角形
17. 已知:如图,中,是中点,垂足为 , 垂足为 , 且 , 求证:是等腰三角形 18. 在等边的三条边上,分别取点D,E,F,使得 , 连接 , 求证:是等边三角形.
18. 在等边的三条边上,分别取点D,E,F,使得 , 连接 , 求证:是等边三角形.
四、综合题
-
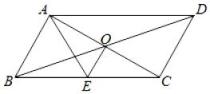
19. 如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
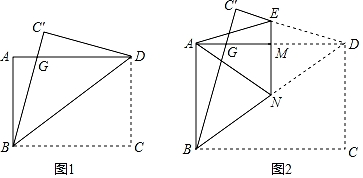 (1)、求证:BG=DG;(2)、求C′G的长;(3)、如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.20. 已知:菱形的边长为 , .把一个含的三角尺与这个菱形叠合,如果使三角形的顶点与点重合,三角尺的两边与菱形的两边 , 分别相交于点 , (点 , 不与端点重合).
(1)、求证:BG=DG;(2)、求C′G的长;(3)、如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.20. 已知:菱形的边长为 , .把一个含的三角尺与这个菱形叠合,如果使三角形的顶点与点重合,三角尺的两边与菱形的两边 , 分别相交于点 , (点 , 不与端点重合). (1)、如图1,求证:;(2)、如图2,连接 , 求面积的最大值;(3)、如图3,连接 , 与 , 相交于点 , .若以线段 , , 为边组成的三角形是直角三角形,求的值.21. 如图,在梯形中, , .
(1)、如图1,求证:;(2)、如图2,连接 , 求面积的最大值;(3)、如图3,连接 , 与 , 相交于点 , .若以线段 , , 为边组成的三角形是直角三角形,求的值.21. 如图,在梯形中, , . (1)、尺规作图:在上找一点E,连接 , 使得;(不写作法,保留作图痕迹)(2)、在(1)条件下,若 , , , 求梯形的高.
(1)、尺规作图:在上找一点E,连接 , 使得;(不写作法,保留作图痕迹)(2)、在(1)条件下,若 , , , 求梯形的高.