北师大版2022-2023学年度第二学期七年级数学 等可能事件的概率 期末复习
试卷更新日期：2023-05-15 类型：复习试卷
一、单选题
-
1. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字外其他均相同，将它们背面朝上，从中任抽一张，抽到负数的概率是（ ）A、 B、 C、 D、2. 如图，一只小狗在如图所示的方砖上走来走去，最终停留在阴影方砖上的概率是（ ）
A、 B、 C、 D、3. 如图是由边长为1的小正方形组成的网格，若在这个网格面上随意抛一粒豆子，则豆子落在阴影区域的概率为（ ）
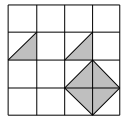A、 B、 C、 D、4. 某小组做“当试验次数很大时，用频率估计概率”的试验时，统计了某一结果出现的频率，表格如下，则符合这一结果的试验最有可能是（ ）次数
100
200
300
400
500
600
700
800
900
1000
频率
0.60
0.30
0.50
0.36
0.42
0.38
0.41
0.39
0.40
0.40
A、掷一个质地均匀的骰子，向上的面点数是“6” B、掷一枚一元的硬币，正面朝上 C、不透明的袋子里有2个红球和3个黄球，除颜色外都相同，从中任取一球是红球 D、三张扑克牌，分别是3，5，5，背面朝上洗匀后，随机抽出一张是55. 小明有两根长度分别为5cm和8cm的木棒，他想钉一个三角形的木框.现有5根木棒供他选择，其长度分别为.小明随手拿了一根，恰好能够组成一个三角形的概率为（ ）A、 B、 C、 D、16. 在同一副扑克牌中抽取2张“黑桃”，5张“梅花”，3张“方块”，将这10张牌背面朝上洗匀，从中任意抽取1张，是“方块”的概率为（ ）A、 B、 C、 D、7. 已知现有的9瓶饮料中有3瓶已过了保质期，从这9瓶饮料中随机抽取1瓶，恰好取到已过了保质期的饮料的概率是（ ）A、 B、 C、 D、8. 一个质量均匀的正方体骰子，六个面分别标有1，2，3，4，5，6，任意掷一次骰子，掷出结果为“2的倍数”的概率为（ ）A、 B、 C、 D、9. 小球在如图所示的地板上自由地滚动，随机地停留在某块方砖上，最终停在白色区域上的概率是（ ）
A、 B、 C、 D、10. 一个小球在如图所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大质地完全相同，则该小球最终停留在阴影区域的概率是（ ）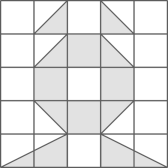
A、 B、 C、 D、二、填空题
-
11. 一只蚂蚁自由自在地在用七巧板拼成的正方形中爬来爬去（每块七巧板的表面完全相同），它最终停留在1号七巧板上的概率 ．
12. 如图是一个寻宝游戏的戴宝图，分别有“花朵”，“太阳”，“月亮”三种图案，宝物（只有一个）藏在“月亮”下的概率是 ．
13. 长度分别为3cm，4cm，5cm，9cm的四条线段，任取其中三条能组成三角形的概率是 ．14. 事件A发生的概率为 ， 大量重复做这种试验，事件A平均每1000次发生的次数是 ．15. 在一个不透明的袋子里装有红球、黄球共16个，这些球除颜色外都相同，小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是；三、解答题
-
16. 某校欲举办文艺汇演活动，小丽和小芳都想当节目主持人，但现在只有一个名额.小丽想出了一个办法，她将一个转盘(质地均匀)平均分成6份.如图所示，游戏规定：随意转动转盘，若指针指到3，则小丽去；若指针指到2，则小芳去；若指针指到其他数字或指在线上，则重转.这个游戏规定对双方公平吗?为什么?若不公平，请修改游戏规定，使这个游戏对双方公平.
17. 为纪念中国共青团成立100周年，校团委举办“走进百年团史，追寻信仰之光”知识竞赛，并设立了一个可以自由转动的转盘（如图所示），每位参赛同学都有一次转动转盘的机会．已知该转盘被等分成16个扇形，当转盘停止后，若指针正好对准红色、黄色、绿色区域，就可以分别获得笔记本、签字笔或书签作纪念品．小华参加知识竞赛后，转动一次转盘，他获得纪念品的概率是多少？
18. 学校举办了书法比赛．小明和小张都想参加，但现在只有一个名额．小明想出了一个办法，他将一个转盘（质地均匀）平均分成6份，如图所示．游戏规定：随意转动转盘，若指针指到1，2，3中任一个数，则小明去；若指针指到其它数，则小张去．这个游戏规定对双方公平吗？为什么？若不公平，请修改游戏规定，使这个游戏对双方公平．
四、综合题
-
19. 小明和小亮两位同学做掷骰子（质地均匀的正方体）游戏，他们共做了100次试验，结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
16
14
25
20
12
13
(1)、计算“1点朝上”的频率和“6点朝上”的频率；(2)、小亮说：“若投掷1000次，则出现4点朝上的次数正好是200次”．小亮的说法符合题意吗？(3)、小明将一枚骰子任意投掷一次，求朝上的点数不小于4的概率．20. 小明家里的阳台地面，水平铺设了仅黑白颜色不同的18块方砖（如图），他从房间里向阳台抛小皮球，小皮球最终随机停留在某块方砖上．
(1)、求小皮球分别停留在黑色方砖与白色方砖上的概率；(2)、上述哪个概率较大？要使这两个概率相等，应改变第几行第几列的哪块方砖颜色？怎样改变？21. 一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出1个球是红球的概率为 ．(1)、求口袋中黄球的个数；(2)、现规定：摸到红球得5分，摸到黄球得3分，摸到蓝球得2分（每次摸后放回），乙同学在一次摸球游戏中，第一次随机摸到一个红球第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学三次摸球所得分数之和不低于10分的概率．22. 在一个不透明的袋子中装有个红球和个黄球，这些球除颜色外都相同，将袋子中的球充分摇匀后，随机摸出一球．
(1)、分别求出摸出的球是红球和黄球的概率．(2)、为了使摸出两种球的概率相同，再放进去个同样的红球或黄球，那么这个球中红球和黄球的数量分别应是多少？23. 一口袋中有5张完全相同的卡片，分别写有1cm、2cm、3cm、4cm和5cm，口袋外有2张卡片，分别写有3cm和5cm．现随机从袋内取出一张卡片，与口袋外两张卡片放在一起，以卡片上的数量分别作为三条线段的长度．(1)、求这三条线段能构成三角形的概率；(2)、求这三条线段能构成等腰三角形的概率．