北师大版2022-2023学年度第二学期七年级数学 感受可能性 期末复习

试卷更新日期：2023-05-15 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 下列说法错误的是（       ）
    A、“从一个只有红球的袋子里面摸出一个球是红球”是必然事件 B、如果明天降水的概率是50% ， 那么明天有半天都在降雨 C、“随意掷两个均匀的骰子，朝上面的点数之和为13”是不可能事件 D、随机事件发生的概率介于0和1之间

    查看试题解析

  • 2. 下列事件中，随机事件是（ ）
    A、购买一张福利彩票中奖了 B、通常水加热到100​∘C时会沸腾 C、在地球上，抛出的篮球会下落 D、郑一枚㳙子，向上一面的字数一定大于零

    查看试题解析

  • 3. 下列诗词所描述的事件，不属于随机事件的是（）
    A、黄梅时节家家田，青草池塘处处蛙 B、人间四月芳菲尽，山寺桃花始盛开 C、三月残花落更开，小檐日日燕飞来 D、水面上秤锤浮，直待黄河彻底枯

    查看试题解析

  • 4. 下列事件中是必然事件的是（  ）
    A、打开电视机，正在播放《新闻联播》 B、某种彩票中奖概率为1%，买100张该种彩票一定会有一张中奖 C、投掷一枚质地均匀的硬币100次，正面朝上的次数为50次 D、367个同学参加一个集会，他们中至少有两个同学的生日是同月同日

    查看试题解析

  • 5. 经过有交通信号灯的路口，遇到红灯．这个事件是（  ）
    A、必然事件 B、不可能事件 C、随机事件 D、确定性事件

    查看试题解析

  • 6. “购买1张彩票，恰好中奖”这个事件是（ ）
    A、随机事件 B、确定事件 C、不可能事件 D、必然事件

    查看试题解析

  • 7. 事件“掷一枚质地均匀的硬币，硬币落下后，正面朝上”是（  ）
    A、必然事件 B、确定事件 C、随机事件 D、不可能事件

    查看试题解析

  • 8. 下列事件中是不可能事件的是（       ）
    A、从一副扑克牌中任抽一张牌恰好是“红桃” B、在装有白球和黑球的袋中摸球，摸出了红球 C、2022年大年初一早晨艳阳高照 D、从两个班级中任选三名学生，至少有两名学生来自同一个班级

    查看试题解析

  • 9. 下列事件是随机事件事件的是（  ）
    A、瓜熟蒂落 B、水中捞月 C、守株待兔 D、缘木求鱼

    查看试题解析

  • 10. 下列事件中，确定事件是（  ）
    A、打开电视机，正在播放广告 B、买一张电影票，座位号是奇数号 C、3天内会下雨 D、13个人中至少有2人生日在同一个月

    查看试题解析

二、填空题

  • 11. 芬芬任意买一张电影票的座位号是偶数是事件（填随机或必然或不可能）

    查看试题解析

  • 12. 一个不透明的袋子里有3个红球和5个白球，每个球除颜色外都相同，从袋中任意摸出一个球，那么摸到红球的可能性比摸到白球的可能性 ． （填“大”“小”或“相同”）

    查看试题解析

  • 13. “在只装有黑色围棋的盒子中摸出一颗白棋”是事件．（填“随机”“必然”或“不可能”）

    查看试题解析

  • 14. “小明投篮一次，投进篮筐”，这一事件是事件．（填“随机”或“必然”或“不可能”）

    查看试题解析

  • 15. 从一副扑克牌中任意抽一张扑克牌，是红桃2，此事件是事件．（填“必然”“随机”或“不可能”）

    查看试题解析

三、解答题

  • 16. 某商人制成了一个如图所示的转盘，取名为“开心大转盘”，游戏规定：参与者自由转动转盘，转盘停止后，若指针指向字母“A”，则收费2元，若指针指向字母“B”，则奖励3元；若指针指向字母“C”，则奖励1元.一天，前来寻开心的人转动转盘80次，你认为该商人是盈利的可能性大还是亏损的可能性大？为什么？

    查看试题解析

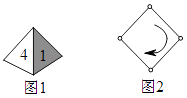
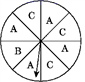  • 17. 如图1，一枚质地均匀的正四面体骰子，它有四个面．并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏则每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D．若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B．…

    设游戏这从圈A起跳．嘉嘉随机掷一次骰子．淇淇随机掷两次骰子．请问嘉嘉与淇淇掷完骰子落回到圈A的可能性一样吗？回答问题并说明理由．

    查看试题解析

  • 18. 有两个盒子，分别装有若干个除颜色外都相同的球，第一个盒子装有4个红球和6个白球，第二个盒子装有6个红球和6个白球．分别从这两个盒子中各摸出1个球，请你通过计算来判断从哪一个盒子中摸出白球的可能性大．

    查看试题解析

四、综合题

  • 19. 小明和小亮两位同学做掷骰子（质地均匀的正方体）游戏，他们共做了100次试验，结果如下：

    朝上的点数

    1

    2

    3

    4

    5

    6

    出现的次数

    16

    14

    25

    20

    12

    13

    (1)、计算“1点朝上”的频率和“6点朝上”的频率；
    (2)、小亮说：“若投掷1000次，则出现4点朝上的次数正好是200次”．小亮的说法符合题意吗？
    (3)、小明将一枚骰子任意投掷一次，求朝上的点数不小于4的概率．

    查看试题解析

  • 20. 在一个不透明的袋子中装有4个红球和6个白球，每个球除颜色外其余都相同．
    (1)、从中任意摸出1个球，摸到球的可能性大；
    (2)、摸出红球和白球的概率分别是多少？
    (3)、如果另拿红球和白球共8个放入袋中并搅匀，使得从中任意摸出1个球，摸到红球和白球的可能性大小相等，那么应放入个红球，个白球．

    查看试题解析

  • 21. 如图，现有一个圆形转盘被平均分成6等份，分别标有2、3、4、5、6、7这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字．

    (1)、转到数字9是 ， 转到数字6是 ， （从“随机事件”、“必然事件”、“不可能事件”选一个填入）
    (2)、转动转盘一次，转出的数字是3的倍数的概率是多少？
    (3)、现有两张分别写有2和5的卡片，随机转动转盘一次，转盘停止后记下转出的数字，与两张卡片上的数字分别作为三条线段的长度（长度单位均是厘米），这三条线段能构成三角形的概率是多少？

    查看试题解析

  • 22. 如图，现有一个圆形转盘被平均分成6份，分别标有3、4、5、6、7、8这六个数字，转动转盘，当转盘停止时，指针指向的数字即为转出的数字（若指针指向分界线，则重新转），求：

    (1)、转到数字5是事件；（填“随机”、“必然”或“不可能”）
    (2)、转动转盘一次，转出的数字为偶数的概率是多少？
    (3)、若小明转动两次后分别转到的数字是3和7，小明再转动一次，转出的数字与前两次转出的数字分别作为三条线段（长度单位均相同），求这三条线段能构成三角形的概率．

    查看试题解析

  • 23. 如图，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：每购买500元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针上对准500、200、100、50、10的区域，顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份，如果指针恰好停在分割线上，那么重转一次，直到指针指向某一区域为止).

    (1)、小华购物450元，他获得购物券的概率是多少?
    (2)、小丽购物600元，那么：

    ①她获得50元购物券的概率是多少?

    ②她获得100元以上(包括100元)购物券的概率是多少?

    查看试题解析