北师大版2022-2023学年度第二学期七年级数学 利用轴对称进行设计 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
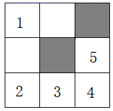
1. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的编号1-5的小正方形中任意一个涂黑,则所得图案是一个轴对称图形的概率是( )
 A、1 B、 C、 D、2. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
A、1 B、 C、 D、2. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、 B、
B、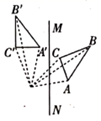 C、
C、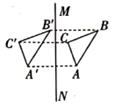 D、
D、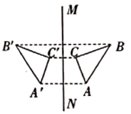 3. 如图,图①,图②,图③,图④这四个图形中,可以由图A平移得到的是( )
3. 如图,图①,图②,图③,图④这四个图形中,可以由图A平移得到的是( )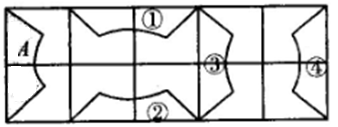 A、图① B、图② C、图③ D、图④4. 如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
A、图① B、图② C、图③ D、图④4. 如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( ) A、7个 B、8个 C、9个 D、10个5. 下列剪纸作品中,是轴对称图形的为( )A、
A、7个 B、8个 C、9个 D、10个5. 下列剪纸作品中,是轴对称图形的为( )A、 B、
B、 C、
C、 D、
D、 6. 在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有( )
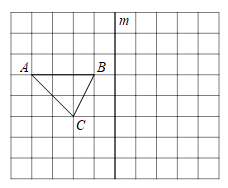
6. 在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有( ) A、5种 B、7种 C、9种 D、10种7. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( )
A、5种 B、7种 C、9种 D、10种7. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( ) A、1个 B、2个 C、3个 D、4个8. 如图,点A,B在方格纸的格点位置上,若要再找一个格点C,使它们所构成的三角形为轴对称图形,则这样的格点C在图中共有( )
A、1个 B、2个 C、3个 D、4个8. 如图,点A,B在方格纸的格点位置上,若要再找一个格点C,使它们所构成的三角形为轴对称图形,则这样的格点C在图中共有( )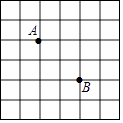 A、4个 B、6个 C、8个 D、10个9. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A、4个 B、6个 C、8个 D、10个9. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )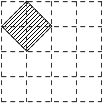 A、2种 B、3种 C、4种 D、5种10.
A、2种 B、3种 C、4种 D、5种10.如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分)是轴对称图形,其中涂法有( )
 A、6种 B、7种 C、8种 D、9种
A、6种 B、7种 C、8种 D、9种二、填空题
-
11. 如图“3×3”网格中,有3个涂成黑色的小方格,若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称的概率是 .
 12. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个.
12. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个. 13. 如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同的涂法.
13. 如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同的涂法.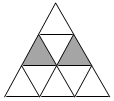 14. 如图所示,由小正方形组成的“7”字形图中,请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形.
14. 如图所示,由小正方形组成的“7”字形图中,请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形. 15. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法.
15. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法.
三、解答题
-
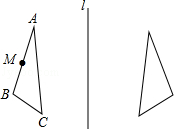
16. 如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
 17. 利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.
17. 利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.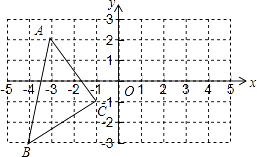 18. 如图,在每个小正方形的边长为1的网格中,点A、B、C、D均在格点上,点P是直线CD上的点连BP,点A′是点A关于直线BP的对称点
18. 如图,在每个小正方形的边长为1的网格中,点A、B、C、D均在格点上,点P是直线CD上的点连BP,点A′是点A关于直线BP的对称点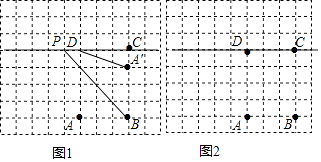
(Ⅰ)在图①中,当DP=1(点P在点D的左侧)时,计算DA′的值;
(Ⅱ)当DA′取值最小值时,请在如图②所示的网格中,用无刻度的直尺画出点A′,并简要说明点A′的位置如何找到的(不要求证明)
四、综合题
-
19. 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段和直线 , 点 , , , 均在小正方形的顶点上.
 (1)、在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点 , 点的对称点为点;(2)、利用网格计算四边形的面积.20. 如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)、在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点 , 点的对称点为点;(2)、利用网格计算四边形的面积.20. 如图,方格图中每个小正方形的边长为1,点A,B,C都是格点. (1)、画出△ABC关于直线MN对称的△A1B1C1;(2)、写出AA1的长度.21. 如图,在正方形网格中,是格点三角形.
(1)、画出△ABC关于直线MN对称的△A1B1C1;(2)、写出AA1的长度.21. 如图,在正方形网格中,是格点三角形.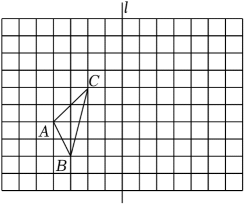 (1)、画出 , 使得和关于直线对称;(2)、请在直线上找一点(即画出点),使点到点和点的距离之和最小;(3)、求的面积.
(1)、画出 , 使得和关于直线对称;(2)、请在直线上找一点(即画出点),使点到点和点的距离之和最小;(3)、求的面积.