北师大版2022-2023学年度第二学期七年级数学 简单的轴对称图形 期末复习
试卷更新日期：2023-05-15 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，∠BAC＝∠ABC＝42°，过点C作CD⊥AB于点D，点E是CD上一点，将△ACE沿着AE翻折得到△AFE，连接CF，若E，F，B三点恰好在同一条直线上，则∠CFA的度数是（ ）
A、75° B、78° C、80° D、84°2. 如图，在△ABC中，∠C=90°，∠1=∠2，BC=16cm，点D到AB的距离为6cm，则BD的长为（ ）
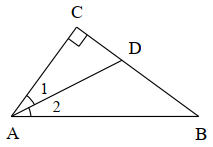A、 B、 C、 D、3. 如图，将△ABC沿过边上两点D，E的直线折叠后，使得点B与点A重合，若已知BE＝4cm，则△ABC的周长与△ADC的周长的差为（ ）
A、4cm B、5cm C、8cm D、10cm4. 如图，将△ABC绕点A顺时针旋转角100°，得到△ADE，若点E恰好在CB的延长线上，则∠BED的度数为（ ）
A、80° B、70° C、60° D、50°5. 一个等腰三角形的三边长分别为3cm、acm、6cm，则它的周长是（ ）A、12cm B、15cm C、12cm或15cm D、不能确定6. 已知等腰△ABC中，∠A＝50°，则∠B的度数为（ ）A、50° B、65° C、50°或65° D、50°或65°或80°7. 如图，在△ABC中，DE垂直平分BC，若∠CDE＝64°，∠A＝28°，则∠ABD的度数为（ ）
A、100° B、128° C、108° D、98°8. 如图，在△ABC中，∠ACB＝90°，BE平分∠ABC，DE⊥AB于D．如果AC＝10cm，那么AE+DE等于（ ）
A、6cm B、8cm C、10cm D、12cm9. 如图，在△ABC中，AB＝3BC，BD平分∠ABC交AC于点D，若△ABD的面积为S1 ， △BCD的面积为S2 ， 则关于S1与S2之间的数量关系，下列说法正确的是（ ）
A、S1＝4S2 B、S1＝3S2 C、S1＝2S2 D、S1＝S210. 如图，将绕点A按逆时针方向旋转100°得到（点的对应点是点 ， 点的对应点是点），连接 ， 若 ， 则的度数为（ ）
A、20° B、30° C、40° D、45°二、填空题
-
11. 如图， ， ， 点、分别是线段和上的动点，在两点运动到某一位置时，恰好使得 ， 此时量得 ， ， ， 则.
12. 如图，射线OC是∠AOB的平分线，P是射线OC上一点，PD⊥OA于点D，DP＝6，若E是射线OB上一点，OE＝4，则△OPE的面积是 ．
13. 如图，在中， ， 利用尺规在 ， 上分别截取；分别以点M，N为圆心，以大于的长为半径作弧，两弧在内部交于点E；作射线交于点F．若 ， 点H为线段上的一动点，则的最小值是 ．
14. 如图，在△ABC中，DF，EM分别垂直平分边AB，AC，若△AFM的周长为9，则BC= ．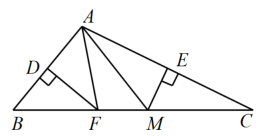
15. 如图，在中， ， M是AB的中点，交AC于点N，的周长是7cm，则BC的长为 ．
三、解答题
-
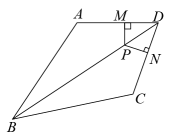
16. 如图所示，已知BD为∠ABC的平分线，AB＝BC，PM⊥AD于点M，PN⊥CD于点N．
求证：
17. 如图，在△ABC中，AB＝AC，AD为BC边上的中线，∠CAD＝40°，EF为过点A的一条直线，且EF∥BC，求∠BAE的度数．
18. 如图，在△ABC中，∠A＝40°，AB＝AC，点D为AC上任意一点，若△BCD是以BC为腰的等腰三角形，求∠BDC的度数．
四、综合题
-
19. 已知：如图，∠ABD和∠BDC的平分线交于点E，BE交CD于点F，∠1＋∠2＝90°.
(1)、试说明：ABCD；(2)、试探究DF与DB的数量关系，并说明理由.20. 如图，在Rt△ABC和Rt△EFD中，∠ABC＝∠EFD＝90°，AC＝ED，AC⊥ED，垂足为M，连接AE、CE．
(1)、△ABC与△EFD全等吗？为什么？(2)、若∠AEF＝∠DEF，判断∠AEC与∠ACE的数量关系，并说明理由．21. 如图，已知△ABC是等腰三角形，CA＝CB，∠ACB是锐角，∠ACB＝α．点M在边AC上，点N在边BC上（点M、点N不与所在线段端点重合），BN＝AM，连接AN，BM，射线AG∥BC，延长BM交射线AG于点D，点E在NA的延长线上，且AE＝DE．
(1)、△BCM与△ACN全等吗？请说明理由；(2)、请求出∠BDE的度数．（用含α的代数式表示）
