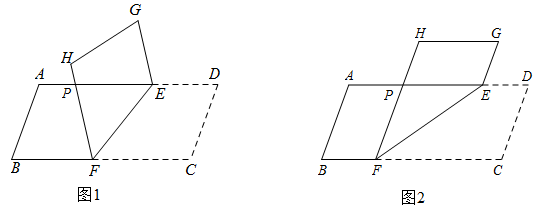北师大版2022-2023学年度第二学期七年级数学 探索轴对称的性质 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( )
 A、140° B、120° C、110° D、100°2. 如图,将长方形纸片沿折叠后,若 , 则的度数为( )
A、140° B、120° C、110° D、100°2. 如图,将长方形纸片沿折叠后,若 , 则的度数为( )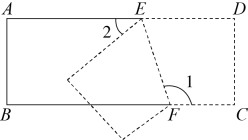 A、 B、 C、 D、3. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、 , 若 , , 则的度数是( )
A、 B、 C、 D、3. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、 , 若 , , 则的度数是( ) A、 B、 C、 D、4. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( )
A、 B、 C、 D、4. 如图,已知 , 点E,F分别在直线上,点P在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为( ) A、 B、 C、或 D、或或5. 如图,长方形纸片ABCD分别沿着EF、DH折叠后,点A,B,C分别落在点A′,B′,C′的位置,当DA'∥B'C'时,∠1=67°,则∠2=( ).
A、 B、 C、或 D、或或5. 如图,长方形纸片ABCD分别沿着EF、DH折叠后,点A,B,C分别落在点A′,B′,C′的位置,当DA'∥B'C'时,∠1=67°,则∠2=( ). A、23° B、46° C、56° D、67°6. 将一张长方形纸片沿EF折叠,折叠后的位置 如图所示,若∠EFB=65°,则∠AED′等于( )
A、23° B、46° C、56° D、67°6. 将一张长方形纸片沿EF折叠,折叠后的位置 如图所示,若∠EFB=65°,则∠AED′等于( )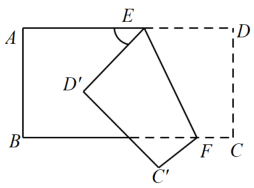 A、70° B、65° C、50° D、25°7. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )
A、70° B、65° C、50° D、25°7. 某同学在一次数学实践活动课中将-条对边互相平行的纸带进行两次折叠(如图) .折痕分别为AB,CD,若CD∥BE,且∠CBE=∠ABC,则∠1为( )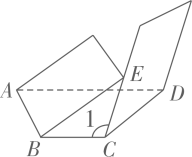 A、106° B、108° C、109° D、110°8. 如图,将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=56°,则∠AED的度数是( )
A、106° B、108° C、109° D、110°8. 如图,将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=56°,则∠AED的度数是( ) A、62° B、50° C、75° D、55°9. 如图,把一张长方形的纸按图那样折叠后,B,C两点落在B1 , C1处,若∠AEB1=70,则∠BEF=( )
A、62° B、50° C、75° D、55°9. 如图,把一张长方形的纸按图那样折叠后,B,C两点落在B1 , C1处,若∠AEB1=70,则∠BEF=( ) A、70° B、60° C、65° D、55°10. 如图,将长方形沿线段折叠到的位置,若 , 则的度数为( )
A、70° B、60° C、65° D、55°10. 如图,将长方形沿线段折叠到的位置,若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在四边形纸片中 , 将纸片折叠,点、分别落在、处,折痕为 , 与交于点.若 , 则的度数为.
 12. 如图,已知长方形纸片 , 点E,F在BC边上,点G,H在边上,分别沿折叠,点B和点C 恰好都落在点P处.若 , 则.
12. 如图,已知长方形纸片 , 点E,F在BC边上,点G,H在边上,分别沿折叠,点B和点C 恰好都落在点P处.若 , 则. 13. 如图,长方形纸片ABCD,M为AD边上一点,将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠AMB=35°,∠1=40°,则∠MCB的度数为°
13. 如图,长方形纸片ABCD,M为AD边上一点,将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠AMB=35°,∠1=40°,则∠MCB的度数为° 14. 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=°.
14. 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=°. 15. 长方形如图折叠,D点折叠到D′的位置.已知∠D′FC=76°,则∠EFC= .
15. 长方形如图折叠,D点折叠到D′的位置.已知∠D′FC=76°,则∠EFC= .
三、解答题
-
16. 如图,把一个长方形纸片沿EF折叠后,点D、C分别落在点D'、C'的位置,且D'C'交BC于点M,若∠EFB=56°,求∠BMD'的度数.
 17. 如图,长方形纸片 , 点为边的中点,将纸片沿折叠,点的对应点为 , 连接求证:∥ .
17. 如图,长方形纸片 , 点为边的中点,将纸片沿折叠,点的对应点为 , 连接求证:∥ . 18. 如图,长方形纸片 , 点E为边的中点,将纸片沿折叠,点的对应点为 , 连接 . 求证:
18. 如图,长方形纸片 , 点E为边的中点,将纸片沿折叠,点的对应点为 , 连接 . 求证:
四、综合题
-
19. 如图,在中, , , , , 点D在边上,将沿折叠,使点A恰好落在边上的点处.
 (1)、求的周长;(2)、若 , 求的度数.20. 已知 , 点A在射线CE上,把沿AB翻折得 , .
(1)、求的周长;(2)、若 , 求的度数.20. 已知 , 点A在射线CE上,把沿AB翻折得 , . (1)、若 , 则的度数为°;(2)、设 , ,
(1)、若 , 则的度数为°;(2)、设 , ,①如图1,当点D在直线CE左侧时,求y与x的数量关系,并写出x的取值范围;
②如图2,当点D在直线CE右侧时出y与x的数量关系是 ▲ ;
(3)、过点D作//交CE于点F,当时,求的度数.21. 如图,在中, , , 于D,点E为BC边上一点,连接AE.把沿着AE对折后,点B的对应点刚好落在AC边上的点F处.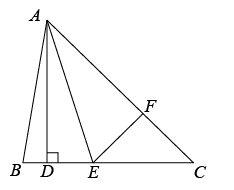 (1)、求∠FEC的度数;(2)、求∠DAE的度数.
(1)、求∠FEC的度数;(2)、求∠DAE的度数.