湖北省十堰市郧阳区2023年中考数学质检试卷(3月份)
试卷更新日期:2023-05-15 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. ( )A、2023 B、-2023 C、 D、2. 如图是由五个相同的小正方体搭成的一个几何体,它的主视图是( )
 A、
A、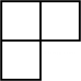 B、
B、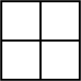 C、
C、 D、
D、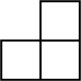 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,某同学在做“剪纸”活动时发现一个有趣的现象:把一个长方形纸片沿虚线剪开得到的五边形周长小于原长方形周长能正确解释这一现象的数学知识是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,某同学在做“剪纸”活动时发现一个有趣的现象:把一个长方形纸片沿虚线剪开得到的五边形周长小于原长方形周长能正确解释这一现象的数学知识是( )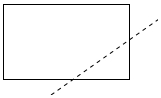 A、过一点有无数条直线 B、两点之间线段最短 C、两点确定一条直线 D、以上说法都不正确5. 某课外学习小组有5人,在一次数学测验中的成绩分别是:120,100,135,100,125,则他们的成绩的平均数和众数分别是( )A、116和100 B、116和125 C、106和120 D、106和1356. 我国明代数学读本算法统宗中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两问客人有几人?设客人有人,则可列方程为( )A、 B、 C、 D、7. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度的地方即同时使 , , 然后张开两脚,使、两个尖端分别在线段的两个端点上,若 , 则的长是( )
A、过一点有无数条直线 B、两点之间线段最短 C、两点确定一条直线 D、以上说法都不正确5. 某课外学习小组有5人,在一次数学测验中的成绩分别是:120,100,135,100,125,则他们的成绩的平均数和众数分别是( )A、116和100 B、116和125 C、106和120 D、106和1356. 我国明代数学读本算法统宗中有一道题,其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,还差8两问客人有几人?设客人有人,则可列方程为( )A、 B、 C、 D、7. 如图,比例规是伽利略发明的一种画图工具,使用它可以把线段按一定比例伸长或缩短,它是由长度相等的两脚和交叉构成的.如果把比例规的两脚合上,使螺丝钉固定在刻度的地方即同时使 , , 然后张开两脚,使、两个尖端分别在线段的两个端点上,若 , 则的长是( ) A、 B、 C、 D、8. 如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A、 B、 C、 D、8. 如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )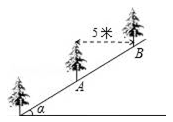 A、5cosα B、 C、5sinα D、9. 如图,以的边为直径的恰好过的中点 , 过点作于 , 连接 , 则下列结论中:;;; , 其中一定正确的结论有( )
A、5cosα B、 C、5sinα D、9. 如图,以的边为直径的恰好过的中点 , 过点作于 , 连接 , 则下列结论中:;;; , 其中一定正确的结论有( )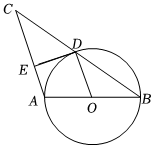 A、1个 B、2个 C、3个 D、4个10. 如图,点是二次函数图象上的一点,且位于第一象限,点是直线上一点,点与点关于原点对称,连接 , , 若为等边三角形,则点的坐标是( )
A、1个 B、2个 C、3个 D、4个10. 如图,点是二次函数图象上的一点,且位于第一象限,点是直线上一点,点与点关于原点对称,连接 , , 若为等边三角形,则点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 2022年5月10日凌晨,长征7号火箭托举着天舟四号货运飞船发射升空,在距地面390000米的高度,与空间站完成自主交会对接任务390000用科学记数法表示为 .12. 不等式的解集为 .13. 小聪和小明两个同学玩“石头,剪刀、布“的游戏,随机出手一次是平局的概率是.14. 将字母“”,“”按照所示的规律摆放,依次下去,则第10个图形中“”的个数是 .
 15. 如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是 .
15. 如图,在半径AC为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则图中阴影部分的面积是 .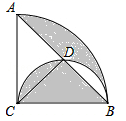 16. 【阅读材料】平面几何中的费马问题是十七世纪法国数学家皮埃尔德费马提出的一个著名的几何问题:给定不在一条直线上的三个点、、 , 求平面上到这三个点的距离之和最短的点的位置,费马问题有多种不同的解法,最简单快捷的还是几何解法如图1,我们可以将绕点顺时针旋转得到 , 连接 , 可得为等边三角形,故 , 由旋转可得 , 因 , 由两点之间线段最短可知,的最小值与线段的长度相等.
16. 【阅读材料】平面几何中的费马问题是十七世纪法国数学家皮埃尔德费马提出的一个著名的几何问题:给定不在一条直线上的三个点、、 , 求平面上到这三个点的距离之和最短的点的位置,费马问题有多种不同的解法,最简单快捷的还是几何解法如图1,我们可以将绕点顺时针旋转得到 , 连接 , 可得为等边三角形,故 , 由旋转可得 , 因 , 由两点之间线段最短可知,的最小值与线段的长度相等.【解决问题】如图2,在直角三角形内部有一动点 , , , 连接 , , , 若 , 求的最小值 .

三、解答题(本大题共9小题,共72.0分。)
-
17. 计算:18. 先化简,再求值: ,其中 .19. 已知一次函数与反比例函数的图象交于、两点.
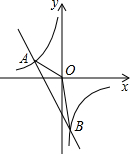 (1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、结合图象直接写出不等式的解集.20. 某校七年级数学备课组在“互联网”教学模式下进行一元一次方程章节教学前,设计了如下四种预习方案:
(1)、求一次函数和反比例函数的表达式;(2)、求的面积;(3)、结合图象直接写出不等式的解集.20. 某校七年级数学备课组在“互联网”教学模式下进行一元一次方程章节教学前,设计了如下四种预习方案:方案教材预习
方案导学案预习
方案导学案课外教辅资料预习
方案前置学习单课前微课预习
为达到良好的预习效果,备课组教师将上述预习方案作为调查内容发到全年级800名同学手中,要求每位同学选出自己最喜欢的一种,他们随机抽取部分学生的调查问卷进行统计,并根据统计数据画出如下不完整的两幅统计图.

请根据已有的信息完成下列任务:
(1)、备课组教师抽取了 名学生的调查问卷;(2)、计算扇形统计图中方案的圆心角的度数是 ▲ , 并补全条形统计图;(3)、估计该校七年级同学中选择“方案”这种预习方案的有多少人?21. 如图,平行四边形 , 对角线、相交于点 , , , 、是对角线上的两个动点,点从点开始向点匀速运动,点从点开始向点匀速运动,点和点同时出发,且运动速度均为 .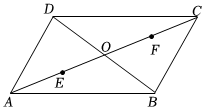 (1)、求证:当、运动过程中不与点重合时,四边形是平行四边形;(2)、若四边形为矩形,求动点、运动时间.22. 如图,是的直径,点是上一点,和过点的直线互相垂直,垂足为 , 交于点 , 且平分 .
(1)、求证:当、运动过程中不与点重合时,四边形是平行四边形;(2)、若四边形为矩形,求动点、运动时间.22. 如图,是的直径,点是上一点,和过点的直线互相垂直,垂足为 , 交于点 , 且平分 . (1)、求证:直线是的切线;(2)、连接 , 若 , , 求的长.23. 服装店销售进价为30元件的运动服,市场调查发现:当售价为50元件时,月销售量为500件;每提价1元,月销售量减少10件.若该运动服提价后的售价为元件为整数 , 月销售量为件 , 月利润元 , 请解答下列问题:(1)、直接写出与的函数关系式和自变量的取值范围;(2)、当售价为多少元时,月利润元最大,最大月利润是多少元?(3)、若商场规定运动服销量不少于300件月,且月利润不低于11250元时,求售价的取值范围.24. 如图1,在中, , , 过点作于点 , 点为线段上一点不与 , 重合 , 在线段上取点 , 使 , 连接 , .
(1)、求证:直线是的切线;(2)、连接 , 若 , , 求的长.23. 服装店销售进价为30元件的运动服,市场调查发现:当售价为50元件时,月销售量为500件;每提价1元,月销售量减少10件.若该运动服提价后的售价为元件为整数 , 月销售量为件 , 月利润元 , 请解答下列问题:(1)、直接写出与的函数关系式和自变量的取值范围;(2)、当售价为多少元时,月利润元最大,最大月利润是多少元?(3)、若商场规定运动服销量不少于300件月,且月利润不低于11250元时,求售价的取值范围.24. 如图1,在中, , , 过点作于点 , 点为线段上一点不与 , 重合 , 在线段上取点 , 使 , 连接 , . (1)、观察猜想:线段与的数量关系是 ,与的位置关系是 ;(2)、类比探究:将绕点旋转到如图2所示的位置,请写出与的数量关系及位置关系,并就图2的情形说明理由;(3)、问题解决:已知 , , 将绕点旋转,当以、、、四点为顶点的四边形为平行四边形时,直接写出的长.25. 如图1,平面直角坐标系中,抛物线交轴于 , 两点,交轴于点 , 点是线段上一个动点,过点作轴的垂线,交直线于点 , 交抛物线于点 .
(1)、观察猜想:线段与的数量关系是 ,与的位置关系是 ;(2)、类比探究:将绕点旋转到如图2所示的位置,请写出与的数量关系及位置关系,并就图2的情形说明理由;(3)、问题解决:已知 , , 将绕点旋转,当以、、、四点为顶点的四边形为平行四边形时,直接写出的长.25. 如图1,平面直角坐标系中,抛物线交轴于 , 两点,交轴于点 , 点是线段上一个动点,过点作轴的垂线,交直线于点 , 交抛物线于点 .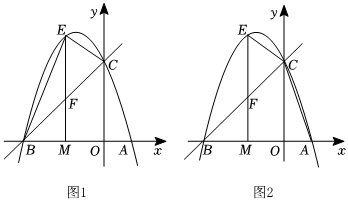 (1)、求抛物线的解析式;(2)、当面积最大时,求点的坐标;(3)、如图2,是否存在以点、、为顶点的三角形与相似,若存在,求点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当面积最大时,求点的坐标;(3)、如图2,是否存在以点、、为顶点的三角形与相似,若存在,求点的坐标;若不存在,请说明理由.