湖北省十堰市茅箭区2023年中考数学一模试卷
试卷更新日期:2023-05-15 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。)
-
1. 的绝对值是( )A、 B、11 C、 D、-112. 由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( )
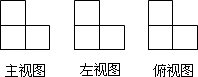 A、
A、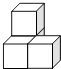 B、
B、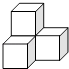 C、
C、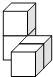 D、
D、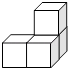 3. 下列运算中,正确的是( )A、 B、 C、 D、4. 为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
3. 下列运算中,正确的是( )A、 B、 C、 D、4. 为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.成绩/分
91
92
93
94
95
96
97
98
99
100
人数
■
■
1
2
3
5
6
8
10
12
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A、平均数,方差 B、中位数,方差 C、中位数,众数 D、平均数,众数5. 甲、乙两人每小时一共做35个电器零件,两人同时开始工作,当甲做了90个零件时乙做了120个零件,设甲每小时能做个零件,根据题意可列分式方程为( )A、 B、 C、 D、6. 函数的自变量的取值范围是( )A、 B、且 C、 D、且7. 根据图中数字的规律,若第个图中的 , 则的值为( ) A、121 B、144 C、169 D、1968. 如图,直线是的切线,为切点,交于点 , 点在上,连接 , , , 则的度数为( )
A、121 B、144 C、169 D、1968. 如图,直线是的切线,为切点,交于点 , 点在上,连接 , , , 则的度数为( ) A、 B、 C、 D、9. 如图,在中, , 点是边上一动点不与、重合 , , 交于点 , 且下列结论:当时,与全等;∽;为直角三角形时,为或;其中正确的结论有几个( )
A、 B、 C、 D、9. 如图,在中, , 点是边上一动点不与、重合 , , 交于点 , 且下列结论:当时,与全等;∽;为直角三角形时,为或;其中正确的结论有几个( ) A、1个 B、2个 C、3个 D、4个10. 如图已知反比例函数:的图象如图所示,将该曲线绕点顺时针旋转得到曲线 , 点是由曲线上一点,点在直线上,连接、 , 若 , 的面积为 , 则的值为( )
A、1个 B、2个 C、3个 D、4个10. 如图已知反比例函数:的图象如图所示,将该曲线绕点顺时针旋转得到曲线 , 点是由曲线上一点,点在直线上,连接、 , 若 , 的面积为 , 则的值为( ) A、 B、 C、-2 D、-1
A、 B、 C、-2 D、-1二、填空题(本大题共6小题,共18.0分)
-
11. 据报道,春节期间微信红包收发高达320000000次,数字320000000科学记数法表示为 .12. 不等式的解集是 .13. 小红同学在数学活动课中测量旗杆的高度,如图,已知测角仪的高度为1.58米,她在点观测旗杆顶端的仰角为 , 接着朝旗杆方向前进20米到达处,在点观测旗杆顶端的仰角为 , 则旗杆的高度为 米结果保留小数点后一位,参考数据:
 14. 如图,在矩形中, , , 点在边上, , 垂足为若 , 则线段的长为 .
14. 如图,在矩形中, , , 点在边上, , 垂足为若 , 则线段的长为 . 15. 如图,将半径为6的半圆,绕点逆时针旋转 , 使点落到点处,则图中阴影部分的面积是 .
15. 如图,将半径为6的半圆,绕点逆时针旋转 , 使点落到点处,则图中阴影部分的面积是 . 16. 如图,在中, , , , 线段绕点旋转到 , 连 , 为的中点,连接 , 则的最大值是 .
16. 如图,在中, , , , 线段绕点旋转到 , 连 , 为的中点,连接 , 则的最大值是 .
三、计算题(本大题共1小题,共5.0分)
-
17. 先化简,再求值: ,其中 .
四、解答题(本大题共8小题,共67.0分。)
-
18. 计算: .19. 已知关于的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为、 , 且 , 求的值.20. 2020年3月我国因“新冠病毒”的疫情,都不能如期开学,我市某校网上开设了“书画、器乐、戏曲、棋类”四大类兴趣课程,要求学生在家选择一项网上学习,为了解全校学生对每类课程的选择情况,随机抽取了若干名学生进行调查每人必选且只能选一类 , 先将调查结果绘制成如图两幅不完整的统计图:
 (1)、本次随机调查了多少名学生?(2)、若该校共有2000名学生,请估计全校学生选择“戏曲”类的人数.(3)、学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”,请用树状图或列表法求出恰好抽到“器乐”和“戏曲”类的概率书画、器乐、戏曲、棋类可分别用字母 , , , 表示21. 如图,在▱中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 .
(1)、本次随机调查了多少名学生?(2)、若该校共有2000名学生,请估计全校学生选择“戏曲”类的人数.(3)、学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”,请用树状图或列表法求出恰好抽到“器乐”和“戏曲”类的概率书画、器乐、戏曲、棋类可分别用字母 , , , 表示21. 如图,在▱中,对角线与相交于点 , 点 , 分别为 , 的中点,延长至 , 使 , 连接 . (1)、求证:≌;(2)、当与满足什么数量关系时,四边形是矩形?请说明理由.22. 如图,四边形内接于 , 是的直径,过点作 , 交的延长线于点 , 平分 .
(1)、求证:≌;(2)、当与满足什么数量关系时,四边形是矩形?请说明理由.22. 如图,四边形内接于 , 是的直径,过点作 , 交的延长线于点 , 平分 . (1)、求证:是的切线;(2)、已知 , , 求的半径.23. 某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系,(其中 , 且x为整数)
(1)、求证:是的切线;(2)、已知 , , 求的半径.23. 某商家正在热销一种商品,其成本为30元/件,在销售过程中发现随着售价增加,销售量在减少.商家决定当售价为60元/件时,改变销售策略,此时售价每增加1元需支付由此产生的额外费用150元.该商品销售量y(件)与售价x(元/件)满足如图所示的函数关系,(其中 , 且x为整数) (1)、直接写出y与x的函数关系式;(2)、当售价为多少时,商家所获利润最大,最大利润是多少?24. 如图 , 正方形对角线、交于点 , 、分别为正方形边、上的点,交于点 , 为中点.
(1)、直接写出y与x的函数关系式;(2)、当售价为多少时,商家所获利润最大,最大利润是多少?24. 如图 , 正方形对角线、交于点 , 、分别为正方形边、上的点,交于点 , 为中点. (1)、若 , 为中点,绕点旋转过程中,直接写出点与点的最大距离与最小距离之差.(2)、请直接写出与的数量关系.(3)、若将绕点旋转到图2所示位置时,(1)中的结论是否成立,若成立请证明;若不成立,请说明理由;25. 如图,在平面直角坐标系中,抛物线与轴的正、负半轴分别交于点、 , 与轴交于点 , 已知 , , ::4.
(1)、若 , 为中点,绕点旋转过程中,直接写出点与点的最大距离与最小距离之差.(2)、请直接写出与的数量关系.(3)、若将绕点旋转到图2所示位置时,(1)中的结论是否成立,若成立请证明;若不成立,请说明理由;25. 如图,在平面直角坐标系中,抛物线与轴的正、负半轴分别交于点、 , 与轴交于点 , 已知 , , ::4. (1)、求该抛物线的表达式;(2)、设该抛物线的对称轴分别与轴、交于点、 , 求的长;(3)、在(2)的条件下,联结 , 如果点在该抛物线的对称轴上,当和相似时,求点的坐标.
(1)、求该抛物线的表达式;(2)、设该抛物线的对称轴分别与轴、交于点、 , 求的长;(3)、在(2)的条件下,联结 , 如果点在该抛物线的对称轴上,当和相似时,求点的坐标.
-