湖北省荆州市2023年中考模拟数学试卷
试卷更新日期:2023-05-15 类型:中考模拟
一、选择题(本大题共有10个小题,每小题3分,共30分)
-
1. 若实数a的相反数为2,则a是( )A、-2 B、2 C、 D、2. 函数中自变量x的取值范围在数轴上可表示为( )A、
 B、
B、 C、
C、 D、
D、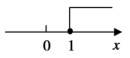 3. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,回答正确的是( )
3. 下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,回答正确的是( )已知:如图, .
求证: .
证明:延长BE交 ※ 于点F,
则 ⊙ +(三角形的外角等于与它不相邻两个内角之和).
又 , 得=____.
故( @ 相等,两直线平行).
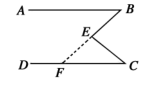 A、※代表AB B、⊙代表∠FEC C、▲代表∠EFC D、@ 代表同位角4. 下图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“楚”相对的面上的汉字是( )
A、※代表AB B、⊙代表∠FEC C、▲代表∠EFC D、@ 代表同位角4. 下图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“楚”相对的面上的汉字是( ) A、州 B、文 C、化 D、节5. 菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )A、34 B、35 C、36 D、406. 如图,一块三角形的玻璃破成三片,一位同学很快拿着其中一片玻璃说:根据所学知识就能配出一个与原三角形完全一样的图形.他这样做的依据是( )
A、州 B、文 C、化 D、节5. 菲尔兹奖是数学领域的一项国际大奖,常被视为数学界的诺贝尔奖,每四年颁发一次,最近一届获奖者获奖时的年龄(单位:岁)分别为:30,40,34,36,则这组数据的中位数是( )A、34 B、35 C、36 D、406. 如图,一块三角形的玻璃破成三片,一位同学很快拿着其中一片玻璃说:根据所学知识就能配出一个与原三角形完全一样的图形.他这样做的依据是( )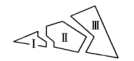 A、SSS B、SAS C、AAS D、ASA7. 我国古代数学名著《九章算术》中记载“今有共买物,人出八,盈三:人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数、物价各是多少?若设共有x人,物价是y钱,则下列方程正确的是( )A、 B、 C、 D、8. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )
A、SSS B、SAS C、AAS D、ASA7. 我国古代数学名著《九章算术》中记载“今有共买物,人出八,盈三:人出七,不足四.问人数、物价各几何?”意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问人数、物价各是多少?若设共有x人,物价是y钱,则下列方程正确的是( )A、 B、 C、 D、8. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )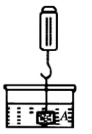 A、
A、 B、
B、 C、
C、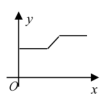 D、
D、 9.
9.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( )
 A、4 B、6 C、8 D、1010.
A、4 B、6 C、8 D、1010.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-4,-2),则点N的坐标为( )
 A、(1,-2) B、(-1,-2) C、(-1.5,-2) D、(1.5,-2)
A、(1,-2) B、(-1,-2) C、(-1.5,-2) D、(1.5,-2)二、填空题(本大题共6个小题,每小题3分,共18分)
-
11. 计算: .12. 如图,在△ABC中, , . 若点P在边AC上移动,则BP的最小值是 .
 13. 若一元二次方程满足且有两个相等实数根,则a与c的关系是 .14. 有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是 .15. 如图,某校数学兴趣小组的同学测量校园内一棵树DE的高度,他们在这棵树的正前方一旗台的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度 , 台阶AC的坡度为 , 且B,C,E三点在同一直线上,则树高DE为m.(测倾器的高度忽略不计)
13. 若一元二次方程满足且有两个相等实数根,则a与c的关系是 .14. 有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形都既是轴对称图形,又是中心对称图形的概率是 .15. 如图,某校数学兴趣小组的同学测量校园内一棵树DE的高度,他们在这棵树的正前方一旗台的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度 , 台阶AC的坡度为 , 且B,C,E三点在同一直线上,则树高DE为m.(测倾器的高度忽略不计) 16. 如图,A(4,3)是反比例函数在第一象限图象上一点,连接OA,过A作轴,截取(B在A上方),连接OB,交反比例函数的图象于点C.则点C的坐标是 .
16. 如图,A(4,3)是反比例函数在第一象限图象上一点,连接OA,过A作轴,截取(B在A上方),连接OB,交反比例函数的图象于点C.则点C的坐标是 .
三、解答题(本大题共有8个小题,共72分,)
-
17. 已知x,y满足方程组求代数式的值.18. 已知: , 先化简A,再从不等式组的解集中取一个合适的值代入,求A的值.19. 如下图,在四边形ABCD中, , E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且 , 连接EG,试确定EG与DF的位置关系,并说明理由.
 20. 某中学为了提高学生的综合素质,成立了以下社团:A-机器人,B-围棋,C-羽毛球,D-电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.
20. 某中学为了提高学生的综合素质,成立了以下社团:A-机器人,B-围棋,C-羽毛球,D-电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图.根据以上信息,解答下列问题:
 (1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完整;(3)、若该校共有1000名学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团.21. 如图,以菱形ABCD的边AB为直径的⊙O交对角线AC于点P,过P作PE⊥BC,垂足为E.
(1)、这次被调查的学生共有人;(2)、请你将条形统计图补充完整;(3)、若该校共有1000名学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团.21. 如图,以菱形ABCD的边AB为直径的⊙O交对角线AC于点P,过P作PE⊥BC,垂足为E.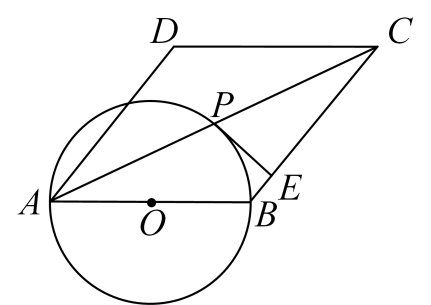 (1)、求证:PE是⊙O的切线;(2)、若菱形ABCD的面积为24, , 求PE的长.22. 随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机,某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%.(1)、求A型自行车去年每辆售价多少元?(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?23. 阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
(1)、求证:PE是⊙O的切线;(2)、若菱形ABCD的面积为24, , 求PE的长.22. 随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机,某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%.(1)、求A型自行车去年每辆售价多少元?(2)、该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍已知A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?23. 阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点. (1)、【解决问题】
(1)、【解决问题】
如图1, , 试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)、如图2,在矩形ABCD中, , , 且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E,并连接DE,CE;(3)、【拓展探究】
如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.24. 如图,抛物线与x轴交于A(-3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作交x轴于点E,交BC于点F. (1)、求抛物线的解析式:(2)、试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)、请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.
(1)、求抛物线的解析式:(2)、试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;(3)、请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.