湖北省恩施市2023年中考一模数学试卷
试卷更新日期:2023-05-15 类型:中考模拟
一、单选题
-
1. 的相反数等于( )A、 B、2023 C、 D、2. 如图几种著名的数学曲线中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 函数y= 中,自变量x的取值范围是( )A、x>0 B、x>1 C、x>0且x≠1 D、x≥0且x≠14. 一个正方体的表面展开图如图所示,把它折成正方体后,与“山”字相对的字是( )
3. 函数y= 中,自变量x的取值范围是( )A、x>0 B、x>1 C、x>0且x≠1 D、x≥0且x≠14. 一个正方体的表面展开图如图所示,把它折成正方体后,与“山”字相对的字是( )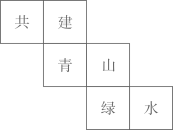 A、水 B、绿 C、建 D、共5. 下列运算正确的是( )A、 B、 C、 D、6. 某校航模兴趣小组共有50位同学,他们的年龄分布如表:
A、水 B、绿 C、建 D、共5. 下列运算正确的是( )A、 B、 C、 D、6. 某校航模兴趣小组共有50位同学,他们的年龄分布如表:年龄/岁
13
14
15
16
人数
5
23
▃
▃
由于表格污损,15和16岁人数不清,则下列关于年龄的统计量可以确定的是( )
A、平均数、众数 B、众数、中位数 C、平均数、方差 D、中位数、方差7. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=45°,那么∠BAF的大小为( ) A、15° B、10° C、20° D、25°8. 杨辉是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家.他与秦九韶、李冶、朱世杰并称“宋元数学四大家”.他所著《田亩比类乘除算法》( 年)提出的这样一个问题:“直田积(矩形面积)八百六十四步(平方步),阔(宽)不及长一十二步(宽比长少一十二步)﹒问阔及长各几步.”若设阔为 步,则可列方程( )A、 B、 C、 D、9. 如图,在中, , 以点C为圆心,长为半径画弧,交于点B和D,分别以点B,D为圆心,大于长为半径画弧,两弧交于点M,作射线交AB于点E,若 , 则的长度为( )
A、15° B、10° C、20° D、25°8. 杨辉是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家.他与秦九韶、李冶、朱世杰并称“宋元数学四大家”.他所著《田亩比类乘除算法》( 年)提出的这样一个问题:“直田积(矩形面积)八百六十四步(平方步),阔(宽)不及长一十二步(宽比长少一十二步)﹒问阔及长各几步.”若设阔为 步,则可列方程( )A、 B、 C、 D、9. 如图,在中, , 以点C为圆心,长为半径画弧,交于点B和D,分别以点B,D为圆心,大于长为半径画弧,两弧交于点M,作射线交AB于点E,若 , 则的长度为( ) A、3 B、 C、 D、210. 如图,在直角三角形中, , , , 点M是边上一点(不与点A,B重合),作于点E,于点F,则的最小值是( )
A、3 B、 C、 D、210. 如图,在直角三角形中, , , , 点M是边上一点(不与点A,B重合),作于点E,于点F,则的最小值是( ) A、2 B、2.4 C、2.5 D、2.611. 如图,已知 中, , ,点 为 的中点,点 在线段 上以 的速度由 点向 点运动,同时,点 在线段 上以相同速度由点 向点A运动,一个到达终点后另一个点也停止运动,当 与 全等时,点 运动的时间是( )
A、2 B、2.4 C、2.5 D、2.611. 如图,已知 中, , ,点 为 的中点,点 在线段 上以 的速度由 点向 点运动,同时,点 在线段 上以相同速度由点 向点A运动,一个到达终点后另一个点也停止运动,当 与 全等时,点 运动的时间是( ) A、 B、 C、 D、 或12. 抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=-2,过点(1,-2)和点(x0 , y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a-2b;③16a+c>4b;④若 >-4,则 >c.其中正确结论的个数为( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、 或12. 抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=-2,过点(1,-2)和点(x0 , y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a-2b;③16a+c>4b;④若 >-4,则 >c.其中正确结论的个数为( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 13的算术平方根是 .14. 分解因式: .15. 如图, 内切于 ,切点分别为 、 、 ,若 , , ,则图中阴影部分的面积是 .
 16. 对于正数 ,规定 ,例如: , , , …利用以上的规律计算: .
16. 对于正数 ,规定 ,例如: , , , …利用以上的规律计算: .三、解答题
-
17. 先化简,再求值: , 其中.18. 如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
 19. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
19. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图: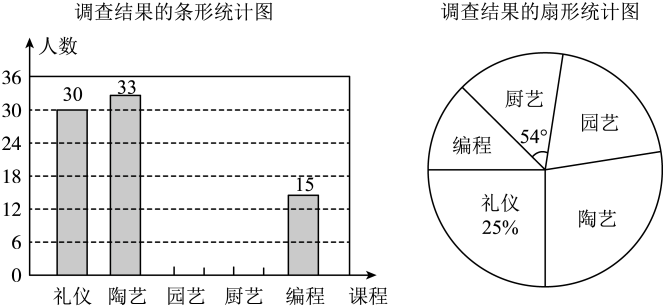
请结合上述信息,解答下列问题:
(1)、共有名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是度;(2)、补全调查结果条形统计图;(3)、小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.20. 如图,一艘轮船从点处以的速度向正东方向航行,在处测得灯塔在北偏东方向上,继续航行到达处,这时测得灯塔在北偏东方向上,已知在灯塔的四周内有暗礁,问这艘轮船继续向正东方向航行是否安全?并说明理由.(提示: , )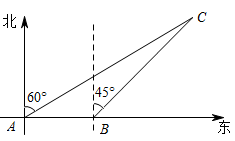 21. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .
21. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、两点,与双曲线交于点、两点, .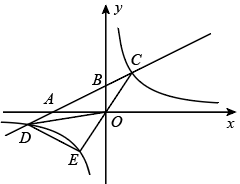 (1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.22. 在建设美好乡村活动中,某村民委员会准备在乡村道路两旁种植柏树和杉树.经市场调查发现:购买2棵柏树和3棵杉树共需440元,购买3棵柏树和1 棵杉树共需380元.(1)、求柏树和杉树的单价;(2)、若本次美化乡村道路臀购买柏树和杉树共150棵(两种树都必须购买),且柏树的棵数不少于树的3倍,设本次活动中购买柏树x棵,此次购树的费用为w元.
(1)、求 , 的值;(2)、求点坐标并直接写出不等式的解集;(3)、连接并延长交双曲线于点 , 连接、 , 求的面积.22. 在建设美好乡村活动中,某村民委员会准备在乡村道路两旁种植柏树和杉树.经市场调查发现:购买2棵柏树和3棵杉树共需440元,购买3棵柏树和1 棵杉树共需380元.(1)、求柏树和杉树的单价;(2)、若本次美化乡村道路臀购买柏树和杉树共150棵(两种树都必须购买),且柏树的棵数不少于树的3倍,设本次活动中购买柏树x棵,此次购树的费用为w元.①求w与x之间的函数表达式,并写出x的取值范围?
②要使此次购树费用最少,柏树和杉树各需购买多少棵?最少费用为多少元?

