湖北省鄂州市2023年中考4月学业质量监测数学试题

试卷更新日期：2023-05-15 类型：中考模拟

进入出卷网下载

一、选择题(本大题共10小题,每小题3分,共计30分)

1. 实数2的相反数等于（）

A、-2 B、+2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $α^{3} \cdot α^{4} = α^{12}$ C、 ${(a^{3})}^{4} = a^{12}$ D、 $(a b)^{2} = a b^{2}$

查看试题解析
3. 2022年3月，国务院总理李克强在政府工作报告中指出：2021年，我国经济保持恢复发·展，国内生产总值达到1140000亿元.将1140000用科学记数法表示应为（）.

A、 $0.114 \times 1 0^{7}$ B、 $1.14 \times 1 0^{7}$ C、 $1.14 \times 1 0^{6}$ D、 $11.4 \times 1 0^{5}$

查看试题解析
4. 下列几何体中，主视图是圆的是( ）

A、 B、 C、 D、

查看试题解析
5. 如图，直线 $A B / / C D ， D E ⊥ B C$ 于点 $E$ ，若 $∠ C D E = 5 7^{°}$ ，则 $∠ 1$ 的度数是 $(⋯)$

A、 $5 7^{°}$ B、 $3 3^{°}$ C、 $2 3^{°}$ D、 $4 7^{°}$

查看试题解析
6. 已知不等式组 ${\begin{array}{l} 2 x - a < 1 \\ x - 2 b > 3 \end{array}$ 的解集是 $- 1 < x < 1$ ，则 $(a + 1) (b + 1)$ 的值是的（）

A、-2 B、4 C、2 D、-4

查看试题解析
7. 如图，A(0，1)，M(3，2)，N(5，5).点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线L：y=-x+b也随之平行移动，设移动时间为t秒，当M，N位于直线l的异侧时，t应该满足的条件是（）

A、 $3 < t < 6$ B、 $4 < t < 9$ C、 $3 < t < 7$ D、 $\sqrt{5} < t < 7$

查看试题解析
8. 如图，以等边△ABC的一边AB为直径的半圆О交AC于点D，交BC于点E，若.AB=4，则阴影部分的面积是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、 $2 \sqrt{5}$

查看试题解析
9. 抛物线y²=ax+bx+c(a≠0)的对称轴是直线x.=-1，且过点(1，0)，顶点位于第二象限，其部分图象如图所示，给出以下判断：①ab>0且c<0；②4a-2b+c>0；③8a+c>0；c=3a-36.其中错误的选项是（）

A、①③ B、①③④ C、②④ D、②③④

查看试题解析
10. 如图，边长为α的等边△ABC中，BF是AC.上中线，点D是线段：BF上的动点，连接AD，在AD的右侧作等边△ADE，连接BE，则AE+BE的最小值是（）

A、 $(\sqrt{3} + 1) a$ B、 $3 a - 1$ C、 $\sqrt{5} a$ D、 $\sqrt{3} a$

查看试题解析

二、填空题(本大题共6小题,每小题3分,共计18分)

11. 计算： $- \sqrt{4}$ =

查看试题解析
12. 为了落实“双减”，增强学生体质，阳光学校篮球兴趣小组开展投篮比赛活动.6名选手投中篮圈的个数分别为6，9，9，10，9，8，则这组数据的众数是.

查看试题解析
13. 若实数a、b分别满足 $a^{2} - 4 a + 2 = 0 ， b^{2} - 4 b + 2 = 0$ ，且 $a \neq b$ ，则 $\frac{1}{a} + \frac{1}{b}$ 的值为.

查看试题解析
14. 如图，在平面直角坐标系中，已知A(1，0)，B(2，1)，D(3，0)，△ABC与△DEF位似，原点О是位似中心，则E点的坐标是。

查看试题解析
15. 如图，直线AB：y=2x+4与双曲线y= $\frac{6}{x}$ 交于A(1，6)，B(-3，-2)两点，直线BO与双曲线在第一象限交于点C，连接AC.则 $S_{△ A B C}$ =

查看试题解析
16. 如图，在矩形ABCD中，点E在边AB上，ABEC与AFEC关于直线EC对称，点B的对称点F在边AD上，G为CD中点，连结BG分别与CE；CF交于M，N两点，若BM=BE，MG=1，则线段BM的值为.

查看试题解析

三、解答题(本大题共8小题,17~21题每题8分,22~23题每题10分,24题12分,共计

17. 先化简，再求值： $\frac{a^{2}}{a - 1} - \frac{1}{a - 1}$ ，其中 $a = 3$ .

查看试题解析
18. 如图，DB是平行四边形ABCD的对角线：

(1)、尺规作图(请用2B铅笔)：作线段BD的垂直平分线EF，交AB，DB、DC分别于E，O，F，连接DE、BF(保留作图痕迹，不写作法)

(2)、试判断四边形DEBF的形状，并说明理由..

查看试题解析

19. 为了加强学生的垃圾分类意识；某校进行了一次系统全面的垃圾分类宣传.为了解这次宣传的效果，从全校学生中随机抽取部分学生进行了一次测试，测试结果共分为四个等级：A.优秀；B.良好；C.及格；D.不及格.根据调查统计结果，绘制了如图所示的不完整的统计表：
垃圾分类知识测试成绩统计表

测试等级	百分比	又数
A.优秀	5%	20
B.良好		60
C.及格	45%	m
D.不及格	n

请结合统计表，回答下列问题：

(1)、求m、n的值；

(2)、如果测试结果为“良好”及以上即为对垃圾分类知识比较了解，已知该校学生总数为5600人，请根据本次抽样调查的数据估计全校比较了解垃圾分类知识的学生人数；

(3)、为了进一步在学生中普及垃圾分类知识，学校准备再开展一次关于垃圾分类的知识竞赛，要求每班派一人参加：某班要从在这次测试成绩为优秀的小明和小亮中选一人参加.班长设计了如下游戏来确定人选，具体规则：把四个完全相同的乒乓球分别标上数字1，2，3，4，然后放到一个不透明的袋中充分摇匀，两人同时：.从袋中各摸出一个球，若摸出的两个球上的数字和为奇数，则小明参加，否则小亮参加.请用树状图或列表法说明这个游戏规则是否公平.

查看试题解析

20. 图20-1是某型号挖掘机，该挖掘机是由基座、主臂和伸展臂构成.图20-2是其侧面结构示意图(MN是基座的高，MP是主臂，PQ是伸展臂).已知基座高度MN为0.5米，主臂MP长为 $3 \sqrt{2}$ 米，主臂伸展角α的范围是：0°<a≤60°，伸展臂伸展角β的·范围是：45°≤p≤135°.当α=45°时(如图20-3)，伸展臂PQ恰好垂直并接触地面.

(1)、求伸展臂PQ长为多少米；

(2)、挖掘机能挖的最远处距点Ⅳ的距离QN为多少米.

查看试题解析
21. 有A、B、C三家工厂依次坐落在一条笔直的公路边，甲、乙两辆运货卡车分别从A、B工厂同时出发，沿公路匀速驶向C工厂，最终到达C工厂.设甲、乙两辆卡车行驶x(h)后，与B工广的距离分别为y₁_、y₂(km)，y₁_、y₂与x的函数关系如图所示，根据图象解答下列问题.(提示：图中较粗的折线表示的是y与x的函数关系.)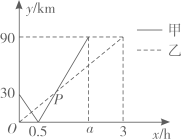

(1)、A、C两家工厂之间的距离为km，

(2)、a= ， P点坐标是

(3)、求甲，乙两车之间的距离不超过10km时x的取值范围.

查看试题解析
22. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形， $∠ B A C = 7 5^{°} ， ∠ A B C = 4 5^{°}$ .连接AO并延长，交 $⊙ O$ 于点 $D$ ，连接BD.过点 $C$ 作 $⊙ O$ 的切线，与BA的延长线相交于点 $E$ .

(1)、求证： $A D / / E C$ .

(2)、若 $A B = 12$ ，求 $S_{△ A C E}$ .

查看试题解析
23. 如图

(1)、【特例感知】如图23-1，对于抛物线 $y_{1} = - x^{2} - x + 1 ， y_{2} = - x^{2} - 2 x + 1 ， y_{3} = - x^{2} - 3 x + 1$ ，下列结论正确的序号是
①抛物线 $y_{1} ， y_{2} ， y_{3}$ 都经过点 $C (0 ， 1)$ ；

②抛物线 $y_{2} ， y_{3}$ 的对称轴由拋物线 $y_{1}$ 的对称轴依次向左平移 $\frac{1}{2}$ 个单位得到；

③抛物线 $y_{1} ， y_{2} ， y_{3}$ 与直线 $y = 1$ 的交点中，相邻两点之间的距离相等.

(2)、
【形成概念】把满足 $y_{n} = - x^{2} - n x + 1$ ( $n$ 为正整数)的抛物线称为“系列平移抛物线”.
【知识应用】在(2)中，如图 $23 - 2$ .
①“系列平移抛物线”的顶点依次为 $P_{1} ， P_{2} ， P_{3} ， ⋯ ， P_{n}$ ，用含n的代数式表示顶点P_n的坐标，并写出该顶点纵坐标y与横坐标x之间的关系式；

②“系列平移拔物线”存在“系列整数点(横、纵坐标均为整数的点)”： $C_{1}$ ， $C_{2} ， C_{3} ， ⋯ ， C_{n}$ ，其横坐标分别为： $- k - 1 ， - k - 2 ， - k - 3 ， ⋯ ， - k - n (k$ 为正整数)，判断相邻两点之间的距离是否都相等，若相等，请求出相邻两点之间的距离；若不相等，说明理由.

③在②中，直线 $y = 1$ 分别交“系列平移抛物线”于点 $A_{1} ， A_{2} ， A_{3} ⋯ A_{n}$ ，连接 $C_{n} A_{n} ， C_{n - 1} A_{n - 1}$ ，判断直线 $C_{n} A_{n} ， C_{n - 1} A_{n - 1}$ 是否平行?请直接写出判断结果.

查看试题解析
24. 在平面直角坐标系中，已知顶点为 $P$ 的抛物线 $C_{1}$ 的解析式是 $y = a (x - 3)^{2} (a > 0)$ ，且经过点 $(0 ， 1)$ .

(1)、求 $a$ 的值；

(2)、如图 $24 - 1$ ，将抛物线 $C_{1}$ 向下平移 $h (h > 0)$ 个单位长度得到抛物线 $C_{2}$ ，过点 $M (0 ， m^{2}) (m > 0)$ 作直线 $l$ 平行于 $x$ 轴，与两抛物线从左到右分别相交于A、B、C、D四点，且A、C两点关于 $y$ 轴对称.
①点 $G$ 在抛物线 $C_{1}$ 上，当点 $C$ 的坐标为何值时，四边形APCG是平行四边形?

②如图24-2，若抛物线 $C_{r}$ 的对称轴与抛物线 $C_{2}$ 交于点 $Q$ ，试探究：在 $M$ 点的运动过程中， $\frac{A C}{P Q}$ 的比值是否为一个定值；如果是，请求出此定值；如果不是，请说明理由.

查看试题解析