2023年中考数学复习考点一遍过——三角形全等/相似

试卷更新日期：2023-05-15 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列各组中的两个三角形一定全等的是（）

A、以100°为内角，10厘米为一边长的两个等腰三角形 B、斜边相等的两个直角三角形 C、有一边相等的两个等腰直角三角形 D、以4，9为边的两个等腰三角形

查看试题解析
2. 下列四个命题中，原命题和逆命题都是真命题的是（）

A、全等三角形的对应角都相等 B、如果两个实数相等，那么这两个实数的平方相等 C、对顶角相等 D、等边三角形每一个角都等于60°

查看试题解析
3. 下列说法不正确的是（）

A、如果两个图形全等，那么它们的形状和大小一定相同； B、面积相等的两个图形是全等图形； C、图形全等，只与形状、大小有关，而与它们的位置无关； D、全等三角形的对应边相等，对应角相等；

查看试题解析
4. 下列说法正确的是（）

A、全等图形是指形状相同的两个图形 B、全等图形的周长和面积一定相等 C、两个等边三角形一定全等 D、面积相等的两个三角形一定全等

查看试题解析
5. 下列说法正确的是（　　）

A、所有的等腰三角形都相似 B、有一对锐角相等的两个三角形相似 C、相似三角形都是全等的 D、所有的等边三角形都相似

查看试题解析
6. 下列各组所述几何图形中，一定全等的是（　　）

A、一个角是 $45^{\circ}$ 的两个等腰三角形 B、两个等边三角形 C、各有一个角是 $40^{\circ}$ ，腰长都是8cm的两个等腰三角形 D、腰长相等的两个等腰直角三角形

查看试题解析
7. 下列说法错误的是（　　）

A、全等三角形的对应边相等 B、全等三角形的角相等 C、全等三角形的周长相等 D、全等三角形的面积相等

查看试题解析
8. 下列结论不正确的是（　　）

A、两个锐角对应相等的两个直角三角形全等 B、一锐角和斜边对应相等的两个直角三角形角形全等 C、一直角边和一锐角对应相等的两个直角三角形全等 D、两条直角边对应相等的两个直角三角形全等

查看试题解析
9. 下列语句中，不正确的是（　　）

A、两条直角边相等的两个直角三角形全等 B、锐角三角形中，两边及第三边上的高对应相等的两个三角形全等 C、两边及其中一边上的高对应相等的两个三角形全等 D、两个锐角对应相等的两个直角三角形全等

查看试题解析
10. 如图所示，E是正方形 $A B C D$ 的对角线 $B D$ 上一点， $E F ⊥ B C$ ， $E G ⊥ C D$ ，垂足分别是F、G，若 $C G = 4$ ， $C F = 3$ ，则 $A E$ 的长是（）

A、3 B、4 C、5 D、7

查看试题解析

二、填空题（每空3分，共15分）

11. 如图，矩形 $A B C D$ ，点E为 $A B$ 上一点，连接 $C E$ ，在 $C E$ 上取一点F，连接 $B F$ ，过F作 $C E$ 的垂线交 $A D$ 于点H，若 $∠ E B F + ∠ B C E = 90 °$ ， $C E = 2 F H$ ， $A D = 6$ ， $C E = 2 \sqrt{10}$ ，则 $C D$ 的长是．

查看试题解析
12. 三个全等三角形摆成如图所示的形式，则 $∠ α + ∠ β + ∠ γ$ 的度数为.

查看试题解析
13. 如图，平行四边形ABCD，点F是BC上的一点，∠FAD=60°，AE平分∠FAD，交CD于点E，且点E是CD的中点，连接EF，已知AD=5，CF=3，则EF=

查看试题解析
14. 如图，在 ▱ ABCD，点F是BC上的一点，连接AF，AE平分∠FAD，交CD于中点E，连接EF．若∠FAD＝60°，AD＝5，CF＝3，则EF＝．

查看试题解析
15. 如图，在等腰 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 2$ ， D为 $B C$ 边的中点，过点C作 $C E ⊥ A D$ 于点E，交 $A B$ 于点F，则线段 $B F$ 的长为.

查看试题解析

三、解答题（共8题，共75分）

16. 如图，点D为 $△ A B C$ 的边 $A B$ 的中点，过点D作 $D E ∥ B C$ ，交 $A C$ 于点E，延长 $D E$ 至点F，使 $D E = E F$ ，求证： $△ C F E ∽ △ A B C$ .

查看试题解析
17. 如图，已知四边形ABCD是平行四边形，点E，F分别是AB，BC上的点，AE=CF，并且∠AED=∠CFD．

求证：

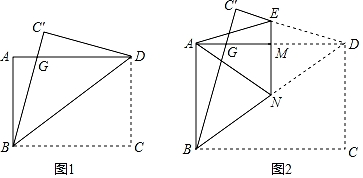
(1)、△AED≌△CFD；

(2)、四边形ABCD是菱形．

查看试题解析
18. 如图， $A B = A C$ ， $C E ∥ A B$ ， D是 $A C$ 上的一点，且 $A D = C E$ .

(1)、求证： $△ A B D ≌ △ C A E$

(2)、若 $∠ A B D = 25 °$ ， $∠ C B D = 40 °$ ，求 $∠ B A E$ 的度数.

查看试题解析
19. 如图1，四边形ABCD为正方形，点M是对角线BD上的一点(0<BM< $\frac{1}{2}$ BD)，连接AM，过点M作MN．⊥AM交CD于点N．

(1)、求证：AM=MN．

(2)、如图2，以MA，MN为邻边作矩形AMNP，连接PD．
①求证：BM= PD；

②若正方形ABCD的边长为 $6 \sqrt{2}$ ， PD=4，求AM的长．

查看试题解析
20. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，过点 $A$ 作 $A E ⊥ B D$ 于点 $E$ ，过点 $C$ 作 $C F ⊥ B D$ 于点 $F$ .

(1)、求证： $△ A O E$ ≌ $△ C O F$ ；

(2)、若 $A E = O E$ ，求 $∠ B A E$ 的度数.

查看试题解析
21. 如图，在矩形 $A B C D$ 中，点E，O分别为 $B C ， B D$ 的中点，过点A作 $A F ∥ B D$ 交EO的延长线于点F，连接 $C F$ 交 $B D$ 于点G.

(1)、求证：四边形 $A B O F$ 为平行四边形.

(2)、若 $C F ⊥ B D$ ，且 $A B = 6$ ，求 $O G$ 的长.

查看试题解析
22. 如图，E、F是▱ABCD的对角线AC上的两点，且BE⊥AC，DF⊥AC，连接ED，FB.

(1)、求证：AE=CF．

(2)、连接BD交AC于点O，若BE＝4，EF＝6，求BD的长．

查看试题解析
23. 如图1，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD折叠，点C落在点C′的位置，BC′交AD于点G.

(1)、求证：BG＝DG；

(2)、求C′G的长；

(3)、如图2，再折叠一次，使点D与A重合，折痕EN交AD于M，求EM的长.

查看试题解析