北师大版2022-2023学年度第二学期七年级数学 利用三角形全等测距离 期末复习
试卷更新日期：2023-05-15 类型：复习试卷
一、单选题
-
1. 如图，要测量河两岸相对的两点A、B的距离，先在河岸BF上取两点C、D，使CD＝BC，再作DE⊥BF，垂足为D，使A、C、E三点在一条直线上，测得ED＝30米，因此AB的长是（ ）
A、10米 B、20米 C、30米 D、40米2. 如图，有一池塘，要测池塘两端A，B的距离，可先在平地上取一个直接到达A和B的点C，连接AC并延长到D，使CD＝CA，连接BC并延长到E，使CE＝CB，连接DE，那么量出DE的长，就是A、B的距离.我们可以证明出△ABC≌△DEC，进而得出AB＝DE，那么判定△ABC和△DEC全等的依据是（ ）
A、SSS B、SAS C、ASA D、AAS3. 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离到达C点.然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点.那么C，D两点间的距离就是在A点处小明与游艇的距离.在这个问题中，可作为证明的依据的是（ ）
A、或 B、或 C、或 D、或4. 根据下列已知条件，能作出唯一△ABC的是（ ）A、AB＝3，BC＝4，CA＝8 B、AB＝4，BC＝3，∠A＝60° C、∠A＝60°，∠B＝45°，AB＝4 D、∠C＝90°，∠B＝30°，∠A＝60°5. 如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④BE=DE；⑤S△BDE：S△ACD=BD：AC，其中正确的个数（ ）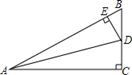
A、5个 B、4个 C、3个 D、2个6. 如图，把两根钢条AB，CD的中点O连在一起，可以做成一个测量工件内槽宽的工具（卡钳）．只要量得AC之间的距离，就可知工件的内径BD．其数学原理是利用△AOC≌△BOD，判断△AOC≌△BOD的依据是（ ）
A、SAS B、SSS C、ASA D、AAS7. 小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第_____块去，这利用了三角形全等中的_____原理（ ）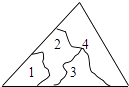
A、2；SAS B、4；ASA C、2；AAS D、4；SAS8. 如图，红红书上的三角形被墨迹污染了一部分，她根据所学的知识很快就画了一个与书上完全一样的三角形，那么红红画图的依据是（ ）
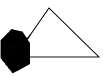A、SSS B、SAS C、ASA D、AAS9. 小明沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙0点，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息如下：如图，AB∥OE，OE∥CD，AC与BD相交于点O，OD⊥CD，垂足为点D，下列结论中不正确的是（ ）
A、∠BOA=∠DOC B、AB∥CD C、∠ABD=90° D、与∠AOE相等的角共有2个10. 山西中学阶段考试要求提出继续加大考查“活动建议”力度，目的是考查学生运用所学知识解决问题的能力，体现实践创新．某实践活动小组成员要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在同一条直线上，如图，可以得到△EDC≌△ABC，所以ED=AB，因此测得ED的长就是AB的长，判定△EDC≌△ABC的理由是（ ）
A、SAS B、ASA C、SSS D、AAS二、填空题
-
11. 如图，小强站在河边的点处，在河的对面（小强的正北方向）的处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了20步到达一棵树处，接着再向前走了20步到达处，然后他左转直行，当小强看到电线塔、树在一条直线时（即电线塔、树与自己现处的位置在一条直线上），他一共走了90步．如果小刚一步大约50厘米，估计小刚在点处时他与电线塔的距离为米．
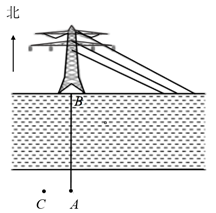12. 如图，小明站在堤岸的A点处，正对他的S点停有一艘游艇.他想知道这艘游艇距离他有多远，于是他沿堤岸走到电线杆B旁，接着再往前走相同的距离，到达C点.然后他向左直行，当看到电线杆与游艇在一条直线上时停下来，此时他位于D点.小明测得C、D间的距离为90米，则在A点处小明与游艇的距离为米.
13. 如图，小明与小敏玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小敏从水平位置CD下降40cm时，这时小明离地面的高度是 ．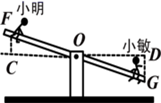
14. 如图，是一个3×3的正方形网格，则∠1+∠2+∠3+∠4=。
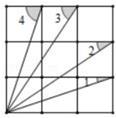15. 如图，在等腰 中， ，点 是 内一点，且 ．联结 并延长，交边 于点 ．如果 ，那么 的值为 ．
三、解答题
-
16. 如图是一个工业开发区局部的设计图，河的同一侧有两个工厂A和B，AD、BC的长表示两个工厂到河岸的距离，其中E是进水口，D、C为两个排污口．已知AE＝BE，∠AEB＝90°，AD⊥DC，BC⊥DC，点D、E、C在同一直线上，AD＝150米，BC＝350米，求两个排污口之间的水平距离DC．
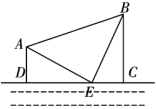17. 在学习完“探索三角形全等的条件”一节后，小丽总结出很多全等三角形的模型，她设计了以下问题给同桌解决：如图，做一个“U”字形框架PABQ，AP，BQ足够长，PA⊥AB于点A，QB⊥AB于点B，她在框架里放了两根长度相等的木条CM、NM，且CM⊥MN，点C、M、N分别在PA、AB、BQ上，若AM＝4cm，求BN的长．
18. 如图1，油纸伞是中国传统工艺品之一，起源于中国的一种纸制或布制伞．油纸伞的制作工艺十分巧妙，如图2，伞圈D沿着伞柄AP滑动时，总有伞骨 ， ，从而使得伞柄AP始终平分同一平面内两条伞骨所成的 ．请你说明其中的理由．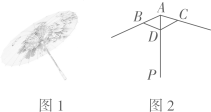
四、综合题
-
19. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC=BC，∠ACB=90°），点C在DE上，点A和B分别与木墙的顶端重合。
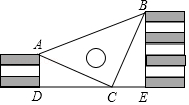(1)、求证：△ADC≌△CEB；(2)、求两堵木墙之间的距离。20. 如图：小刚站在河边的A点处，在河的对面（小刚的正北方向）的B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了20步到达一棵树C处，接着再向前走了20步到达D处，然后他左转90°直行，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他共走了100步．
(1)、根据题意，画出示意图；(2)、如果小刚一步大约50厘米，估计小刚在点A处时他与电线塔的距离，并说明理由．21. 如图1，已知 ， 是等边三角形，点 为射线 上任意一点（点 与点 不重合），连结 ，将线段 绕点 逆时针旋转 得到线段 ，连结 并延长交射线 于点 ．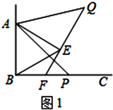
(1)、如图1，当 时， ，猜想 ；(2)、如图2，当点 为射线 上任意一点时，猜想 的度数，并说明理由；22. 如图，点B，F，C，E在直线l上（点F，点C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC．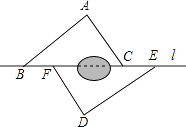
(1)、求证：△ABC≌△DEF；(2)、指出图中所有平行的线段，并说明理由．23.(1)、探索发现：如图1，在 中，点 在边 上， 与 的面积分别记为 与 ，试判断 与 的数量关系，并说明理由．
(2)、阅读分析：小鹏遇到这样一个问题：如图，在 中， ， ，射线 交 于点 ，点 、 在 上，且 ，试判断 、 、 三条线段之间的数量关系．小鹏利用一对全等三角形，经过推理使问题得以解决．图2中的 、 、 三条线段之间的数量关系为 ， 并说明理由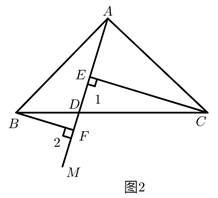
(3)、类比探究：如图3，在四边形 中， ， 与 交于点 ，点 、 在射线 上，且 ．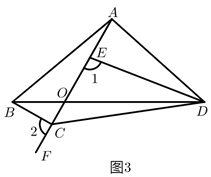
①全等的两个三角形为；
②若 ， 的面积为2，直接写出 的面积： ．