北师大版2022-2023学年度第二学期七年级数学 用尺规作三角形 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( )
 A、4个 B、3个 C、2个 D、1个2. 已知下列条件,不能作出唯一三角形的是( )A、两边及其夹角 B、两角及其夹边 C、三边 D、两边及除夹角外的另一个角3. 已知线段a、b和m,求作△ABC,使BC=a,AC=b,BC上的中线AD=m,作法的合理顺序为( )
A、4个 B、3个 C、2个 D、1个2. 已知下列条件,不能作出唯一三角形的是( )A、两边及其夹角 B、两角及其夹边 C、三边 D、两边及除夹角外的另一个角3. 已知线段a、b和m,求作△ABC,使BC=a,AC=b,BC上的中线AD=m,作法的合理顺序为( )
①延长CD到B,使BD=CD;②连结AB;③作△ADC,使DC=a,AC=b,AD=m
A、③①② B、①②③ C、②③① D、③②①4. 数学活动课上,老师在黑板上画直线平行于射线AN(如图),让同学们在直线l和射线AN上各找一点B和C , 使得以A、B、C为顶点的三角形是等腰直角三角形.这样的三角形最多能画( )个.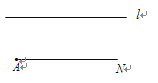 A、1 B、2 C、3 D、45. 已知三边作三角形,用到的基本作图是( )
A、1 B、2 C、3 D、45. 已知三边作三角形,用到的基本作图是( )
A、作一个角等于已知角 B、平分一个已知角 C、在射线上截取一线段等于已知线段 D、作一条直线的垂线6. 如图的中, , 且为上一点.今打算在上找一点 , 在上找一点 , 使得与全等,以下是甲、乙两人的作法:甲连接 , 作的中垂线分别交、于点、点,则、两点即为所求
乙过作与平行的直线交于点,过作与平行的直线交于点,则、两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确7. 根据下列已知条件,能唯一画出△ABC的是( )A、AB=3,BC=4,AC=8 B、∠C=90°,AB=6 C、AB=3,BC=3,∠C=30° D、∠A=60°,∠B=45°,AB=48. 如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是( )
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确7. 根据下列已知条件,能唯一画出△ABC的是( )A、AB=3,BC=4,AC=8 B、∠C=90°,AB=6 C、AB=3,BC=3,∠C=30° D、∠A=60°,∠B=45°,AB=48. 如图,已知一条线段的长度为a,作边长为a的等边三角形的方法是:①画射线AM;②连结AC、BC;③分别以A、B为圆心,以a的长为半径作圆弧,两弧交于点C;④在射线AM上截取AB=a;以上画法正确的顺序是( )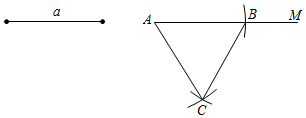 A、①②③④ B、①④③② C、①④②③ D、②①④③9. 如图,在5 5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,若画出以AB为腰的等腰三角形ABC,使得点C在格点上,则点C的个数是( )
A、①②③④ B、①④③② C、①④②③ D、②①④③9. 如图,在5 5的正方形网格中,每个小正方形的边长均为1,线段AB的端点在格点上,若画出以AB为腰的等腰三角形ABC,使得点C在格点上,则点C的个数是( ) A、3个 B、4个 C、5个 D、6个10. 如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A、3个 B、4个 C、5个 D、6个10. 如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )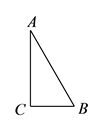 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在正方形方格中,各正方形的顶点叫做格点,三个顶点都在格点上的三角形称为格点三角形。图中 是格点三角形,请你找出方格中所有与 全等,且以A为顶点的格点三角形.这样的三角形共有个( 除外).
 12. 如图,在长方形网格中,每个小长方形的长为 ,宽为 , , 两点在网格格点上,若点 也在网格格点上,以 , , 为顶点的三角形的面积为 ,则满足条件的点 有个.
12. 如图,在长方形网格中,每个小长方形的长为 ,宽为 , , 两点在网格格点上,若点 也在网格格点上,以 , , 为顶点的三角形的面积为 ,则满足条件的点 有个.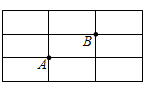 13. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.
13. 如图是5×5的正方形网格,△ABC的顶点都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形.画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画出个.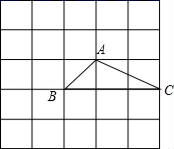 14. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)
14. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
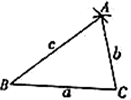 15. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .
15. 用直尺和圆规作△ABC,使BC=a,AC=b(a>b),∠B=30°,若这样的三角形能作两个,则a,b间满足的关系式是 .三、解答题
-
16. 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.(尺规作图,保留作图痕迹,不写作法)
 17. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(1,1),B(3,﹣3),C(4,3).
17. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(1,1),B(3,﹣3),C(4,3).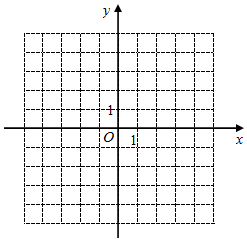
( 1 )在平面直角坐标系中标出A、B、C三点,画出△ABC;
( 2 )作出△ABC关于y轴的对称图形△A1B1C1 , 并写出A1、B1、C1三点坐标.
18.如图,等边△ABC和等边△ECD的边长相等,BC与CD在同一直线上,请根据如下要求,使用无刻度的直尺画图.
(1)在图①中画一个直角三角形;
(2)在图②中画出∠ACE的平分线.

四、综合题
-
19. 已知三点: , , .
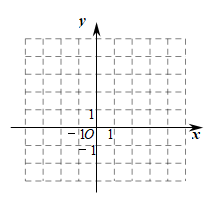 (1)、在所给的平面直角坐标系中画出;(2)、若C点与点关于x轴对称,求直线的函数表达式.20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)的顶点A,B的坐标分别为 , .
(1)、在所给的平面直角坐标系中画出;(2)、若C点与点关于x轴对称,求直线的函数表达式.20. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)的顶点A,B的坐标分别为 , .
⑴请在网格平面内画出平面直角坐标系;
⑵若点C的坐标为 , 请标出点C,并画出;
⑶请画出关于y轴对称的;
⑷直接写出的面积为 ▲ .
21. 如图,方格纸中的每个小方格都是边长为的正方形,在建立平面直角坐标系后,的顶点均在格点上,且坐标分别为 , , . (1)、画出关于轴对称的其中 , , 分别是 , , 的对应点,不写画法(2)、写出点 , , 的坐标(3)、求的面积.
(1)、画出关于轴对称的其中 , , 分别是 , , 的对应点,不写画法(2)、写出点 , , 的坐标(3)、求的面积.