北师大版2022-2023学年度第二学期七年级数学 认识三角形 期末复习
试卷更新日期:2023-05-15 类型:复习试卷
一、单选题
-
1. 要得知作业纸上两相交直线 , 所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图1和图2):

图 图
对于方案Ⅰ、Ⅱ,说法正确的是
 ( )A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行2. 已知三角形的三边长分别为3,5, , 则不可能是( )A、3 B、5 C、7 D、83. 如图,已知,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD.有下列结论:①AD∥BC;②∠ECD=∠DAC;③∠CEF=∠CFE;④CACE=∠ABC.其中正确的结论有( )
( )A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行2. 已知三角形的三边长分别为3,5, , 则不可能是( )A、3 B、5 C、7 D、83. 如图,已知,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD.有下列结论:①AD∥BC;②∠ECD=∠DAC;③∠CEF=∠CFE;④CACE=∠ABC.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个4. 如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )
A、1个 B、2个 C、3个 D、4个4. 如图,AB∥CD,点P在AB,CD之间,∠ACP=2∠PCD=40°,连结AP,若∠BAP=α,∠CAP=α+β.下列说法中正确的是( )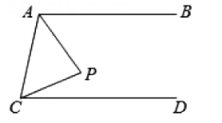 A、当∠P=60°时,α=30° B、当∠P=60°时,β=40° C、当=20°时,∠P=90° D、当β=0°时,∠P=90°5. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm6. 如图,三角板的直角顶点在直尺的一边上.若 , , 则的度数是( )
A、当∠P=60°时,α=30° B、当∠P=60°时,β=40° C、当=20°时,∠P=90° D、当β=0°时,∠P=90°5. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm6. 如图,三角板的直角顶点在直尺的一边上.若 , , 则的度数是( ) A、 B、 C、 D、7. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( )
A、 B、 C、 D、7. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( ) A、 B、 C、 D、8. 用一块含角的透明直角三角板画已知的边BC上的高,下列三角板的摆放位置正确的是( )A、
A、 B、 C、 D、8. 用一块含角的透明直角三角板画已知的边BC上的高,下列三角板的摆放位置正确的是( )A、 B、
B、 C、
C、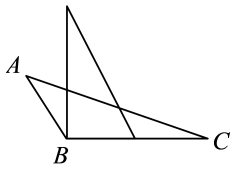 D、
D、 9. 如图,的两条角平分线 , 交于点P,若 , 则为( )
9. 如图,的两条角平分线 , 交于点P,若 , 则为( ) A、112° B、115° C、120° D、125°10. 如图,在中, , , BD平分 , 于点E,则的度数为( )
A、112° B、115° C、120° D、125°10. 如图,在中, , , BD平分 , 于点E,则的度数为( )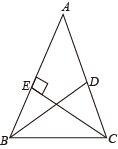 A、90° B、100° C、110° D、120°
A、90° B、100° C、110° D、120°二、填空题
-
11. 小明将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起,当 , 且点E在直线的上方时,他发现若 , 则三角板有一条边与斜边平行.
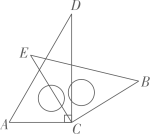 12. 若a,b,c是三角形的三边长,化简:.13. 如图,已知∠1=∠2,∠B=30°,则∠3=°.
12. 若a,b,c是三角形的三边长,化简:.13. 如图,已知∠1=∠2,∠B=30°,则∠3=°. 14. 如图消防云梯,其示意图如图1所示,其由救援台AB,延展臂BC(B在C的左侧)、伸展主臂CD,支撑臂EF构成,在作业过程中,救援台AB、车身GH及地面MN三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂BC与支摚臂EF所在直线互相垂直,且∠EFH=69°,则这时展角∠ABC= .
14. 如图消防云梯,其示意图如图1所示,其由救援台AB,延展臂BC(B在C的左侧)、伸展主臂CD,支撑臂EF构成,在作业过程中,救援台AB、车身GH及地面MN三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂BC与支摚臂EF所在直线互相垂直,且∠EFH=69°,则这时展角∠ABC= . 15. 如图,直线垂直于直线AB、分别交于点、 , , 直线、间存在、两点,使得、 , 与的角平分线相交于点 , , , 则.
15. 如图,直线垂直于直线AB、分别交于点、 , , 直线、间存在、两点,使得、 , 与的角平分线相交于点 , , , 则.
三、解答题
-
16. 如图,直线 , 平分 , , 垂足为点 , = , 求的度数.
 17. 已知:如图,在中, , , 点D,E分别在和上,且.求证: , 并写出最后一步推理的依据.
17. 已知:如图,在中, , , 点D,E分别在和上,且.求证: , 并写出最后一步推理的依据. 18. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.
18. 如图,在△ABC中,∠A= , ∠B= , CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.
四、综合题
-
19. 如图, , 直线分别交 , 于点G,H,是的平分线.
 (1)、如果为的平分线,试判断和的位置关系,请说明理由.(2)、如果是的平分线,(1)中的结论还成立吗?如果不成立,和有什么位置关系?请说明理由.20. 如图,AB∥CD,∠1=∠2.
(1)、如果为的平分线,试判断和的位置关系,请说明理由.(2)、如果是的平分线,(1)中的结论还成立吗?如果不成立,和有什么位置关系?请说明理由.20. 如图,AB∥CD,∠1=∠2. (1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.21. 如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2
(1)、试说明∠3=∠4;(2)、若∠BAD=∠BDA,且∠EBF=110°,求∠ADC的度数.21. 如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2 (1)、判断AD与BC是否平行,并说明理由;(2)、当∠A=∠C,∠1=50°时,求∠D的度数.
(1)、判断AD与BC是否平行,并说明理由;(2)、当∠A=∠C,∠1=50°时,求∠D的度数.

