北师大版2022-2023学年度第二学期七年级数学 探索直线平行的条件 期末复习
试卷更新日期：2023-05-15 类型：复习试卷
一、单选题
-
1. 如图，“因为∠2＝∠4，所以AD∥BC”，其推导的依据是（ ）
A、两直线平行，同位角相等 B、两直线平行，内错角相等 C、同位角相等，两直线平行 D、内错角相等，两直线平行 -
2. 如图所示，点在的延长线上，下列条件中能判断的是（ ）
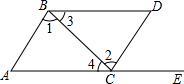A、 B、 C、 D、 -
3. 如图，下列条件中不能判定的是（ ）
A、 B、 C、 D、 -
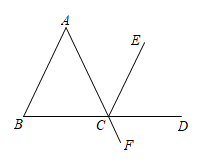
4. 如图，下列说法中不正确的是（ ）
A、和是同旁内角 B、和是内错角 C、和是同位角 D、和是对顶角 -
5. 仔细观察下列图形，其中∠1与∠2是内错角的是（ ）A、
B、
C、
D、
-
6. 如图所示，以下5个条件：①∠B=∠4+∠5；②∠2=∠4；③∠1=∠5；④∠B=∠3；⑤∠D+∠4+∠5= 180°．其中一定能判定AD∥BC的有（ ）
A、4个 B、3个 C、2个 D、1个 -
7. 如图，图中给出了过直线外一点作已知直线的平行线的方法，其依据的是（ ）
A、同平行于一条直线的两直线平行 B、同旁内角互补，两直线平行 C、内错角相等，两直线平行 D、同位角相等，两直线平行 -
8. 如图，下列条件能判断两直线和平行的是（ ）
A、 B、 C、 D、 -
9. 如图，若∠1=70°，∠2=110°，∠3=70°，则有（ ）．
A、a∥b B、c∥d C、a⊥d D、任两条都无法判定是否平行 -
10. 如图，已知 ， 则（ ）
A、 B、 C、 D、
二、填空题
-
11. 如图，请添加一个条件，使得 ， 则符合要求的其中一个条件可以是.
-
12. 如图，在图中标注的∠1、∠3、∠4、∠5中，当∠2 =∠时， AE∥BF.
-
13. 如图表示钉在一起的木条a，b，c．若测得∠1＝50°，∠2＝75°，要使木条a//b，木条a至少要旋转°．
-
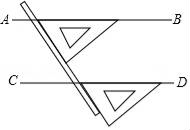
14. 如图，用直尺和三角尺作出直线AB、CD，得到AB∥CD的理由是 ．
-
15. 如图，下列错误的是（填序号）
①如果 ， 那么；②如果 ， 那么；
③如果 ， 那么；④如果 ， 那么；
⑤如果 ， 那么 ．
三、解答题
-
16. 已知：如图， ， 和互余，于点 ， 求证：.
-
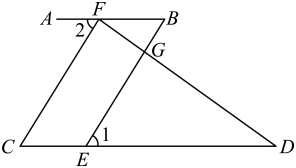
17. 如图AF 与BD相交于点C，∠B=∠ACB， 且CD平分∠ECF．求证： ．
请完成下列推理过程：
证明：∵CD 平分∠ECF
∴∠ECD= ▲ （ ）
∵∠ACB=∠FCD( ）
∴∠ECD=∠ACB( ）
∵∠B=∠ACB
∴∠B=∠▲（ ）
∴ （ ）．
-
18. 如图，直线 ， 被直线所截， ， ， 判断与是否平行，并说明理由.
四、综合题
-
19. 如图，直线CD、EF交于点O，OA，OB分别平分∠COE和∠DOE，且∠1+∠2=90°．
(1)、求证：AB∥CD；(2)、若∠2：∠3=25，求∠BOF的度数 -
20. 如图，B，F，E，C在同一条直线上，∠A＝∠D．
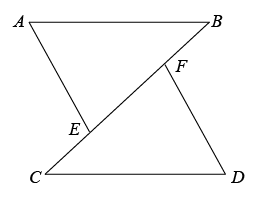(1)、若∠A＝78°，∠C＝47°，求∠BFD的度数．(2)、若∠AEB+∠BFD＝180°，求证：AB∥CD． -
21. 如图1，BD是△ABC的角平分线，作∠BDE = ∠ABD交AB于点E．
(1)、求证：ED∥BC；(2)、若AC⊥BD，点M为线段AC延长线上一点（不与点c重合），连接BM，若AB⊥BM，在图2中补全图形并证明：∠DBC = ∠BMA． -
22. 如图，B，F，E，C在同一条直线上，∠A＝∠D．
(1)、若∠A＝78°，∠C＝47°，求∠BFD的度数．(2)、若∠AEB+∠BFD＝180°，求证：AB∥CD． -
23. 如图，在中， ， 垂足为D，点E在上， ， 垂足为F．
(1)、求证：(2)、如果 ， 求证： ．
