北师大版2022-2023学年度第二学期七年级数学整式的除法期末复习

试卷更新日期：2023-05-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图1，将7张长为 $a$ ，宽为 $b (a > b)$ 的小长方形纸片，按图2的方式不重叠地放在矩形 $A B C D$ 内，未被覆盖的部分 $($ 两个矩形 $)$ 用阴影表示.设左上角与右下角的阴影部分的面积的差为 $S$ ，当 $B C$ 的长度变化时，按照同样的放置方式， $S$ 始终保持不变，则 $a$ ， $b$ 满足（）

A、 $a = b$ B、 $a = 3 b$ C、 $a = 2 b$ D、 $a = 4 b$

查看试题解析
2. 若定义表示xyz，表示 $4 a^{d} c^{b}$ ，则运算的结果为（）

A、 $2 m^{2} n$ B、 $4 m^{2} n$ C、 $2 m n^{2}$ D、 $4 m n^{2}$

查看试题解析
3. 如图，在长方形ABCD中，AB＝6，BC＝10，其内部有边长为a的正方形AEFG与边长为b的正方形HIJK，两个正方形的重合部分也为正方形，且面积为5，若S₂＝4S₁ ，则正方形AEFG与正方形HIJK的面积之和为（）

A、20 B、25 C、 $\frac{49}{2}$ D、 $\frac{81}{4}$

查看试题解析
4. 计算 $(- x^{5} + 3 x^{3} - M) \div (- 3 x) = \frac{1}{3} x^{4} - x^{2} + 2 x$ ，那么M=（）．

A、-3x B、 $3 x^{2}$ C、 $6 x^{2}$ D、 $- 6 x^{2}$

查看试题解析
5. 下列运算中，正确的是（）

A、 $x (3 x + 2) = 3 x^{2} + 2$ B、 $(2 x + y) (x^{3} + 1) = 2 x^{4} + y$ C、 $- 8 x^{5} y^{3} \div 2 x^{3} y = - 4 x^{2} y^{2}$ D、 $(6 x^{3} y - 3 x^{2} y^{2}) \div 3 x y = 2 x^{2} y - x y$

查看试题解析
6. 一个长方形的面积为 $3 x^{2} + 2 x$ ，它的一条边长为 $x$ ，则它的周长为（）

A、 $8 x + 4$ B、 $8 x + 2$ C、 $4 x + 2$ D、 $6 x + 4$

查看试题解析
7. 如图，根据计算长方形 $ABCD$ 的面积，可以说明下列等式成立的是（）

A、 ${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 ab + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $a (a + b) = a^{2} + ab$

查看试题解析
8. 若式子 $x^{2} + a x + 9 - {(x - 3)}^{2}$ 的值等于0，则a的值为（）

A、0 B、-3 C、-6 D、9

查看试题解析
9. 已知 $a \neq 0$ ，给出四个代数式，其中有一个代数式与其余代数式的化简结果不相等，则这个代数式是（）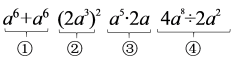

A、① B、② C、③ D、④

查看试题解析
10. 若M＝（x - 2）（x - 5），N＝（x - 2）（x - 6），则M与N的关系为（）

A、M＝N B、M＞N C、M＜N D、不能确定

查看试题解析

二、填空题

11. 我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式.例如图1可以得到 $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ，请解答下列问题：如图2，已知 $a + b + c = 12$ ， $a b + b c + a c = 38$ ，则 $a^{2} + b^{2} + c^{2}$ $=$ .

查看试题解析
12. 若长方形面积是 $2 a^{2} - 2 a b + 6 a$ ，一边长为 $2 a$ ，则这个长方形的另一边长是.

查看试题解析
13. 如图，5张长为a，宽为b(a>b)的小长方形纸片，不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示。设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，S始终保持不变，则a，b满足的关系是．

查看试题解析
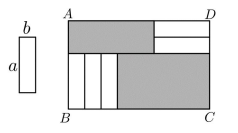14. 如图1，把3个边长为a的正方形和4个边长为b的小正方形，拼成一个长方形ABCD．把两个边长为b的小正方形放置在一个边长为a的大正方形中(如图2所示)．若图2阴影部分的面积比长方形ABCD的面积小81，则边长为a的正方形面积是

查看试题解析
15. 如图是一段T形钢材示意图，根据图中给出的尺寸，可计算其体积为．（用含a的代数式表示）

查看试题解析

三、解答题

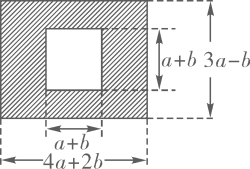
16. 广场内有一块边长为 $4 a m$ 的正方形花园，统一规划后，南北方向要缩短 $2 m$ ，东西方向要加长 $2 m$ .改造后的长方形花园的面积与原来的面积相比，是增加了还是减少了？增加或减少了多少平方米？

查看试题解析
17. 眉山市三苏雕像广场是为了纪念三苏父子而修建的．原是一块长为(4a+2b)米，宽为(3a-b)米的长方形地块，现在政府对广场进行改造，计划将如图四周阴影部分进行绿化，中间将保留边长为（a+b）米的正方形三苏父子雕像，则绿化的面积是多少平方米？并求出当a=20，b=10时的绿化面积．

查看试题解析
18. 某县学校分为初中部和小学部，做广播操时，两部分别站两个不同的操场上进行，站队时，做到了整齐划一，初中部排成的是一个规范的长方形方阵，每排 $(3 a - b)$ 人，站有 $(3 a + 2 b)$ 排；小学部站的方阵更特别，排数和每排人数都是 $2 (a + b)$ .试求：该县直学校初中部比小学部多多少名学生；

查看试题解析

四、综合题

19. 海伦是古希腊数学家，约公元62年左右活跃于亚历山大，年青时海伦酷爱数学，他的代表作《量度论》主要是研究面积、体积和几何分比问题，其中一段探究三角形面积的方法翻译如下：如图，设三角形面积为 $S$ ，以三角形各边为边向外作正方形，三个正方形的面积分别记作 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，定义： $\bar{S} = \frac{S_{1} + S_{2} + S_{3}}{2}$ ； ${S^{'}}_{1} = \bar{S} - S_{1}$ ； ${S^{'}}_{2} = \bar{S} - S_{2}$ ； ${S^{'}}_{3} = \bar{S} - S_{3}$ ； $F_{s} = {S^{'}}_{1} \times {S^{'}}_{2} + {S^{'}}_{2} \times {S^{'}}_{3} + {S^{'}}_{3} \times {S^{'}}_{1}$ ，经研究发现， $F_{s} = 4 S^{2}$ .如：三角形三条边分别为13、14、15，则 $S_{1} = 169$ ， $S_{2} = 196$ ， $S_{3} = 225$ ， $\bar{S} = 295$ ， ${S^{'}}_{1} = 126$ ； ${S^{'}}_{2} = 99$ ； $S_{3}^{^{'}} = 70$ ； $F_{s} = 28224$ ，所以 $S^{2} = 28224 \div 4 = 7056 = 8 4^{2}$ ，故三角形的面积 $S = 84$ .

(1)、若 $S_{1} = 3 ， S_{2} = 4 ， S_{3} = 5$ ，则 $\bar{S} =$ . $F_{s} =$ .

(2)、当 ${S^{'}}_{1} = x - 3$ ； ${S^{'}}_{2} = x + 3$ ； ${S^{'}}_{3} = 5 - x$ 时.
①求 $F_{s}$ 的表达式；
②若 $S_{1} + S_{2} + S_{3} = 20$ ，求三角形的面积.

查看试题解析
20. 如图所示，有-块边长为(3a+b)米和(a+2b) 米的长方形土地，现准备在这块土地上修建一个长为(2a+b)米，宽为(a+b)米的游泳池，剩余部分修建成休息区域．

(1)、请用含a和b的代数式表示休息区域的面积； (结果要化简)

(2)、若a=5，b=10，求休息区域的面积．

查看试题解析
21. 某公园有一块长为(4a+b)米，宽为(2a+b)米的长方形地块，规划部门计划其内部修建一座边长为(a+b)米的正方形雕像，左右两边修两条宽为a米的长方形道路，其余阴影部分进行为绿化场地，尺寸如图所示．

(1)、用含a，b的代数式表示绿化的面积是多少平方米(结果要化简)．

(2)、若a=3，b=2，请求出绿化面积．

查看试题解析
22. 已知关于x的多项式A，当 $A - {(x - 2)}^{2} = x (x + 7)$ 时，完成下列各小题.

(1)、求多项式A；

(2)、若 $3^{x + 1} = 1$ ，求多项式A的值.

查看试题解析
23. 观察下列各式：
$(x - 1) (x + 1) = x^{2} - 1$ ；
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；
……

(1)、根据以上规律，可知 $(x - 1) (x^{7} + x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1) =$ ；

(2)、你能否由此归纳出一般性规律： $(x - 1) (x^{n} + x^{n - 1} + \cdot \cdot \cdot + x + 1) =$ ；

(3)、根据（2）求出： $1 + 2 + 2^{2} + 2^{3} + \cdot \cdot \cdot + 2^{2022} + 2^{2023}$ .

查看试题解析

北师大版2022-2023学年度第二学期七年级数学 整式的除法 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期七年级数学整式的除法期末复习