北师大版2022-2023学年度第二学期七年级数学完全平方公式期末复习

试卷更新日期：2023-05-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知 $x - \frac{1}{x} = 4$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、6 B、16 C、14 D、18

查看试题解析
2. 下列计算正确的是（）

A、 $(- 2 x y)^{2} = - 4 x^{2} y^{2}$ B、 $(x - y)^{2} = x^{2} - y^{2}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 $2 x + 3 x = 5 x$

查看试题解析
3. 我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于 $a$ 的代数式 $A = a^{2} + a$ ，请结合你所学知识，判断下列说法正确的有（）个
①当 $a = - 3$ 时， $A = 6$ ；
②存在实数 $a$ ，使得 $A + \frac{1}{4} < 0$ ；
③若 $A - 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} = 3$ ；
④已知代数式 $A$ 、 $B$ 、 $C$ 满足 $A - B = 2 + \sqrt{2}$ ， $B - C = 2 - \sqrt{2}$ ，则 $A^{2} + B^{2} + C^{2} - A B - A C - B C = 14$ .

A、4 B、3 C、2 D、1

查看试题解析
4. 下列各式中，应用乘法公式计算正确的是（）

A、（x-y）（-y-x）＝y²-x² B、（2x-y）（y-2x）＝-y²-4x² C、（2a-1）²＝4a²-2a+1 D、（3-x）²＝9-x²

查看试题解析
5. 在下列各式：①a-b＝b-a；②（a-b）²＝（b-a）²；③（a-b）²＝-（b-a）²；④（a-b）³＝（b-a）³； ⑤（a+b）（a-b）＝（-a-b）（-a+b）中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ．若S₁＝2S₂ ，则a：b=（）

A、3：2 B、5：2 C、2：1 D、3：1

查看试题解析
7. 如图，边长为 $a 、 b$ 的长方形周长为12，面积为5，则 $a^{3} b + a b^{3}$ 的值为（）

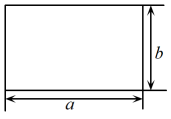A、60 B、120 C、130 D、240

查看试题解析
8. 若 $A ＝ x^{2} + 2 x - 6 y$ ， $B ＝ - y^{2} + 4 x - 11$ ，则A、B的大小关系为（）

A、A＞B B、A＜B C、A≥B D、A＝B

查看试题解析
9. 计算 $(a - b) (a + b) (a^{2} + b^{2}) (a^{4} - b^{4})$ 的结果是（）

A、 $a^{8} + 2 a^{4} b^{4} + b^{8}$ B、 $a^{8} - 2 a^{4} b^{4} + b^{8}$ C、 $a^{8} + b^{8}$ D、 $a^{8} - b^{8}$

查看试题解析
10. “数形结合”思想是一种常用的数学思想，其中“以形助数”是借助图形来理解和记忆数学公式．如图所示，将四张全等的长方形硬纸片围成一个正方形，根据图形面积的关系，可以直观地得到一个关于a、b的恒等式为（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = (a + b)^{2} - 4 a b$ D、 $a^{2} + a b = a (a + b)$

查看试题解析

二、填空题

11. 若M＝a²-ac+1，N＝ac-c² ，则M与N的大小关系是MN．

查看试题解析
12. 若 $a^{2} + 2 a - 2 = 0$ ，则 $(a + 1)^{2} =$ .

查看试题解析
13. 已知 ${(a + b)}^{2} = 16$ ， ${(a - b)}^{2} = 4$ ，则 $ab =$ ．

查看试题解析
14. 计算： $29 5^{2} + 10 \times 295 + 5^{2} =$

查看试题解析
15. 已知 $a - b = b - c = \frac{3}{5} ， a^{2} + b^{2} + c^{2} = 1$ ，则 $a b + b c + c a$ 的值等于．

查看试题解析

三、解答题

16. 阅读：已知a - b＝ -4，ab＝3，求a²+b²的值．小明的解法如下：
解：因为a - b＝ -4，ab＝3，
所以a² +b²＝（a - b）²+ 2ab＝（- 4）²+ 2×3＝22．
请你根据上述解题思路解答下面问题：
已知a - b＝ -5，ab＝2，求a²+ b²- ab的值．

查看试题解析
17. 已知：（x＋y）²＝35，（x-y）²＝15，分别求x²＋y²和xy的值．

查看试题解析
18. 已知： $x^{2} + y^{2} = 25 ， x + y = 7$ ，求2xy的值．

查看试题解析

四、综合题

19. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，请解答下列问题：

(1)、写出图2中所表示的数学等式.

(2)、根据整式乘法的运算法则，通过计算验证上述等式.

(3)、利用（1）中得到的结论，解决下面的问题：若 $a + b + c = 18$ ， $a^{2} + b^{2} + c^{2} = 116$ ，则 $a b + a c + b c =$ .

查看试题解析
20. 把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式.例如：由图1，可得等式： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ .

(1)、观察图2，请你写出 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 之间的一个恒等式： ${(a + b)}^{2} =$ ；

(2)、根据（1）的结论，若 ${(x + y)}^{2} = 12$ ， ${(x - y)}^{2} = 4$ ，求下列各式的值：
① $x y$ ；② $x^{2} + y^{2}$ .

查看试题解析
21. 通常，用两种不同的方法计算同一个图形的面积可以得到一个恒等式图将一个边长为 $a + b$ 的正方形图形分割成四部分（两个正方形和两个长方形），请观察图形，解答下列问题：

(1)、根据图中条件，用两种方法表示该图形的总面积，可得如下公式：；

(2)、如果图中的 $a$ 、 $b (a > b > 0)$ 满足 $a^{2} + b^{2} = 70$ ， $a b = 15$ ，求 $a + b$ 的值；

(3)、已知 $(x + 9)^{2} + (x - 1)^{2} = 124$ ，求 $(x + 9) (x - 1)$ .

查看试题解析
22. 如图 $1$ 是一个长为 $4 a$ ，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个如图 $2$ 的图形．

(1)、观察图形，请你写出 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的等量关系式；

(2)、若 $x + \frac{1}{x} = 3$ ，利用（1）中的结论，求 $x - \frac{1}{x}$ 的值；

(3)、若 $(2021 - m) (2022 - m) = 4$ ，求 $(m - 2021)^{2} + (2022 - m)^{2}$ 的值．

查看试题解析
23. 阅读下列材料：
我们知道对于二次三项式 $a^{2} + 2 a b + b^{2}$ 可以利用完全平方公式，将它变形为 ${(a + b)}^{2}$ 的形式．但是对于一般的二次三项式 $x^{2} + b x + c$ 就不能直接应用完全平方公式了，我们可以在二次三项式中先加上原式中一次项系数的一半的平方即 $(\frac{b}{2})^{2}$ ，使其凑成完全平方式，再减去 $(\frac{b}{2})^{2}$ ，使整个式子的值不变，这样就有 $x^{2} + b x + c = {(x + \frac{b}{2})}^{2} + m$ ．例如 $x^{2} - 6 x + 1$ ＝ $x^{2} - 6 x + 9 - 9 + 1$ ＝ ${(x - 3)}^{2} - 8$ ．
请根据上述材料解决下列问题：

(1)、将多项式 $x^{2} - 4 x + 3$ 变形为 $(x + m)^{2} + n$ 的形式；

(2)、当x，y分别取何值时 $x^{2} + y^{2} - 4 x + 6 y + 28$ 有最小值？求出这个最小值；

(3)、若 $m = a^{2} + b^{2} - 1$ ， $n = 2 a - 4 b - 7$ ，则m与n的大小关系是．

查看试题解析

北师大版2022-2023学年度第二学期七年级数学 完全平方公式 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期七年级数学完全平方公式期末复习