北师大版2022-2023学年度第二学期七年级数学平方差公式期末复习

试卷更新日期：2023-05-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各式能用平方差公式计算的是（）

A、 $(- a + b) (a - b)$ B、 $(a + b) (a - 2 b)$ C、 $(- x + 1) (x + 1)$ D、 $(- m - n) (m + n)$

查看试题解析
2. 若s+t=4，则s²-t²+8t的值是（）

A、8 B、12 C、16 D、32

查看试题解析
3. 如图在边长为a的正方形中挖掉一个边长为b的小正方形（ $a > b$ ）.把余下的部分前拼成一个矩形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - a b = a (a - b)$

查看试题解析
4. 计算(-6x-5y)(5y-6x)的结果是（）．

A、 $36 x^{2} - 25 y^{2}$ B、 $25 y^{2} - 36 x^{2}$ C、 $- 36 x^{2} - 25 y^{2}$ D、 $36 x^{2} + 25 y^{2}$

查看试题解析
5. 已知 $a^{2} - b^{2} = 32$ ， $a - b = 4$ 则 $a + b$ 的值是（）

A、2 B、4 C、6 D、8

查看试题解析
6. 若 $x + y = 3$ ， $x - y = 1$ ，则 $x^{2} - y^{2}$ 的值为（）

A、1 B、2 C、3 D、-3

查看试题解析
7. 如下图（1），边长为a的大正方形中一个边长为b的小正方形，小明将图（1）的阴影部分拼成了一个矩形，如图（2）．这一过程可以验证（）

A、a²+b²-2ab=(a-b)² B、a²+b²+2ab=(a+b)² C、2a²-3ab+b²=(2a-b)(a-b) D、a²-b²=(a+b) (a-b)

查看试题解析
8. 某同学粗心大意，分解因式时，把式子中的 $a^{4} - \oplus = (a^{2} - b) (a^{2} + b)$ 一部分弄污了，那么你认为式子中的 $\oplus$ 所对应的代数式是（）

A、 $b$ B、 $b^{2}$ C、 $2 b$ D、 $b^{4}$

查看试题解析
9. 如图1，将边长为a的正方形纸片，剪去一个边长为b的小正方形纸片，再沿着图1中的虚线剪开，把剪成的两部分（1）和（2）拼成如图2的平行四边形，这两个图能解释下列哪个等式（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $a^{2} + b^{2} = (a + b) (a - b)$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
10. 已知5⁴－1能被20~30之间的两个整数整除，则这两个整数是（）

A、25，27 B、26，28 C、24，26 D、22，24

查看试题解析

二、填空题

11. 已知a＝1²＋3²＋5²＋…＋25² ， b＝2²＋4²＋6²＋…＋24² ，则a－b的值为

查看试题解析
12. 计算：(2x-1)(2x+1)= ．

查看试题解析
13. 若 $a^{2} - b^{2} = 16$ ， $a - b = 8$ ，则 $a + b =$ ．

查看试题解析
14. 已知a²﹣4b²＝12，且a﹣2b＝﹣3，则a+2b＝．

查看试题解析
15. $3 (2^{2} + 1) (2^{4} + 1) \dots (2^{32} + 1) + 1$ 计算结果的个位数字是．

查看试题解析

三、解答题

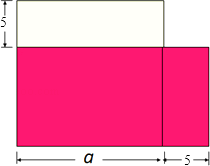
16. 已知a-b=30，b-c=25，且a²-c²=1650，求a+c的值.

查看试题解析
17. 如图所示，有一个狡猾的地主，把一块边长为a米的正方形土地租给马老汉栽种．过了一年，他对马老汉说：“我把你这块地的一边减少5米，另一边增加5米，继续租给你，你也没吃亏，你看如何？”马老汉一听，觉得好像没吃亏，就答应了．同学们，你们觉得马老汉有没有吃亏？请说明理由．

查看试题解析
18. 先化简，再求值：（2x+1）（2x﹣1）﹣3x（x+1）﹣（x﹣1）² ，当x=﹣1．

查看试题解析

四、综合题

19. 乘法公式的探究及应用.

(1)、如图1到图2的操作能验证的等式是____.（请选择正确的一个）

A、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ B、 $a^{2} + a b = a (a + b)$ C、 ${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

(2)、运用你所得到的公式，计算下列各题：
① $202 3^{2} - 2022 \times 2024$
②计算： $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) + 1$ .

查看试题解析
20. 公元3世纪，古希腊数学家丢番图（Diophantus）在其《算术》一书中设置了以下问题：已知两正整数之和为20，乘积为96，求这两个数．因为两数之和为20，所以这两个数不可能同时大于10，也不可能同时小于10，必定是一个大于10，一个小于10．根据如图所示的设法，可设一个数为 $10 + x$ ，则另一个数为 $10 - x$ ，根据两数之积为96，可得 $(10 + x) (10 - x) = 96$ ．请根据以上思路解决下列问题：

(1)、若两个正整数之和为100，大数比小数大 $2 a$ ，根据丢番图的设法，这两个正整数可表示为和；

(2)、请你根据丢番图的运算方法，计算 $502 \times 498$ 的值．

查看试题解析
21. 乘法公式的探究及应用．

(1)、如图，若将阴影部分裁剪下来，重新拼成一个长方形，面积是（写成多项式乘法的形式）

(2)、比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）．

(3)、运用你所得到的公式，计算下列各题：
① $10.3 \times 9.7$
② $(2 m + n - p) (2 m - n + p)$

查看试题解析
22. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形，1号正方形的边长为x，2号正方形的边长为y．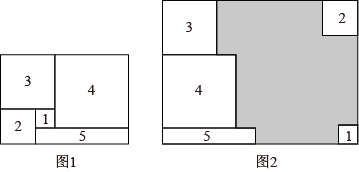

(1)、求5号长方形的面积（用含x，y的代数式表示）；

(2)、若图1中长方形的周长为24．
①若2号正方形与1号正方形的面积差为3，求5号长方形的面积；
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中，则没有覆盖的阴影部分的周长为 ▲ ．

查看试题解析
23. 在化简整式（x﹣2）■（x+2）+▲中，“■”表示运算符号“﹣”“×”中的某一个，“▲”表示一个整式．

(1)、计算（x﹣2）﹣（x+2）+（﹣5+y）；

(2)、若（x﹣2）（x+2）+▲＝3x²+6，求出整式“▲”；

(3)、若（x﹣2）■（x+2）+▲的计算结果是二次单项式，请直接写出一组满足条件的“■”及“▲”．

查看试题解析

北师大版2022-2023学年度第二学期七年级数学 平方差公式 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期七年级数学平方差公式期末复习