备考2023年中考数学压轴题训练 ——二次函数（7）

试卷更新日期：2023-05-14 类型：三轮冲刺

进入出卷网下载

一、真题

1. 如图，在平面直角坐标系中，抛物线y＝x²+bx+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（﹣1，0），点C的坐标为（0，﹣3）.

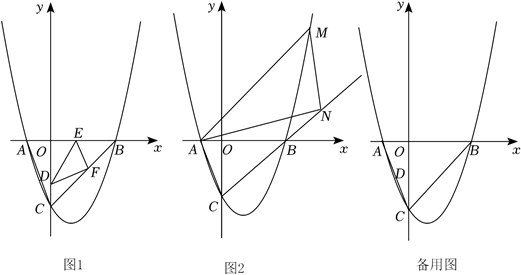(1)、求抛物线的解析式；

(2)、如图1，E为△ABC边AB上的一动点，F为BC边上的一动点，D点坐标为（0，﹣2），求△DEF周长的最小值；

(3)、如图2，N为射线CB上的一点，M是抛物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，若M到x轴的距离为d，△AMN面积为2d，当△AMN为等腰三角形时，求点N的坐标.

查看试题解析
2. 抛物线的解析式是 $y = - x^{2} + 4 x + a$ .直线 $y = - x + 2$ 与 $x$ 轴交于点 $M$ ，与 $y$ 轴交于点 $E$ ，点 $F$ 与直线上的点 $G (5 ， - 3)$ 关于 $x$ 轴对称.

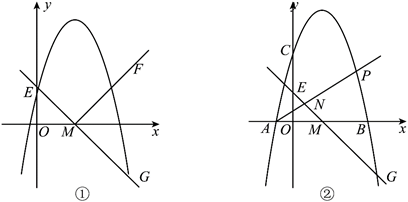(1)、如图①，求射线 $M F$ 的解析式；

(2)、在（1）的条件下，当抛物线与折线 $E M F$ 有两个交点时，设两个交点的横坐标是x₁ ， x₂（ $x_{1} < x_{2}$ ），求 $x_{1} + x_{2}$ 的值；

(3)、如图②，当抛物线经过点 $C (0 ， 5)$ 时，分别与 $x$ 轴交于 $A$ ， $B$ 两点，且点 $A$ 在点 $B$ 的左侧.在 $x$ 轴上方的抛物线上有一动点 $P$ ，设射线 $A P$ 与直线 $y = - x + 2$ 交于点 $N$ .求 $\frac{P N}{A N}$ 的最大值.

查看试题解析
3. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ .

(1)、若 $a = - 1$ ，且函数图象经过 $(0 ， 3)$ ， $(2 ， - 5)$ 两点，求此二次函数的解析式，直接写出抛物线与 $x$ 轴交点及顶点的坐标；

(2)、在图①中画出⑴中函数的大致图象，并根据图象写出函数值 $y \geq 3$ 时自变量 $x$ 的取值范围；

(3)、若 $a + b + c = 0$ 且 $a > b > c$ ，一元二次方程 $a x^{2} + b x + c = 0$ 两根之差等于 $a - c$ ，函数图象经过 $P (\frac{1}{2} - c ， y_{1}) ， Q (1 + 3 c ， y_{2})$ 两点，试比较 $y_{1} 、 y_{2}$ 的大小 .

查看试题解析
4. 在平面直角坐标系中，抛物线 $y = - x^{2} - 4 x + c$ 与 $x$ 轴交于点 $A$ ， $B$ （点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$ ，且点 $A$ 的坐标为 $(- 5 ， 0)$ .

(1)、求点 $C$ 的坐标；

(2)、如图1，若点 $P$ 是第二象限内抛物线上一动点，求点 $P$ 到直线 $A C$ 距离的最大值；

(3)、如图2，若点 $M$ 是抛物线上一点，点 $N$ 是抛物线对称轴上一点，是否存在点 $M$ 使以 $A$ ， $C$ ， $M$ ， $N$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $M$ 的坐标；若不存在，请说明理由.

查看试题解析
5. 如图1，已知二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象与x轴交于点 $A (- 1 ， 0)$ 、 $B (2 ， 0)$ ，与y轴交于点C，且 $t a n ∠ O A C = 2$ .

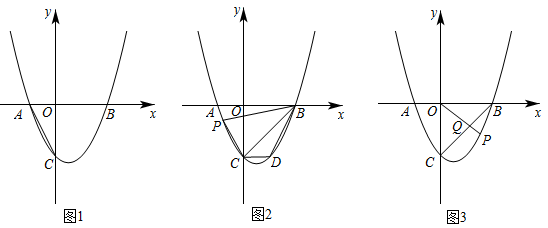(1)、求二次函数的解析式；

(2)、如图2，过点C作 $C D ∥ x$ 轴交二次函数图象于点D，P是二次函数图象上异于点D的一个动点，连接PB、PC，若 $S_{△ P B C} = S_{△ B C D}$ ，求点P的坐标；

(3)、如图3，若点P是二次函数图象上位于BC下方的一个动点，连接OP交BC于点Q.设点P的横坐标为t，试用含t的代数式表示 $\frac{P Q}{O Q}$ 的值，并求 $\frac{P Q}{O Q}$ 的最大值.

查看试题解析
6. 在平面直角坐标系中，直线y＝﹣x﹣2与x轴交于点A，与y轴交于点B，抛物线y＝ax²+bx+c（a＞0）经过A，B两点，并与x轴的正半轴交于点C.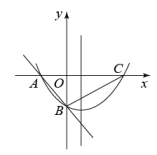

(1)、求a，b满足的关系式及c的值；

(2)、当a＝ $\frac{1}{4}$ 时，若点P是抛物线对称轴上的一个动点，求△PAB周长的最小值；

(3)、当a＝1时，若点Q是直线AB下方抛物线上的一个动点，过点Q作QD⊥AB于点D，当QD的值最大时，求此时点Q的坐标及QD的最大值.

查看试题解析
7. 如图1，在平面直角坐标系中，已知二次函数 $y = a x^{2} + b x + 2$ 的图象经过点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，与y轴交于点C.

(1)、求该二次函数的表达式；

(2)、连接 $B C$ ，在该二次函数图象上是否存在点P，使 $∠ P C B = ∠ A B C$ ？若存在，请求出点P的坐标：若不存在，请说明理由；

(3)、如图2，直线l为该二次函数图象的对称轴，交x轴于点E.若点Q为x轴上方二次函数图象上一动点，过点Q作直线 $A Q$ ， $B Q$ 分别交直线l于点M，N，在点Q的运动过程中， $E M + E N$ 的值是否为定值？若是，请求出该定值；若不是，请说明理由.

查看试题解析
8. 如图，抛物线 $y = a x^{2} + 2 x + c$ 的对称轴是直线 $x = 1$ ，与 $x$ 轴交于点 $A$ ， $B (3 ， 0)$ ，与 $y$ 轴交于点 $C$ ，连接 $A C$ .

(1)、求此抛物线的解析式；

(2)、已知点 $D$ 是第一象限内抛物线上的一个动点，过点 $D$ 作 $D M ⊥ x$ 轴，垂足为点 $M$ ， $D M$ 交直线 $B C$ 于点 $N$ ，是否存在这样的点 $N$ ，使得以 $A$ ， $C$ ， $N$ 为顶点的三角形是等腰三角形.若存在，请求出点 $N$ 的坐标，若不存在，请说明理由；

(3)、已知点 $E$ 是抛物线对称轴上的点，在坐标平面内是否存在点 $F$ ，使以点 $B$ 、 $C$ 、 $E$ 、 $F$ 为顶点的四边形为矩形，若存在，请直接写出点 $F$ 的坐标；若不存在，请说明理由.

查看试题解析
9. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A，B两点，与y轴交于点C，顶点为 $D (2 ， 1)$ ，抛物线的对称轴交直线 $B C$ 于点E.

(1)、求抛物线 $y = - x^{2} + b x + c$ 的表达式；

(2)、把上述抛物线沿它的对称轴向下平移，平移的距离为 $h (h > 0)$ ，在平移过程中，该抛物线与直线 $B C$ 始终有交点，求h的最大值；

(3)、M是（1）中抛物线上一点，N是直线 $B C$ 上一点.是否存在以点D，E，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由.

查看试题解析
10. 如图，在平面直角坐标系中，经过点 $A (4 ， 0)$ 的直线AB与y轴交于点 $B (0 ， 4)$ ．经过原点O的抛物线 $y = - x^{2} + b x + c$ 交直线AB于点A，C，抛物线的顶点为D．

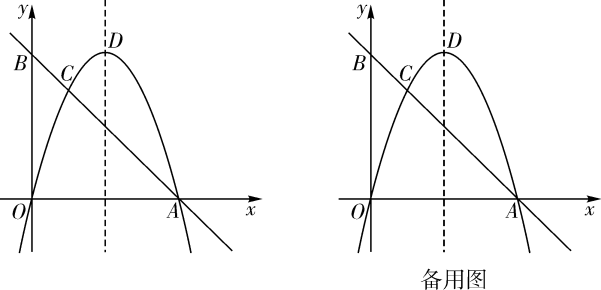(1)、求抛物线 $y = - x^{2} + b x + c$ 的表达式；

(2)、M是线段AB上一点，N是抛物线上一点，当 $M N ∥ y$ 轴且 $M N = 2$ 时，求点M的坐标；

(3)、P是抛物线上一动点，Q是平面直角坐标系内一点．是否存在以点A，C，P，Q为顶点的四边形是矩形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析
11. 在平面直角坐标系中，抛物线y＝﹣ $\frac{1}{2}$ $x^{2}$ ＋（m﹣1）x＋2m与x轴交于A，B（4，0）两点，与y轴交于点C，点P是抛物线在第一象限内的一个动点．

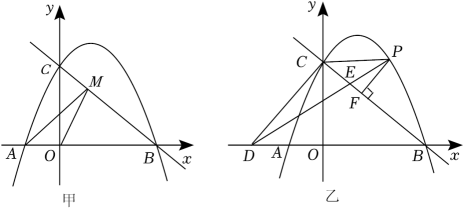(1)、求抛物线的解析式，并直接写出点A，C的坐标；

(2)、如图甲，点M是直线BC上的一个动点，连接AM，OM，是否存在点M使AM＋OM最小，若存在，请求出点M的坐标，若不存在，请说明理由；

(3)、如图乙，过点P作PF⊥BC，垂足为F，过点C作CD⊥BC，交x轴于点D，连接DP交BC于点E，连接CP．设△PEF的面积为S₁ ， △PEC的面积为S₂ ，是否存在点P，使得 $\frac{S_{1}}{S_{2}}$ 最大，若存在，请求出点P的坐标，若不存在，请说明理由．

查看试题解析
12. 如图1，在平面直角坐标系中，抛物线 $y = \frac{1}{4} (x + 3) (x - a)$ 与 $x$ 轴交于 $A$ ， $B (4 ， 0)$ 两点，点 $C$ 在 $y$ 轴上，且 $O C = O B$ ， $D$ ， $E$ 分别是线段 $A C$ ， $A B$ 上的动点（点 $D$ ， $E$ 不与点 $A$ ， $B$ ， $C$ 重合）.

(1)、求此抛物线的表达式；

(2)、连接 $D E$ 并延长交抛物线于点 $P$ ，当 $D E ⊥ x$ 轴，且 $A E = 1$ 时，求 $D P$ 的长；

(3)、连接 $B D$ .
①如图2，将 $△ B C D$ 沿 $x$ 轴翻折得到 $△ B F G$ ，当点 $G$ 在抛物线上时，求点 $G$ 的坐标；

②如图3，连接 $C E$ ，当 $C D = A E$ 时，求 $B D + C E$ 的最小值.

查看试题解析

二、模拟预测

13. 在平面直角坐标系 $x O y$ 中，抛物线 $L ： y = a x^{2} - 2 a x - 3 a (a > 0)$ 与x轴交于A，B两点（点A在点B的左侧），直线 $y = a x + 1$ 与抛物线交于C，D两点（点D在第一象限）．

(1)、如图，当点C与点A重合时，求抛物线的函数表达式；

(2)、在（1）的条件下，连接 $B D$ ，点E在抛物线上，若 $∠ D A E = ∠ A D B$ ，求出点E的坐标；

(3)、将抛物线L向上平移1个单位得到抛物线 $L_{1}$ ，抛物线 $L_{1}$ 的顶点为P，直线 $y = a x + 1$ 与抛物线 $L_{1}$ 交于M，N两点，连接 $M P ， N P$ ，若 $∠ M P N = 90 °$ ，求a的值．

查看试题解析
14. 如图，二次函数y＝-x²+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB＝OC，点D在函数图象上，CD∥x轴且CD＝2，直线l是抛物线的对称轴，E是抛物线的顶点.

(1)、求b、c的值；

(2)、如图1，连BE，线段OC上的点F关于直线l的对称点F′恰好在线段BE上，求点F的坐标；

(3)、如图2，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M、与抛物线交于点N.试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？若存在，求出点Q的坐标；若不存在，说明理由.

查看试题解析
15. 抛物线 $y = a x^{2} - 4$ 经过 $A$ 、 $B$ 两点，且 $O A = O B$ ，直线 $E C$ 过点 $E (4 ， - 1)$ ， $C (0 ， - 3)$ ，点 $D$ 是线段 $O A ($ 不含端点 $)$ 上的动点，过 $D$ 作 $P D ⊥ x$ 轴交抛物线于点 $P$ ，连接 $P C$ 、 $P E$ .

(1)、求抛物线与直线 $C E$ 的解析式；

(2)、求证： $P C + P D$ 为定值；

(3)、在第四象限内是否存在一点 $Q$ ，使得以 $C$ 、 $P$ 、 $E$ 、 $Q$ 为顶点的平行四边形面积最大，若存在，求出 $Q$ 点坐标；若不存在，请说明理由.

查看试题解析
16. 如图，抛物线y＝ax²+bx+c经过A（-6，0），OA＝3OB＝ $\frac{3}{2}$ OC，D为线段AC下方抛物线上一动点，过点D做DG⊥AC于G.

(1)、求抛物线的函数表达式；

(2)、求△ACD面积的最大值；

(3)、连接BC，是否存在点D，使得△CDG中有一个角与∠BCO相等？若存在，请求出点D的横坐标；若不存在，请说明理由.

查看试题解析
17. 已知抛物线经过原点，交x轴于点A，抛物线上一点B，直线 $y = \sqrt{3} x - \sqrt{3}$ 交x轴于点C，交y轴于点D，若 $A (10 ， 0)$ ， $B (2 ， 6)$ ， P为 $y = \sqrt{3} x - \sqrt{3}$ 上的一动点.

(1)、求抛物线的解析式；

(2)、P在第一象限，且在抛物线内，设点P的横坐标为 $O E = x$ .
（ⅰ）若直线与抛物线交于点 $D^{'}$ ，作 $D^{'} E ⊥ x$ 轴，求 $P D^{'} + 2 E P$ 的值（用x的代数式表示）；
（ⅱ）F在y轴的正半轴上，且 $O D = O F$ .连接 $C F$ ，直线 $B P$ 交x轴于点H，交y轴于点G，过点P作 $P I ∥ C F$ 交x轴于点I，过点I作y轴的平行线交于点J，连接 $C J$ ，过点I作 $I Q ∥ C J$ ，交 $G H$ 于点Q， $∠ C J I$ 的角平分线交x轴于点M，过点M作 $M L ∥ C J$ ，交 $J I$ 于点L，过点L作 $L N ⊥ C J$ 于点N，若 $J N + L M = I Q$ ，求点P的坐标.

查看试题解析
18. 抛物线 $y = - \frac{3}{8} x^{2} + b x + c (b > 0)$ 与x轴分别交于 $A$ ， $B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C (0 ， 3)$ ，抛物线对称轴为 $x = 1$ ，点 $Р$ 是第一象限抛物线上动点，连接 $B C$ ， $P B$ .

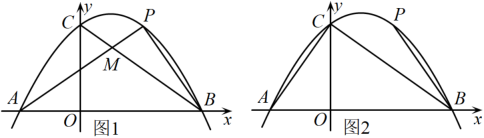(1)、求抛物线和直线 $B C$ 的解析式；

(2)、如图1，连接 $P A$ ，交 $B C$ 于点 $M$ ，设 $△ A B M$ 的面积为 $S_{1}$ ， $△ P B M$ 的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的最小值及此时点 $P$ 的坐标；

(3)、如图2，设 $∠ C B A = θ$ ，在直线 $B C$ 上方的抛物线上是否存在点 $P$ ，使得 $∠ P B C$ 恰好等于 $\frac{θ}{2}$ ，若存在，求出点 $P$ 的横坐标；若不存在，请说明理由.

查看试题解析
19. 如图，在直角坐标系中，直线 $y = \frac{1}{3} x + 1$ 与 $x$ 轴、 $y$ 轴的交点分别为 $A$ 、 $B$ ，以 $x = - 1$ 为对称轴的抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴分别交于点 $A$ 、 $C$ .

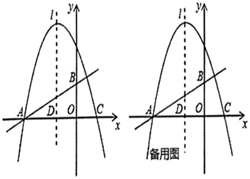(1)、求抛物线的解析式；

(2)、若点 $P$ 是第二象限内抛物线上的动点，其横坐标为 $t$ .设抛物线的对称轴 $l$ 与 $x$ 轴交于点 $D$ ，连接 $P D$ ，交 $A B$ 于 $E$ ，求出当以 $A$ 、 $D$ 、 $E$ 为顶点的三角形与 $Δ A O B$ 相似时点 $P$ 的坐标；

(3)、点 $M$ 是对称轴上任意一点，在抛物线上是否存在点 $N$ ，使以点 $A$ 、 $B$ 、 $M$ 、 $N$ 为顶点的四边形是平行四边形？若存在，请直接写出点 $N$ 的坐标；若不存在，说明理由.

查看试题解析
20. 如图，已知抛物线y＝ $\frac{1}{3} x^{2}$ +bx+c经过△ABC的三个顶点，其中点A（0，1），点B（-9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．

(1)、求抛物线的解析式；

(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点 E、F，当四边形AECP的面积最大时，求点P的坐标；

(3)、当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

查看试题解析