备考2023年中考数学压轴题训练 ——二次函数（6）

试卷更新日期：2023-05-14 类型：三轮冲刺

进入出卷网下载

一、真题

1. 如图，已知直线y=2x+2与抛物线y=ax²+bx+c相交于A，B两点，点A在x轴上，点B在y轴上，点C(3，0)在抛物线上.

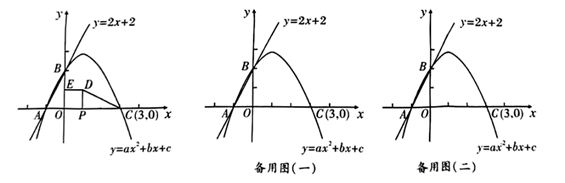(1)、求该抛物线的表达式.

(2)、正方形OPDE的顶点O为直角坐标系原点，顶点P在线段OC上，顶点E在y轴正半轴上，若△AOB与△DPC全等，求点P的坐标.

(3)、在条件（2）下，点Q是线段CD上的动点（点Q不与点D重合），将△PQD沿PQ所在的直线翻折得到△PQD'，连接CD'，求线段CD'长度的最小值.

查看试题解析
2. 如图1，在平面直角坐标系 $x O y$ 中，抛物线 $F_{1}$ ： $y = x^{2} + b x + c$ 经过点 $A (- 3 ， 0)$ 和点 $B (1 ， 0)$ .

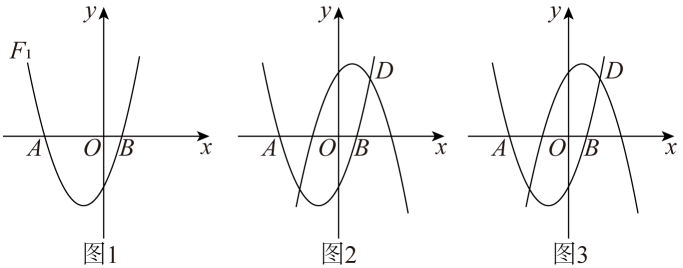(1)、求抛物线 $F_{1}$ 的解析式；

(2)、如图2，作抛物线 $F_{2}$ ，使它与抛物线 $F_{1}$ 关于原点 $O$ 成中心对称，请直接写出抛物线 $F_{2}$ 的解析式；

(3)、如图3，将（2）中抛物线 $F_{2}$ 向上平移2个单位，得到抛物线 $F_{3}$ ，抛物线 $F_{1}$ 与抛物线 $F_{3}$ 相交于 $C$ ， $D$ 两点（点 $C$ 在点 $D$ 的左侧）.
①求点 $C$ 和点 $D$ 的坐标；

②若点 $M$ ， $N$ 分别为抛物线 $F_{1}$ 和抛物线 $F_{3}$ 上 $C$ ， $D$ 之间的动点（点 $M$ ， $N$ 与点 $C$ ， $D$ 不重合），试求四边形 $C M D N$ 面积的最大值.

查看试题解析
3. 阅读材料：十六世纪的法国数学家弗朗索瓦·韦达发现了一元二次方程的根与系数之间的关系，可表述为“当判别式 $△ \geq 0$ 时，关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个根 $x_{1}$ 、 $x_{2}$ 有如下关系： $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} x_{2} = \frac{c}{a}$ ”.此关系通常被称为“韦达定理”.已知二次函数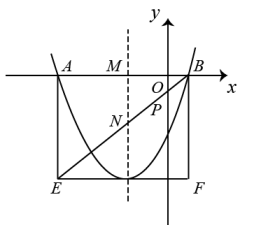 $y = a x^{2} + b x + c (a > 0)$ .

(1)、若 $a = 1$ ， $b = 3$ ，且该二次函数的图象过点 $(1 ， 1)$ ，求 $c$ 的值；

(2)、如图所示，在平面直角坐标系 $O x y$ 中，该二次函数的图象与 $x$ 轴相交于不同的两点 $A (x_{1} ， 0)$ 、 $B (x_{2} ， 0)$ ，其中 $x_{1} < 0 < x_{2}$ 、 $| x_{1} | > | x_{2} |$ ，且该二次函数的图象的顶点在矩形 $A B F E$ 的边 $E F$ 上，其对称轴与 $x$ 轴、 $B E$ 分别交于点 $M$ 、 $N$ ， $B E$ 与 $y$ 轴相交于点 $P$ ，且满足 $t a n ∠ A B E = \frac{3}{4}$ .
①求关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 的根的判别式的值；
②若 $N P = 2 B P$ ，令 $T = \frac{1}{a^{2}} + \frac{16}{5} c$ ，求 $T$ 的最小值.

查看试题解析
4. 若关于x的函数y，当 $t - \frac{1}{2} \leq x \leq t + \frac{1}{2}$ 时，函数y的最大值为M，最小值为N，令函数 $h = \frac{M - N}{2}$ ，我们不妨把函数h称之为函数y的“共同体函数”.

(1)、①若函数 $y = 4044 x$ ，当 $t = 1$ 时，求函数y的“共同体函数”h的值；
②若函数 $y = k x + b$ （ $k \neq 0$ ， k，b为常数），求函数y的“共同体函数”h的解析式；

(2)、若函数 $y = \frac{2}{x} （ x \geq 1 ）$ ，求函数y的“共同体函数”h的最大值；

(3)、若函数 $y = - x^{2} + 4 x + k$ ，是否存在实数k，使得函数y的最大值等于函数y的“共同体函数”h的最小值.若存在，求出k的值；若不存在，请说明理由.

查看试题解析
5. 如图一所示，在平面直角坐标中，抛物线y＝ax²+2x+c经过点A(﹣1，0）、B（3，0），与y轴交于点C，顶点为点D.在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PF $∥$ AB交BC于点F.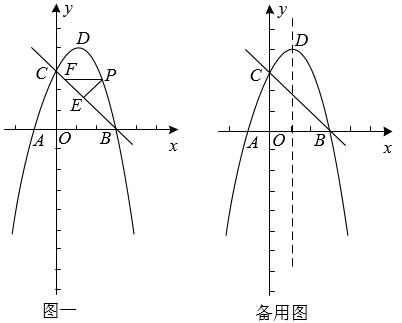

(1)、求抛物线和直线BC的函数表达式，

(2)、当△PEF的周长为最大值时，求点P的坐标和△PEF的周长.

(3)、若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由.

查看试题解析
6. 已知抛物线y＝x²+bx+c．

(1)、如图①，若抛物线图象与x轴交于点A（3，0），与y轴交点B（0，﹣3），连接AB.
（Ⅰ）求该抛物线所表示的二次函数表达式；

（Ⅱ）若点P是抛物线上一动点（与点A不重合），过点P作PH⊥x轴于点H，与线段AB交于点M，是否存在点P使得点M是线段PH的三等分点？若存在，请求出点P的坐标：若不存在，请说明理由.

(2)、如图②，直线y＝ $\frac{4}{3}$ x+n与y轴交于点C，同时与抛物线y=x²+bx+c交于点D（﹣3，0），以线段CD为边作菱形CDFE，使点F落在x轴的正半轴上，若该抛物线与线段CE没有交点，求b的取值范围.

查看试题解析
7. 已知关于 $x$ 的函数 $y = a x^{2} + b x + c$ .

(1)、若 $a = 1$ ，函数的图象经过点 $(1 ， - 4)$ 和点 $(2 ， 1)$ ，求该函数的表达式和最小值；

(2)、若 $a = 1$ ， $b = - 2$ ， $c = m + 1$ 时，函数的图象与 $x$ 轴有交点，求 $m$ 的取值范围.

(3)、阅读下面材料：
设 $a > 0$ ，函数图象与 $x$ 轴有两个不同的交点 $A$ ， $B$ ，若 $A$ ， $B$ 两点均在原点左侧，探究系数 $a$ ， $b$ ， $c$ 应满足的条件，根据函数图象，思考以下三个方面：

①因为函数的图象与 $x$ 轴有两个不同的交点，所以 $Δ = b^{2} - 4 a c > 0$ ；

②因为 $A$ ， $B$ 两点在原点左侧，所以 $x = 0$ 对应图象上的点在 $x$ 轴上方，即 $c > 0$ ；

③上述两个条件还不能确保 $A$ ， $B$ 两点均在原点左侧，我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置：即需 $- \frac{b}{2 a} < 0$ .

综上所述，系数 $a$ ， $b$ ， $c$ 应满足的条件可归纳为： ${\begin{array}{l} a > 0 \\ Δ = b^{2} - 4 a c > 0 \\ c > 0 \\ - \frac{b}{2 a} < 0 \end{array}$

请根据上面阅读材料，类比解决下面问题：

若函数 $y = a x^{2} - 2 x + 3$ 的图象在直线 $x = 1$ 的右侧与 $x$ 轴有且只有一个交点，求 $a$ 的取值范围.

查看试题解析
8. 如图，抛物线 $y = \frac{1}{2} x^{2} - 2 x - 6$ 与 $x$ 轴相交于点 $A$ 、点 $B$ ，与 $y$ 轴相交于点 $C$ .

(1)、请直接写出点 $A$ ， $B$ ， $C$ 的坐标；

(2)、点 $P (m ， n) (0 < m < 6)$ 在抛物线上，当 $m$ 取何值时， $△ P B C$ 的面积最大？并求出 $△ P B C$ 面积的最大值.

(3)、点 $F$ 是抛物线上的动点，作 $F E$ // $A C$ 交 $x$ 轴于点 $E$ ，是否存在点 $F$ ，使得以 $A$ 、 $C$ 、 $E$ 、 $F$ 为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点 $F$ 的坐标；若不存在，请说明理由.

查看试题解析
9. 已知抛物线 $y = x^{2} + b x + c$ 与x轴相交于点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，与y轴相交于点C.

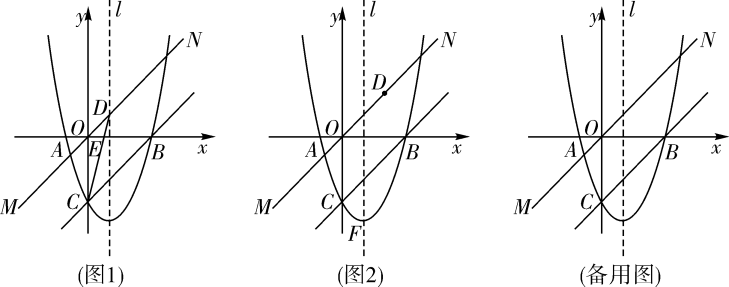(1)、求抛物线的表达式；

(2)、如图1，将直线BC间上平移，得到过原点O的直线MN.点D是直线MN上任意一点.
①当点D在抛物线的对称轴l上时，连接CD，关x轴相交于点E，求线段OE的长；

②如图2，在抛物线的对称轴l上是否存在点F，使得以B，C，D，F为顶点的四边形是平行四边形？若存在，求出点F与点D的坐标；若不存在，请说明理由.

查看试题解析
10. 定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”，如图①，抛物线C₁：y＝x²+2x﹣3与抛物线C₂：y＝ax²+2ax+c组成一个开口向上的“月牙线”，抛物线C₁和抛物线C₂与x轴有着相同的交点A（﹣3，0）、B（点B在点A右侧），与y轴的交点分别为G、H（0，﹣1）．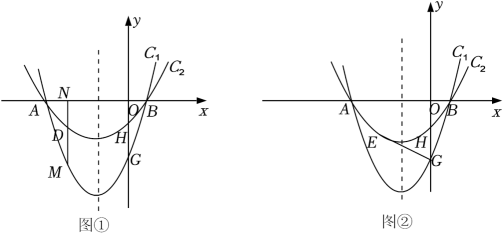

(1)、求抛物线C₂的解析式和点G的坐标．

(2)、点M是x轴下方抛物线C₁上的点，过点M作MN⊥x轴于点N，交抛物线C₂于点D，求线段MN与线段DM的长度的比值．

(3)、如图②，点E是点H关于抛物线对称轴的对称点，连接EG，在x轴上是否存在点F，使得△EFG是以EG为腰的等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由．

查看试题解析

二、模拟预测

11. 综合与探究：如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 4$ 与x轴交于点 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ，与y轴交于点C，连接 $B C$ .若在第四象限的抛物线上取一点M，过点M作 $M D ⊥ x$ 轴于点D，交直线 $B C$ 于点E.

(1)、求抛物线的表达式；

(2)、试探究抛物线上是否存在点M，使 $M E$ 有最大值？若存在，求出点M的坐标和 $M E$ 的最大值；若不存在，请说明理由；

(3)、连接 $C M$ ，试探究是否存在点M，使得以M，C，E为顶点的三角形和 $△ B D E$ 相似？若存在，请求出点M的坐标；若不存在，请说明理由.

查看试题解析
12. 如图，抛物线 $y = \frac{1}{2} x^{2} - 2 x - 6$ 与x轴相交于点A、点B，与y轴相交于点C.

(1)、请直接写出点A，B，C的坐标；

(2)、若点P是抛物线 $B C$ 段上的一点，当 $△ P B C$ 的面积最大时求出点P的坐标，并求出 $△ P B C$ 面积的最大值.

(3)、点F是抛物线上的动点，作 $F E ∥ A C$ 交x轴于点E，是否存在点F，使得以A、C、E、F为顶点的四边形是平行四边形？若存在，请写出所有符合条件的点F的坐标；若不存在，请说明理由.

查看试题解析
13. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + b x + 8$ 与x轴交于点A，B，与y轴交于点C，直线 $y = x - t$ 过点B，与y轴交于点D，点C与点D关于x轴对称.点P是线段 $O B$ 上一动点，过点P作x轴的垂线交抛物线于点M，交直线 $B D$ 于点N.

(1)、求抛物线的解析式；

(2)、当 $△ M D B$ 的面积最大时，求点P的坐标；

(3)、在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N，D为顶点的四边形是平行四边形，若存在，求出点Q的坐标；若不存在；说明理由

查看试题解析
14. 如图，在平面直角坐标系中，直线 $y = - 2 x + 10$ 与x轴、y轴相交于A、B两点，点C的坐标是 $(8 ， 4)$ ，连接 $A C 、 B C$ .

(1)、求过O、A、C三点的抛物线的解析式；

(2)、求证： $△ A O B ≌ △ A C B$ ；

(3)、动点P从点O出发，沿 $O B$ 以每秒2个单位长度的速度向点B运动；同时，动点Q从点B出发，沿 $B C$ 以每秒1个单位长度的速度向点C运动.规定其中一个动点到达终点时，另一个动点也随之停止运动.设运动时间为t秒，当t为何值时， $P A = Q A$ ？

查看试题解析
15. 如图，直线y＝﹣ $\frac{3}{4}$ x+3与x轴交于点A，与y轴交于点B，抛物线y＝ax²+ $\frac{3}{4}$ x+c经过A、B两点.

(1)、求二次函数解析式；

(2)、如图1，点E在线段AB上方的抛物线上运动（不与A、B重合），过点E作ED⊥AB，交AB于点D，作EF⊥AC，交AC于点F，交AB于点M，求△DEM的周长的最大值；

(3)、在（2）的结论下，连接CM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、C、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.

(4)、如图2，点N的坐标是（1，0），将线段ON绕点O逆时针旋转得到ON′，旋转角为α（0°＜α＜90°），连接N′A、N′B，求N′A+ $\frac{1}{3}$ N′B的最小值.

查看试题解析
16. 如图，抛物线y＝-x²+bx+c与x轴交于点A（1，0）和点B（-3，0），与y轴交于点C.

(1)、求b，c的值；

(2)、如图1，点P为直线BC上方抛物线上的一个动点，设点P的横坐标m.当m为何值时，△PBC的面积最大？并求出这个面积的最大值.

(3)、如图2，将该抛物线向左平移2个单位长度得到新的抛物线y＝a₁x²+b₁x+c₁（a₁≠0），平移后的抛物线与原抛物线相交于点D，点M为直线BC上的一点，点N是平面坐标系内一点，是否存在点M，N，使以点B，D，M，N为顶点的四边形为菱形，若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析
17. 已知：二次函数 $y = a x^{2} - 2 x + c$ 的图象与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，对称轴是直线 $x = 1$ ，且图象向右平移一个单位后经过坐标原点O，

(1)、求这个二次函数的解析式；

(2)、直线 $y = - \frac{1}{3} x + 1$ 交y轴于D点，E为抛物线顶点.若 $∠ D B C = α$ ， $∠ C B E = β$ ，求 $α - β$ 的值.

(3)、在（2）问的前提下，P为抛物线对称轴上一点，且满足 $P A = P C$ ，在y轴右侧的抛物线上是否存在点M，使得 $△ B D M$ 的面积等于 $P A^{2}$ ，若存在，求出点M的坐标；若不存在，请说明理由.

查看试题解析
18. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c (a c \neq 0)$ 与x轴交于点A和点B（点A在点B的左侧），与y轴交于点C.若线段 $O A 、 O B 、 O C$ 的长满足 $O C^{2} = O A \cdot O B$ ，则这样的抛物线称为“黄金”抛物线.如图，抛物线 $y = a x^{2} + b x + 2 (a \neq 0)$ 为“黄金”抛物线，其与x轴交点为A，B（其中B在A的右侧），与y轴交于点C.且 $O A = 4 O B$

(1)、求抛物线的解析式；

(2)、若P为 $A C$ 上方抛物线上的动点，过点P作 $P D ⊥ A C$ ，垂足为D.
①求 $P D$ 的最大值；

②连接 $P C$ ，当 $△ P C D$ 与 $△ A C O$ 相似时，求点P的坐标.

查看试题解析
19. 在平面直角坐标系中，点O为坐标原点，抛物线 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ 交x轴的负半轴于点A，交x轴的正半轴于点B，交y轴的正半轴于点C，且OB=2OC.

(1)、求点B的坐标和a的值；

(2)、如图1，点D，P分别在一、三象限的抛物线上，其中点P的横坐标为t，连接BP，交y轴于点E，连接CD，DE，设△CDE的面积为s，若 $s = - \frac{3}{4} t$ ，求点D的坐标；

(3)、如图2，在（2）的条件下，将线段DE绕点D逆时针旋转90°得到线段DF，射线AE与射线FB交于点G，连接AP，若∠AGB=2∠APB，求点P的坐标.

查看试题解析
20. 已知抛物线与 $x$ 轴交于点 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ ，与 $y$ 轴交于点 $C (0 ， 3)$ .

(1)、求抛物线解析式；

(2)、如图①，若点 $P$ 是第一象限内抛物线上一动点，过点 $P$ 作 $P D ⊥ B C$ 于点 $D$ ，求线段 $P D$ 长的最大值

(3)、如图②，若点 $N$ 是抛物线上另一动点，点 $M$ 是平面内一点，是否存在以点 $B$ 、 $C$ 、 $M$ 、 $N$ 为顶点，且以 $B C$ 为边的矩形，若存在，求出点 $M$ 的坐标；若不存在，请说明理由

查看试题解析
21. 如图，在平面直角坐标系中，抛物线（a＜0）与x轴交于A（-2，0）、B（4，0）两点，与y轴交于点C，且OC＝2OA．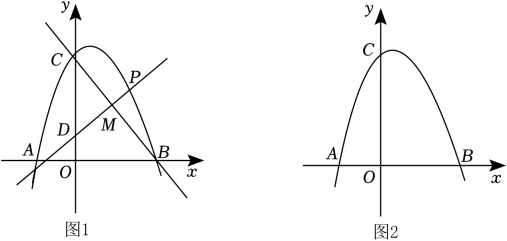

(1)、试求抛物线的解析式；

(2)、直线y＝kx+1（k＞0）与y轴交于点D，与抛物线交于点P，与直线BC交于点M，记m＝ $\frac{P M}{D M}$ ，试求m的最大值及此时点P的坐标：

(3)、连接AC，抛物线上是否存在点Q，使得∠BAQ＝2∠OCA？如果存在，请求出点Q的坐标；如果不存在，请说明理由．

查看试题解析
22. 规定：如果两个函数图象上至少存在一对点是关于原点对称的，我们则称这两个函数互为“守望函数”，这对点称为“守望点”．例如：点P（2，4）在函数 $y = x^{2}$ 上，点Q（ $- 2$ ， $- 4$ ）在函数 $y = - 2 x - 8$ 上，点P与点Q关于原点对称，此时函数 $y = x^{2}$ 和 $y = - 2 x - 8$ 互为“守望函数”，点P与点Q则为一对“守望点”．

(1)、函数 $y = - 2 x - 1$ 和函数 $y = 4 x$ 是否互为“守望函数”？若是，求出它们的“守望点”，若不是，请说明理由；

(2)、已知函数 $y = x^{2} + 2 x$ 和 $y = 4 x + n - 2022$ 互为“守望函数”，求n的最大值并写出取最大值时对应的“守望点”；

(3)、已知二次函数 $y = a x^{2} + b x + c$ $(a > 0)$ 与 $y = 2 b x + 1$ 互为“守望函数”，有且仅有一对“守望点”，若二次函数的顶点为M，与x轴交于 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ，其中 $0 < x_{1} < x_{2}$ ， $A B = 2$ ，又 $a = \frac{4 c}{c^{2} - c + 6}$ ，过顶点M作x轴的平行线l交y轴于点N，直线 $y = 2 b x + 1$ 与y轴交点为点Q，动点E在x轴上运动，求抛物线 $y = a x^{2} + b x + c$ $(a > 0)$ 上的一点F的坐标，使得四边形 $F Q E N$ 为平行四边形．

查看试题解析